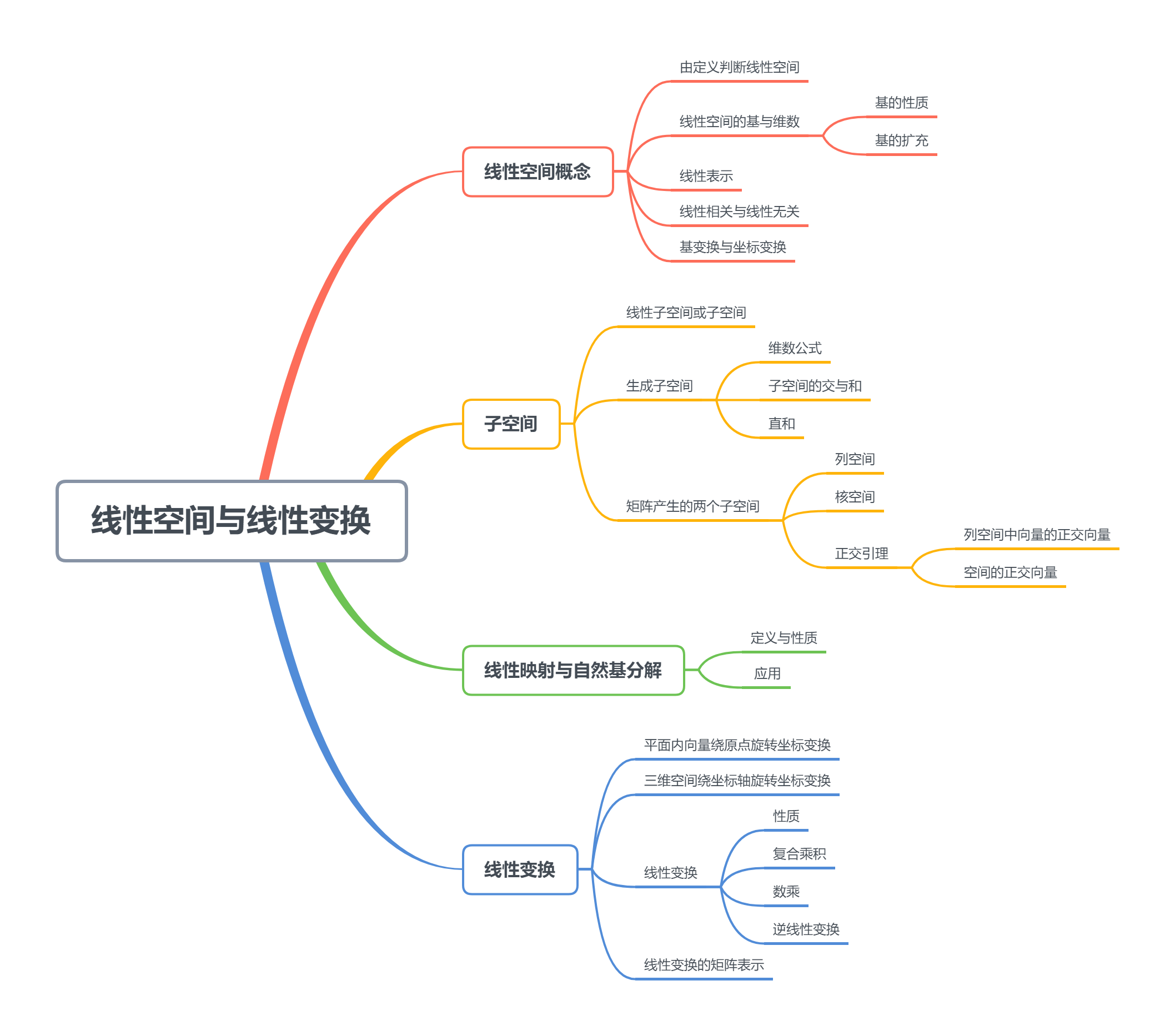
5.线性空间与线性变换

从本质上讲,人工智能的目标就是最优化——在复杂环境中与多体交互中做出最优决策
几乎所有的人工智能问题都会归结为一个优化问题
随着联结主义学派的兴起,概率统计已经取代了数理逻辑,成为了人工智能研究的主流工具
数理统计的关注点是 无处不在的可能性
频率学派认为先验分布式固定的,模型参数靠最大似然估计计算
贝叶斯学派认为先验分布是随机的,模型参数靠后验概率最大化计算
数理统计的任务是根据可观察的样本反过来推断总体的性质
推断的工具是统计量,统计量是样本的函数,是个随机变量
参数估计通过随机抽取的样本来估计总体分布的未知参数,包括点估计和区间估计
假设检验通过随机抽取的样本来接收或拒绝关于总体的某个判断
参考:
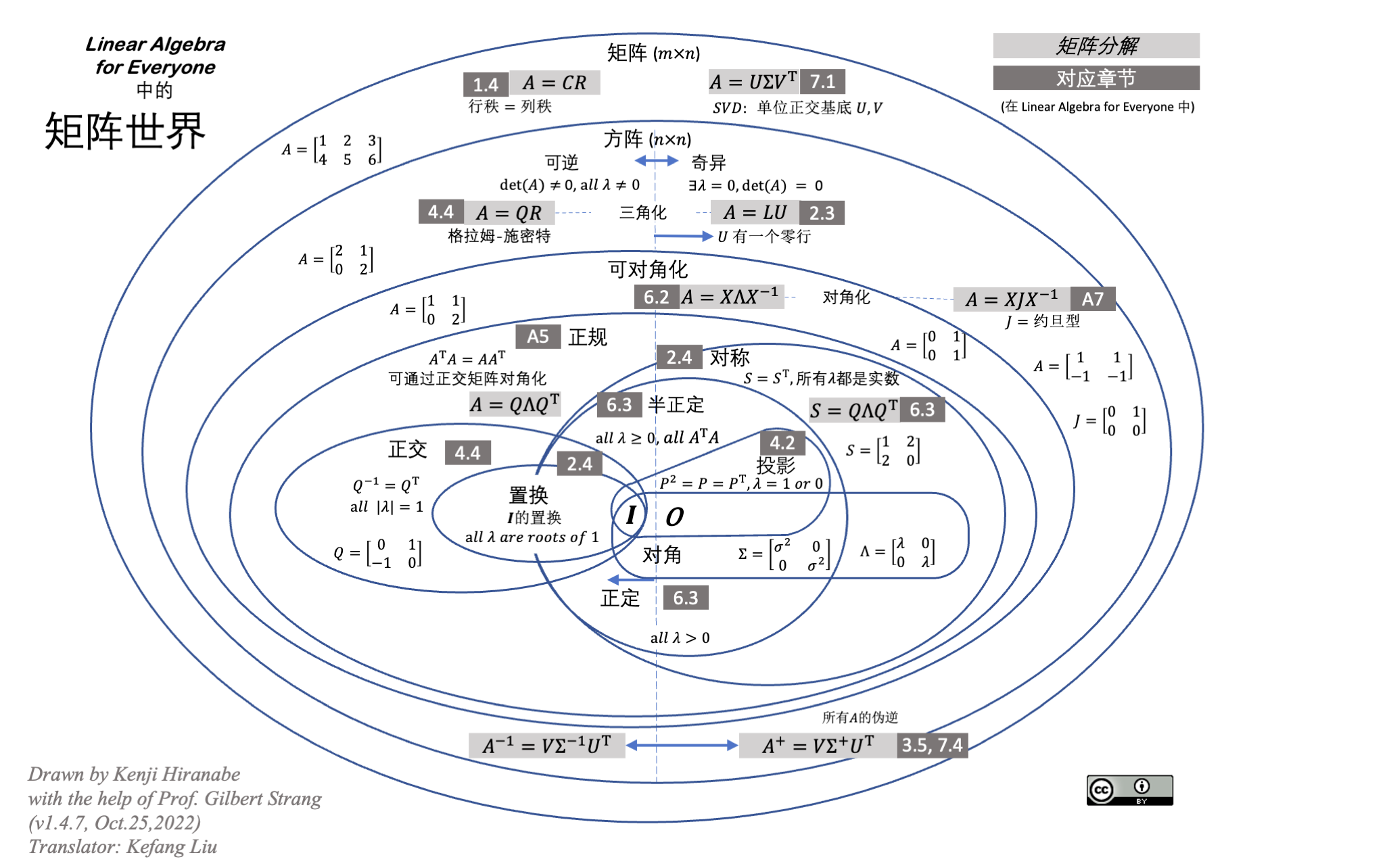
kenjihiranabe——The-Art-of-Linear-Algebra-zh-CN
详细计算方法与理论:见矩阵论
线性代数的本质在于将具体事物抽象为数学对象,并描述其静态和动态特性
最基本的概念是 set
集合的定义是由某些具有某些共性的对象汇总成的集体。
将这些对象用数字或符号表示(对象映射到数域),这样集合中的元素就变为了多个数字或符号以某种方式排列成的组合