计算机中数的表示与运算
ALU构造
1.1 字符和字符串
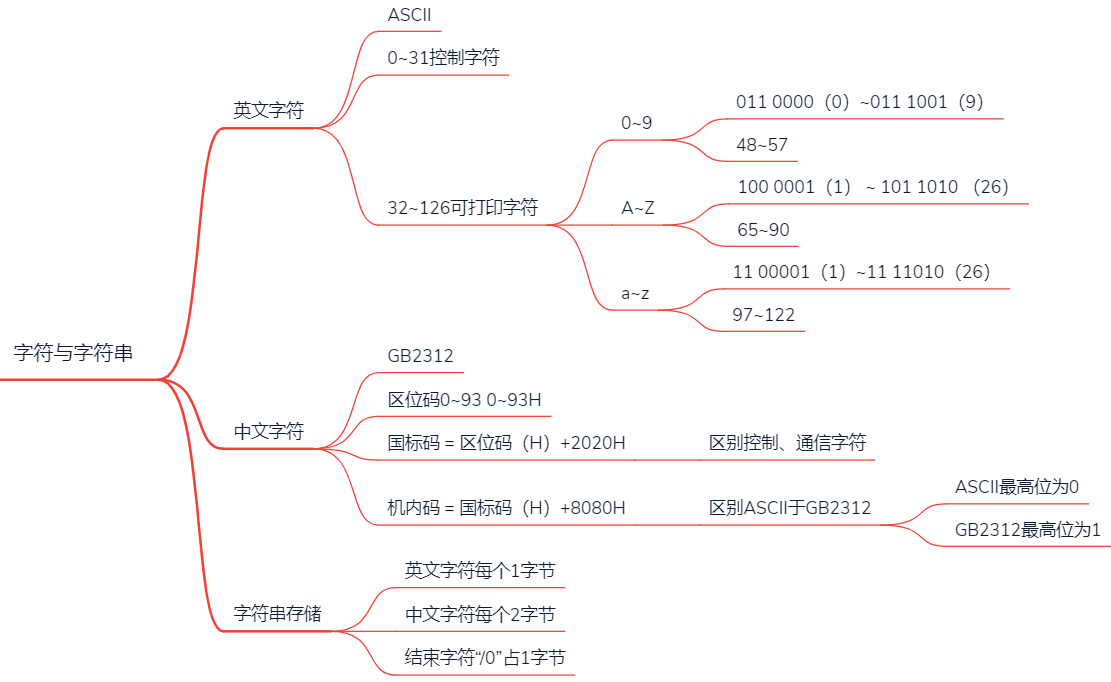
1.2 数据存储与排列
1.2.1 存储模式
多字节数据在内存中一定占连续的字节
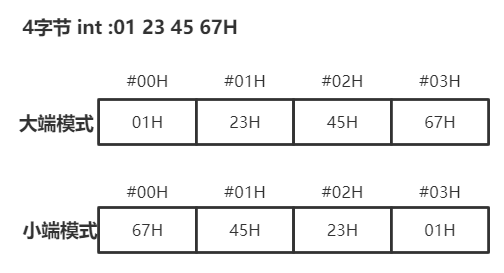
大端模式:高字节(MSB)低地址
小端模式:低地址(LSB)低字节
一个多字节数据,必须存放在连续的地址单元
1.2.2 边界对齐
这里的字:指计算机一次可同时处理的二进制位数,即
机器字长
边界对齐:访问一个字/半字只需一次访存
边界不对齐:访问一个字/半字可能需要两次访存
若假设机器字长为4字节,分别采用边界对齐方式和边界不对齐方式存储三个数据
分别为3字节,两个半字,一个字
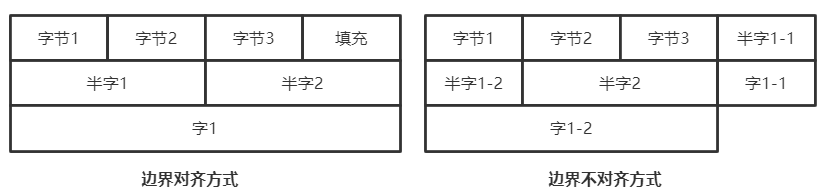
边界对齐方式,每个数据从新字开始,(低2位地址线引脚接地)
- 边界不对齐方式,每个数据从上个数据结尾开始
1.3 二进制
1.3.1 计算机采用二进制原因
- 可行性:二进制只有01两个状态,能标识01两种状态的电子器件很多。
- 运算简易性:二进制运算法则少,运算简单,简化硬件结构
- 有逻辑代数的理论基础:二进制0和1正好和逻辑代数的真假对应
1.3.2 编码(二进制的解释方式)
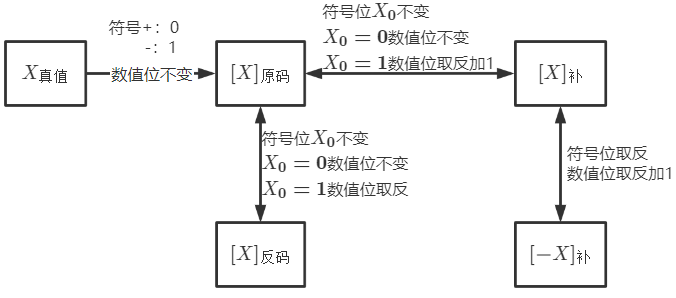
原码
n+1位定点整数 $1\underbrace{1\cdots11}_{n}.\sim 0\underbrace{11\cdots1}_n.$ :范围 $-2^n-1\sim2^n-1$
n+1位定点小数 $1.\underbrace{11\cdots 11}_{n}\sim 0.\underbrace{11\cdots 11}_n$ 范围 $-1+2^{-n}\sim 1-2^{-n}$
- 字长足够,则可表示任意整数
- 不能表示任意小数,只能是2的整数次幂
- 真值0不唯一,可表示数少1
反码
真值0不唯一:+0,-0
表示数值的范围和原码相同
补码
$n+1$ 位二进制数可表示
- 定点整数 $1,\underbrace{00\cdots 00}_n.\sim 0,\underbrace{11\cdots 11}.$ :$-2^n \sim 2^n-1$
- 定点小数 $1.\underbrace{00\cdots00}_n\sim 0.\underbrace{11\cdots11}_n$ : $-1\sim 1-2^{-n}$
补码特点(机内码)
- 真值0的补码唯一
- 正数的补码二进制表示的无符号数,小于负数的补码表示的无符号二进制数
- 如:127:0111 1111,-1;
- 数值位1越多表示数字越大
- 0同侧编码值越大,真值越大
- 正数的2进制编码小于负数的二进制编码 1000(-8) <0111(7)
原码变为补码:从右到左,找到第一个1,其左边取反,其右边不变
- 正数补码等于原码(什么编码都不变)
- 负数补码等于原码取反加一
编码方式与范围
n位2进制编码
| 编码方式 | 最小值编码 | 最小值 | 最大值编码 | 最大值 | 数值范围 |
|---|---|---|---|---|---|
| 无符号定点整数 | $\underbrace{00…00}_n.$ | 0 | $\underbrace{11…11}_n.$ | $2^{n+1}-1$ | $0\le x\le 2^{n+1}-1$ |
| 无符号定点小数 | $.\underbrace{00…00}_n$ | 0 | $0.\underbrace{11…11}_n$ | $1-2^{-n}$ | $0\le x\le 1-2^{-n}$ |
| 原码定点整数 | $1,\underbrace{1…11}_{n-1}.$ | $-2^n+1$ | $0,\underbrace{1\cdots11}_{n-1}.$ | $2^n-1$ | $-2^n+1\le x \le 2^n-1$ |
| 原码定点小数 | $1.\underbrace{1…11}_{n-1}$ | $-1+2^{-n}$ | $0.\underbrace{1…11}_{n-1}$ | $1-2^{-n}$ | $-1-2^{-n}\le x \le 1-2^{-n}$ |
| 补码定点整数 | $1,\underbrace{0…00}_{n-1}.$ | $-2^n$ | $0,\underbrace{1…11}_{n-1}.$ | $2^n-1$ | $-2^n\le x \le 2^n-1$ |
| 补码定点小数 | $1.\underbrace{0…00}_{n-1}$ | $-1$ | $0.\underbrace{1…11}_{n-1}$ | $1-2^{-n}$ | $-1\le x \le 1-2^{-n}$ |
移码
真值加一个常数
- 只能表示整数
- 真值0唯一
- 移码大小与数值的大小一致
- 移码大,真值大
- 移码小,真值小
n位二进制能表示 $2^n$ 个数字
1.3.3 无符号整数
用于表示内存地址信息
表示范围 $0\sim 2^n-1$
若寄存器位数小于无符号定点整数,舍去高位 发生上溢出
1.3.4 定点数运算
移位
逻辑移位
无符号数,空位填0
算术移位
有符号数
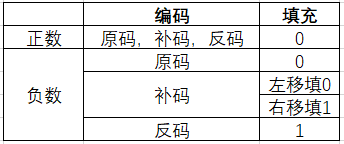
循环移位
丢弃位会存在 CF 中
适用情况:高低字节数据互换
加法
原码
符号位相同:绝对值相加,符号位不变
符号位不同:符号等于绝对值大者
机内实现两种策略
- 转换为补码后,用补码加减法实现,结果再转回原码
- 直接用原码进行加减,符号与数值分开运算
补码
符号位和尾数一起运算
补码运算结果为补码
补码加减运算:
- 当参加运算的数是定点小数时,模 $M=2$
- 当参加运算的数是定点整数时,模 $M=2^{n+1}$
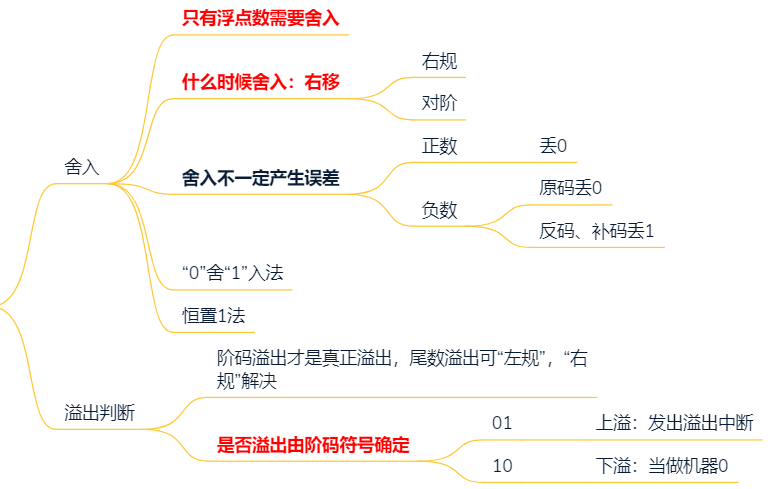
溢出判断
只有 “正数+正数” 才可能 上溢 —— 正+正=负
只有 “负数+负数” 才可能 下溢 —— 负+负=正
采用一位符号位 (模2补码)
设 A 的符号位为 $A_s$ ,B的符号位为 $B_s$ ,运算结果符号位为 $S_s$ ,则溢出表达式为 $V=\underbrace{A_sB_s\overline{S_s}}_{001}+\underbrace{\overline{A_s}\overline{B_s}S_s}_{110}$
- $V=1$ ,表示无溢出
- $V=0$ ,表示有溢出
如:
根据进位情况判断
| 符号位进位 $C_S$ | 最高数值位进位 $C_1$ | |
|---|---|---|
| 上溢 | 0 | 1 |
| 下溢 | 1 | 0 |
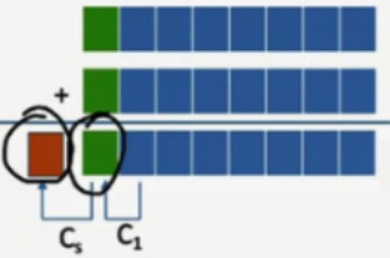
即:$C_s$ 与 $C_1$ 不同时有溢出
溢出判断表达式为 $V=C_s\oplus C_1$
- $V=0$ ,表示无溢出
- $V=1$ ,表示有溢出
双符号位 (模4补码)
正数符号00,负数符号11
记两个符号位为 $S_{s1}S_{s2}$ ,则 $V=S_{s_1}\oplus S_{s_2}$
- $V=0$ ,表示无溢出
- $V=1$ ,表示有溢出
上溢:超出表示范围的上边界
下溢:低于表示范围的下边界
注意:
- 实际存储时只存一位符号位,在运算时复制
- 双符号位,算术移位只有低位符号位参与(由于实际只存1位)
乘法
原码一位乘
结果的符号位通过 异或 确定
- 符号位不参与运算,可以省略
- 原码一位乘可以只用单符号位
数值部分通过被乘数和乘数绝对值的n轮 加法、移位 完成
根据当前乘数中参与运算的位确定 (ACC) 加什么
- 为0,则 $(ACC)+0$
- 为1,则 $(ACC)+[\mid x\mid]_原$
每轮加法后,ACC,MQ的内容统一 逻辑右移
如
设机器字长5位(1位符号位,4位数值位),$x=(13)_{10}=+1101,y=(-11)_{10}=-1011$ ,采用原码一位乘法求 $x\times y$
符号位 $P_s = x_s\oplus y_s=0\oplus 1=1$
$\mid x\mid = 1101,\mid y\mid = 1011$ ,原码一位乘法的求解过程如下
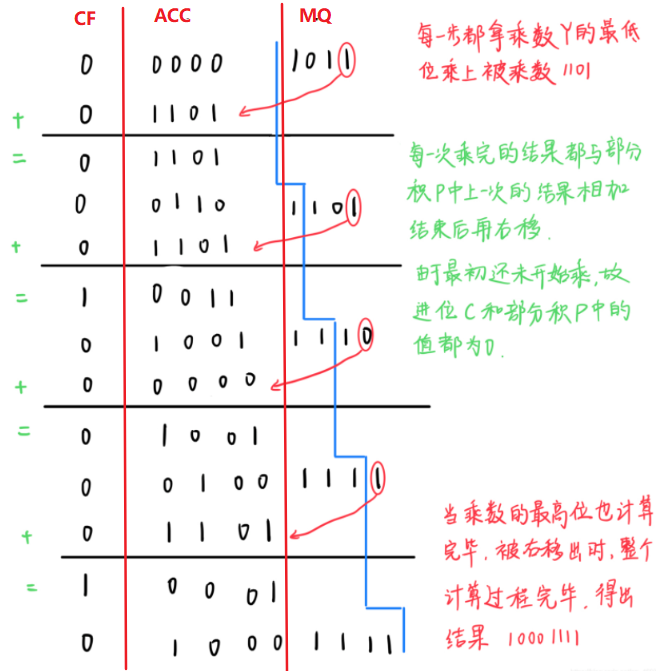
最后结果为 $P_s+(ACC)+(MQ)=1.1000\quad1111=-0.1000\quad1111$
还不懂的话去看:https://blog.csdn.net/qq_46077337/article/details/112401439
补码一位乘(Booth法)
增加一位辅助位,补充到最低位,初始值为 $0$
n轮加法,加法规则

补码的算数右移,符号位不动,数值位右移
符号位是什么就补什么
如
设机器字长5位(1位符号位,4位数值位),$x=(-13)_{10}=-0,1101,y=(11)_{10}=+0,1011$ ,采用补码一位乘法求 $x\times y$
$[x]_补=11,0011,[-x]_{补}=00,1101$
计算过程

- 结果:$[x·y]_{补}=11.0111\quad 0001$,即 $x·y=-0.1000\quad 1111$
还不懂的话去看:https://zhuanlan.zhihu.com/p/367308695
除法

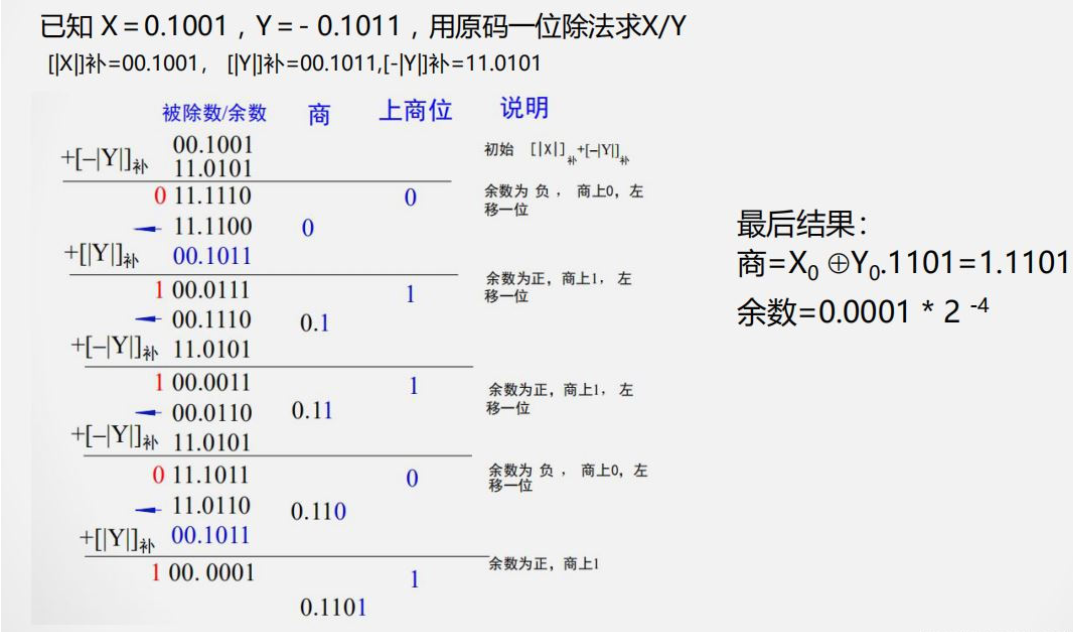
原码一位除
符号位 $Q_s = x_s\oplus y_s$
恢复余数法:当余数为负时,上商0,并 $+除数$ ,再左移,再 $-除数$
加减交替法:当余数为负时,上商0,并左移,再 $+除数$

补码一位除
- 符号位参与运算,除数和被除数均用双符号位表示
被除数与除数同号,被除数减去除数;
被除数与除数异号,被除数加上除数
余数和除数同号,商为1,余数左移一位,下次减除数;
余数和除数异号,商为0,余数左移一位,下次加除数。
重复步骤2,包括符号在内,工作n+1步
如
已知 x=0,1011,y=0,1101,用补码加减交替法求 $\frac{x}{y}$
$[x]_补=00,1011,[y]=00,1101,[-y]_补=11,0011,n=4$
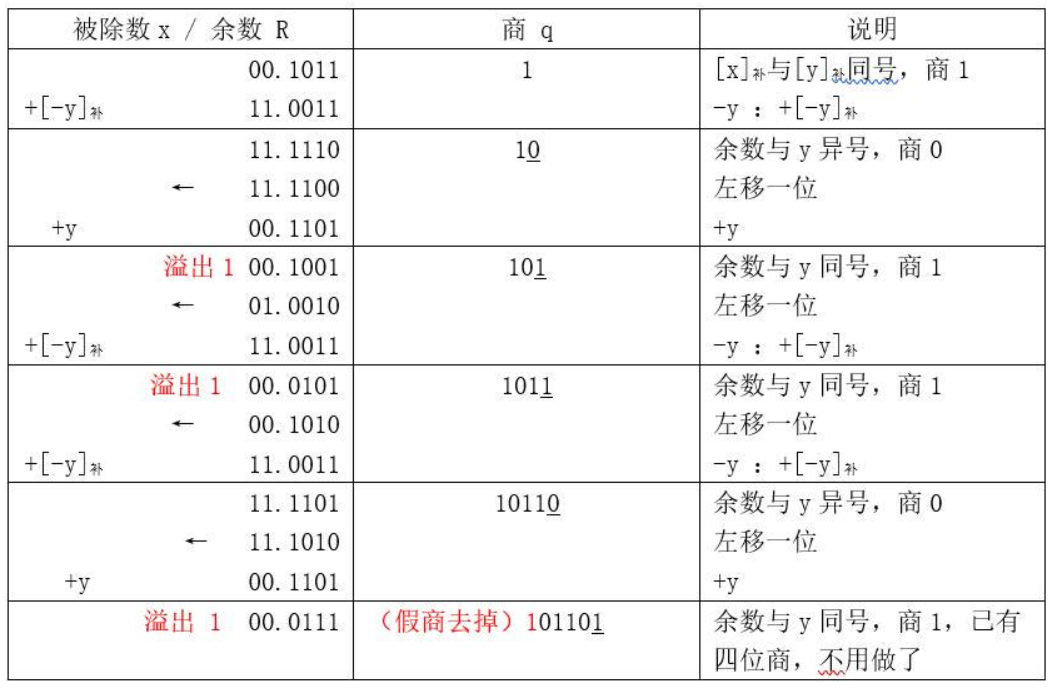
商 $[Q]_补=0,1101$,余数 $[R]_补=0,0111$
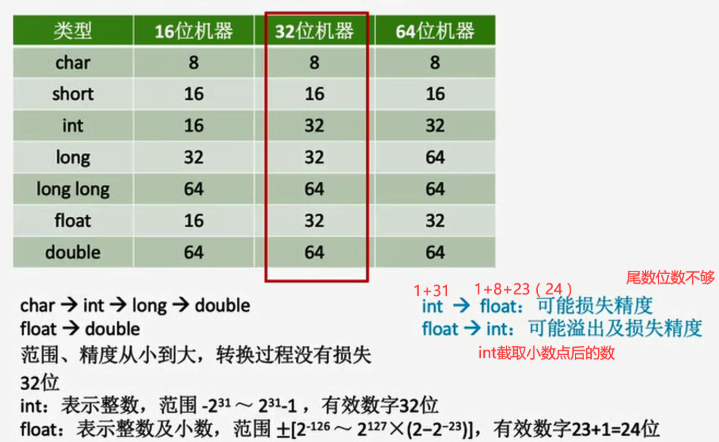
强制类型转换
等字长无符号数与有符号数
位值不变,改变解释方式
不同字长整数之间转换
大字长到小字长
将多余高位字长部分截断,低位赋值
小字长到大字长
数值相等,高位进行符号位填充
填充规则
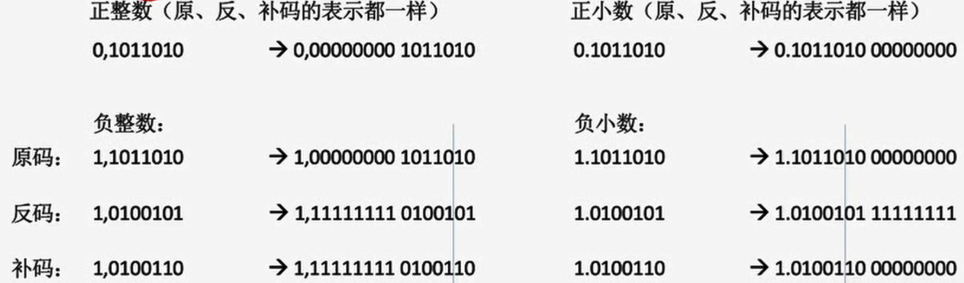
定点整数:在原符号位和数值位中间添加新位
正数加0
负数:原码加0;反,补码加1
定点小数:在原数值位后面添加新位
正数都加0
负数:原、补码加0,反码加1
1.3.5 浮点数运算
引入目的
- 在二进制位数不变的前提下,扩展可表示范围
- 定点数精度比浮点数大
格式
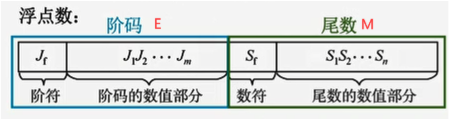
浮点数数值: $N=r^E\times M$
阶码
阶码反映浮点数表示范围及小数点位置
阶码是用补码或移码表示的定点整数
阶码的表示算数左移位数
尾数
尾数反映精度
尾数是用原码或补码表示的定点小数
尾数越少,可表示的精度越低
如
7位阶码,1位数符,8位尾数。若阶码用移码,尾数用补码表示,则浮点数所能表示数的范围
阶码最大 $2^7-1=63$
尾数范围 $-1\sim 1-2^{-8}$
$-2^{63}\sim (1-2^{-8})\times2^{63}$
规格化
没有隐含1,尾数最小值为-1
有隐含1,尾数最小值 $-(2-2^n)$
尾数规格化
规格化浮点数:规定位数的最高数值位必须是一个有效值
左规:当浮点数运算的结果为非规格化时要进行规格化处理,将 尾数算数左移一位,阶码减一
右规:当浮点数运算的结果位数出现溢出(双符号位为01或10)时,将 尾数算数右移一位,阶码加一

用原码表示的尾数进行规格化
正数 $0.1XXX..XX$ 的形式。其最大值表示为 $0.\underbrace{11..1}_{n}$ ,最小值表示为 $0.10..0$ 。尾数的表示范围为 $\frac{1}{2}\le M\le (1-2^{-n})$
负数为 $1.1XXX..XX$ 的形式。 其最大值表示为 $1.\underbrace{10..0}_n$ ,最小值表示为 $1.\underbrace{11..1}_n$ 。尾数的表示范围为 $-(1-2^{-n})\le M\le-\frac{1}{2}$
用补码表示的尾数进行规格化
正数 $0.1XX..X$ 的形式。其最大值表示为 $0.\underbrace{11…1}_n$ ,最小值表示为 $0.10..0$。尾数的表示范围为 $\frac{1}{2}\le M\le (1-2^{-n})$ 。
负数 $1.0XX..X$ 的形式。其最大值表示为 $1.\underbrace{01…1}_n$ ,最小值表示为 $1.00..0$ 。尾数的表示范围为 $-1\le M\le -(\frac{1}{2}+2^{-n})$
浮点数可表示范围
阶码和尾数均用补码 表示,阶码部分共 $K+1$ 为(含1位阶符),尾数部分共 $n+1$ 位(含1位数符),则这样的浮点数的表示范围是多少
| 浮点数 | 阶码 | 尾数 | 真值 |
|---|---|---|---|
| (规格化)最大正数 | $0,\underbrace{1\cdots 1}_K$ | $0.\underbrace{11\cdots 11}_n$ | $(1-2^{-n})\times 2^{2^k-1}$ |
| 最小正数 | $1,\underbrace{0\cdots 0}_K$ | $0.\underbrace{00\cdots 01}_n$ | $2^{-n} \times 2^{2^{-k}}$ |
| 规格化最小正数 | $1,\underbrace{0\cdots 0}_K$ | $0,\underbrace{10\cdots 0}_n$ | $2^{-1}\times 2^{-2^{k}}$ |
| (规格化)最小负数 | $0,\underbrace{1\cdots 1}_k$ | $1.\underbrace{00\cdots 00}_n$ | $(-1)\times 2^{2^k-1}$ |
| 最大负数 | $1,\underbrace{0\cdots 0}_K$ | $1.\underbrace{11\cdots 11}_n$ | $-2^{-n}\times 2^{-2^k}$ |
| 规格化最大负数 | $1,\underbrace{0\cdots 0}_K$ | $1.\underbrace{01\cdots 11}_n$ | $-(2^{-n}+2^{-1})\times 2^{-2^k}$ |
IEEE754
引入目的:增加数据的表示精度
格式
规格化的单精度浮点数:$(-1)^s\times 1.M\times 2^{E-127}$
IEEE754浮点数表示与符号位表示类似,将各部分分别表示后,添加符号位
- 尾数实际位数为24bit——隐含1
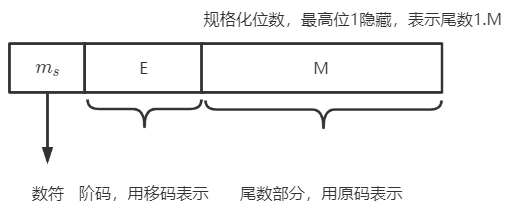
| 类型 | 数符s位数 | 阶码E位数 | 尾数M位数 | 总位数 | 阶码偏移值$(2^{阶码位数}-1)$ |
|---|---|---|---|---|---|
| 单精度浮点数(float) | 1 | 8$(-126\sim 127)$ | 23 | 32 | 127 |
| 双精度浮点数(double) | 1 | 11 | 52 | 64 | 1023 |
IEEE754阶码
$E-127=E的二进制表示+1000 0001$
阶码真值=阶码无符号整数值-阶码偏移值
| 阶码 | 无符号整数 | 阶码真值(IEEE偏移值$-(2^{n-1}-1)$) |
|---|---|---|
| 0000 0001 | 1 | -126 |
| 0000 0010 | 2 | -125 |
| … | … | … |
| 0111 1111 | 127 | 0 |
| 1000 0000 | 128 | 1 |
| … | … | … |
| 1111 1110 | 254 | 127 |
阶码全0和全1代表特殊含义
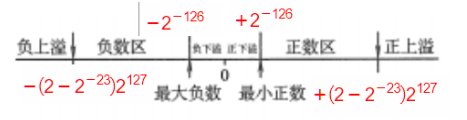
IEEE754浮点数范围
| 格式 | 规格化的最小绝对值 | 规格化的最大绝对值 |
|---|---|---|
| 单精度 | E=1;M=0;$1.0\times 2^{1-127}=1.0\times 2^{-126}$ | E=254;M=.11…1;$1.11…1\times 2^{254-127}=(2-2^{-23})\times 2^{127}$ |
| 双精度 | E=1;M=0;$1.0\times 2^{1-1023}=1.0\times 2^{-1022}$ | E=2046;M=.11…1;$1.11…1\times 2^{2046-1023}=(2-2^{1023})\times 2^{1023}$ |
阶码E全为0,尾数不是非规格化小数
- 尾数M不全为0——非规格化小数
- 尾数M全为0——真值0
阶码E全为1,尾数M全为0——无穷大
阶码E全为1,尾数M不全为0——非数值
溢出
加减运算

强制类型转换
- IEEE754尾数默认省略最高位1
- 当
int类型转浮点数类型,若整数位数>24位,会有舍入误差
举例
若
i是一个int型整数,f和d分别为float型(32位) 和double(64位) 实数。判断各布尔表达式的布尔值
i==(int)((double)i)true: int 32位有效数字,double为52+1=53位有效数字,所以强制转化为 double 类型后在转回去不会 发生精度损失f == (float)((int)f)false: float 型有小数部分,转为int后可能没有小数部分float转为int有32位有效数字,再转回float后,可能丢失有效数字
f == (float)((double)f)true: double比float精度高,float转为double不会丢失精度d == (double)((float)f)false: float尾数有效位数小于double,所以(float)f会丢失精度,再转回 double后,不相等

1.4 运算器构造与功能


1.5 加法器
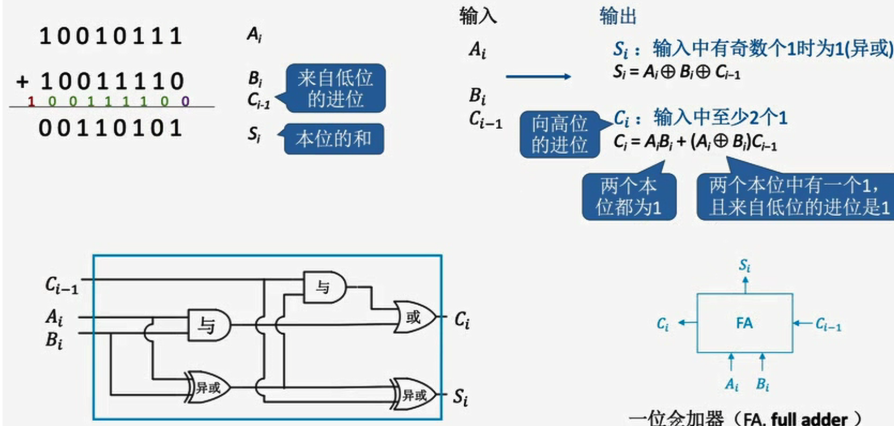
1.5.1 一位全加器FA
作用:求本位和、进位
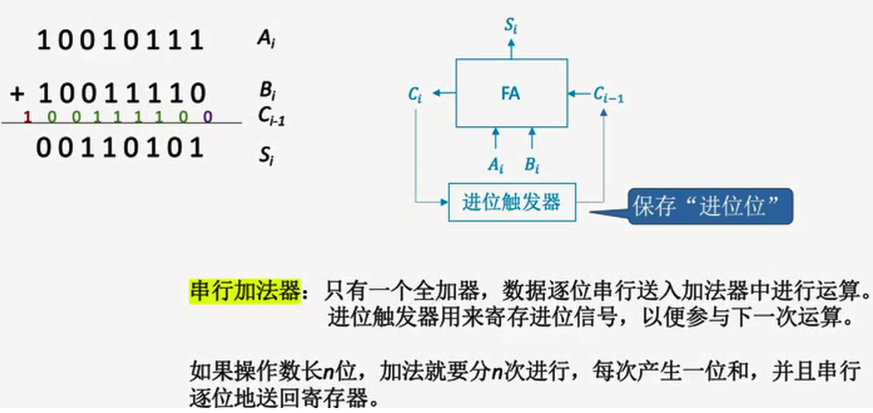
1.5.2 串行加法器
作用:完成两个n位二进制数的加法
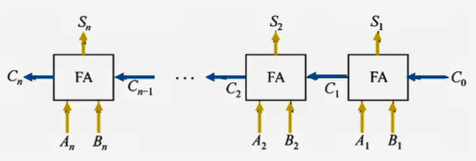
1.5.3 并行加法器
根据进位计算公式,发现当前公式中进位是上一公式计算得出的,而上一公式中的进位是由其上一位公式计算的出的。最终可以展开到 $C_0$ ,这样 $C_i$ 就不需要等待 $C_{i-1}$ 计算完成后再进行计算。
串行连接
将n个并行全加器串接起来,就可进行两个n位数相加
串行进位又称行波进位,每一级的进位直接依赖于前一级的进位,即进位信号是逐级形成的
- 运算的速度取决于进位产生和传递速度
并行连接
并行进位的并行加法器(先行进位,同时进位):各级进位信号同时生成
- $G_i$ 为进位产生函数,当 $G_i==1$ 时,一定会产生进位
- 进位传递函数:当 $A_i$ 与 $B_i$ 只有一个1,会把 $C_{i-1}$ 传递到高位 $C_i$
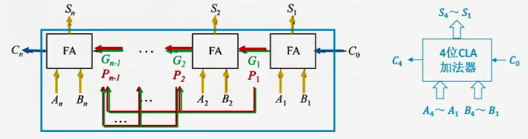
根据进位函数,构造 先行进位电路CLA
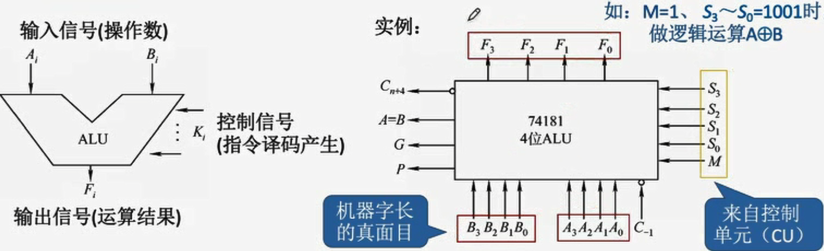
ALU
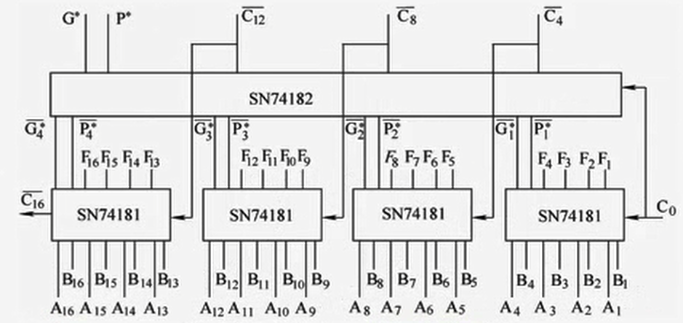
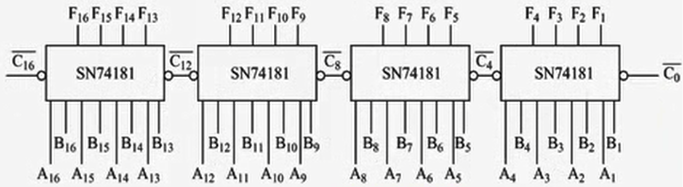
1.5.4 分组并行进位加法器
单级先行进位
组内并行、组件串行
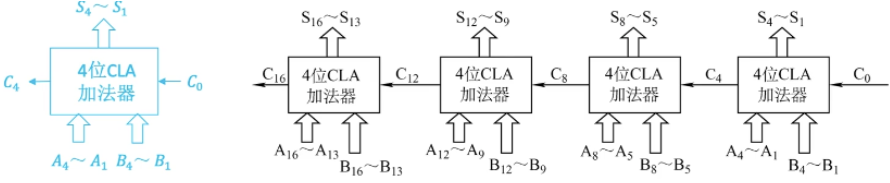
由于并行加法器在计算进位时,越高位用到的逻辑门元件越多,而 $C_1\sim C_4$ 的产生速度很快, 所以将一个4位CLA作为一个组,组内进位可同时得出,产生一个组进位
只有得到前一组的进位信号,本组才可以计算
ALU
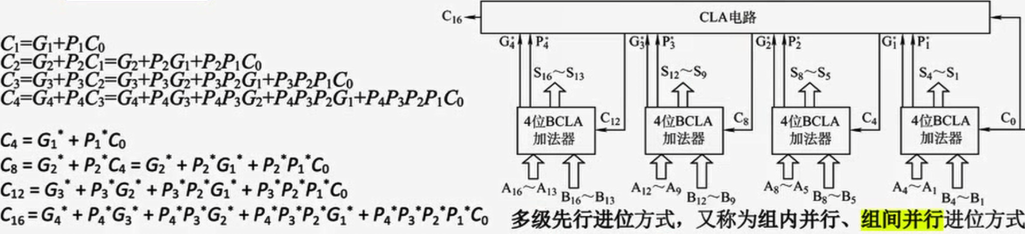
多级先行进位
组内并行,组件并行
多个组的进位信号同时产生
ALU