2.矩阵分解——奇异值与奇异值分解

矩阵分解可以得到简化的乘积矩阵，可以简化后续的计算与处理度

2.1 奇异值与SVD

2.1.1 奇异值

给定 $A=A_{n\times p}$ ，则 $A^HA$ 与 $AA^H$ 有相同的正根 $\lambda_1\ge \lambda_2\ge \cdots\ge\lambda_r\ge0$ ，称 $\sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_r}$ 为 $A$ 的奇异值

若 $r(A^HA)=r(AA^H)=r(A)=r$ ，恰有 $r$ 个正根 $\lambda_1\ge\lambda_2\ge\cdots\ge \lambda_r > 0$ ，则称 $\sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_r}$ 为 $A$ 的正奇异值，记作 $S_+(A)=\{s_1,s_2,\cdots,s_r\}=\{\sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_r}\}$ ，且 $\sqrt{\lambda_1}$ 称为最大奇异值

对于 $n$ 阶方阵 $A=A_{n\times n}$ ，则 $A^HA$ 与 $AA^H$ 有 $n$ 个相同非负根，则 $\lambda_1\ge\cdots\ge \lambda_n\ge 0$，此时 $\sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_n}$ 为 $A$ 的全体奇异值，记作 $S(A)=\{s_1,s_2,\cdots,s_n\}={\sqrt{\lambda_1},\sqrt{\lambda_2},\cdots,\sqrt{\lambda_n}},\lambda_1\ge \cdots\ge \lambda_r,\lambda_{r+1}=\cdots=\lambda_n=0$

a. 正奇值例题

$\begin{aligned} &(1)A=\left( \begin{matrix} 1&2\\ 0&0\\ 0&0 \end{matrix} \right)\quad (2)A=\left( \begin{matrix} 1&1\\ 0&0\\ 1&1 \end{matrix} \right) \quad (3)A=\left( \begin{matrix} 1&-1\\ 1&1 \end{matrix} \right) \\\\ &(1)A^HA=\left( \begin{matrix} 1&2\\ 2&4 \end{matrix} \right),为秩1矩阵，可知\lambda(A^HA)=\{5,0\}\\ &\therefore s^+(A)=\{\sqrt{5}\}\\\\ &(2)A^HA=\left( \begin{matrix} 2&2\\ 2&2 \end{matrix} \right)，为秩1矩阵，则\lambda(A)=\{4,0\}\\ &则s^+(A)=\{2\}\\\\ &(3)A^HA=\left( \begin{matrix} 2&0\\ 0&2 \end{matrix} \right),为对角阵，\therefore\lambda(A^HA)=\{2,2\}\\ &则 s^+(A)=\{\sqrt{2},\sqrt{2}\} \end{aligned}$

b. 半正定Hermite阵的奇异值与特征值相同

$\begin{aligned} &设全体特征值为 \lambda(A)=\{\lambda_1,\cdots,\lambda_n\}，且A^H=A\Rightarrow A^HA=A^2,\\ &\therefore 可知\lambda(A^HA)=\lambda(A^2)=\{\lambda_1^2,\cdots,\lambda_n^2\}\\ &\because A半正定可知\lambda_1\ge 0,\cdots,\lambda_n\ge 0\\ &故，全体奇异值s(A)=\{\sqrt{\lambda_1^2},\cdots,\sqrt{\lambda_n^2}\}=\{\lambda_1,\cdots,\lambda_n\}=\lambda(A) \end{aligned}$

2.1.2 奇异值分解SVD

a. 正SVD

设 $A=A_{m\times n}$ ，$r(A)>0$ ,正奇值 $\sqrt{\lambda_1},\cdots,\sqrt{\lambda_r}$，则有分解 $A=P\Delta Q^H$ ，其中 $\Delta=\left(\begin{matrix}\sqrt{\lambda_1}&&\\&\ddots&\\&&\sqrt{\lambda_r}\end{matrix}\right)$，$P_{m\times r}$ ，$Q_{n\times r}$ 为半U阵，$P^HP=I_r=Q^HQ$ ，可写正SVD公式 $A=P\left(\begin{matrix}\sqrt{\lambda_1}&&\\&\ddots&\\&&\sqrt{\lambda_r}\end{matrix}\right)Q^H$

证明：

$P_{m\times r}，Q_{n\times r}$ 的构造
$A^HA$ 为Hermite阵，由Hermite分解定理，存在U阵，使 $U^H(A^HA)U=\left( \begin{matrix}\lambda_1&&\\&\ddots&\\ &&\lambda_n \end{matrix} \right)_{n\times n}$ ，且 $A^HA$ 为半正定阵，有 $\lambda_1,\cdots,\lambda_r>0，\lambda_{r+1}=\cdots=\lambda_n=0,r(A)=r$
。而 $U$ 的列向量 $(q_1,q_2,\cdots,q_n)$ 为 $A^HA$ 的特征向量
且 $A^HAq_1=\lambda_1q_1,\cdots,A^HAq_r=\lambda_rq_r,A^HAq_{r+1}=0,A^HAq_{n}=0$ ，令 $Q=(q_1,q_2,\cdots,q_r)_{n\times r}$ ，$P=(\frac{Aq_1}{\vert Aq_1\vert},\cdots,\frac{Aq_r}{\vert Aq_r\vert})_{m\times r}$
P与Q为半U阵
已知 $Q$ 中列向量为U阵的 $r$ 个非零列向量，则 $Q$ 为半U阵，而 $(Aq_1,Aq_2)=(Aq_2)^H(Aq_1)=q_2A^HAq_1=\lambda_1q_2^Hq_1=(\lambda_1q_1,q_2)=0$ 。同理， $Aq_i$ 与 $Aq_j$ 都正交，$\vert Aq_i\vert^2=(Aq_i)^H(Aq_i)=q_i^HA^HAq_i=\lambda_iq_i^Hq_i=\lambda_i\ge0$
$\Rightarrow P=\left(\frac{Aq_1}{\vert Aq_1 \vert},\frac{Aq_2}{\vert Aq_2 \vert},\cdots,\frac{Aq_r}{\vert Aq_r \vert}\right)=\left(\frac{Aq_1}{\sqrt{\lambda_1}},\frac{Aq_2}{\sqrt{\lambda_2}},\cdots,\frac{Aq_r}{\sqrt{\lambda_r}}\right)$，即 $P$ 阵为半U阵
代入$P,Q$
$P\Delta Q^H=\left(\frac{Aq_1}{\sqrt{\lambda_1}},\frac{Aq_2}{\sqrt{\lambda_2}},\cdots,\frac{Aq_r}{\sqrt{\lambda_r}}\right) \left( \begin{matrix}\sqrt{\lambda_1}&&\\ &&\ddots&\\ &&&\sqrt{\lambda_r} \end{matrix} \right)\left( \begin{matrix} q_1^H\\ q_2^H\\ \vdots\\ q_r^H \end{matrix} \right)$
$=(Aq_1,Aq_2,\cdots,Aq_r)\left( \begin{matrix} q_1^H\\ q_2^H\\ \vdots\\ q_r^H \end{matrix} \right)=\left(Aq_1q_1^H,Aq_2q_2^H,，\cdots,Aq_rq_r^H,\right)$
验证 $\left(Aq_1q_1^H,Aq_2q_2^H,，\cdots,Aq_rq_r^H\right)=A$
$A^HA$ 为半正定Hermite阵，$r(A^HA)=r(A)=r$。由同解定理，$A^HAx=0\iff Ax=0$ ，$A^HAq_{r+1}=\cdots=A^HAq_{n}=0\Rightarrow Aq_{r+1}=\cdots=Aq_{n}=0$
$\Rightarrow A(q_{r+1}q_{r+1}^H+\cdots+q_nq_n^H)=0$ ，而 $A(q_1q_1^H+\cdots+q_rq_r^H+q_{r+1}q_{r+1}^H+\cdots+q_nq_n^H)=AI=A$ ，即 $A(q_1q_1^H+\cdots+q_rq_r^H)=A$

最后得证正SVD公式，$A=P\Delta Q^H=P\left(\begin{matrix}\sqrt{\lambda_1}&&\\&\ddots&\\&&\sqrt{\lambda_r}\end{matrix}\right)Q^H$

分解方法

求 $A^HA$ 的特征值，$\lambda_1\ge\cdots,\ge\lambda_r>0$
正奇值为 $\sqrt{\lambda_1},\cdots\sqrt{\lambda_r}$
求 $\lambda_1,\cdots,\lambda_r$ 的正交特征向量（不必单位化）
令列半U阵 $Q=\left(\frac{X_1}{\vert X_1\vert},\cdots,\frac{X_r}{\vert X_r\vert}\right),P=\left(\frac{AX_1}{\vert AX_1\vert},\cdots,\frac{AX_r}{\vert AX_r\vert}\right)$

eg

$\begin{aligned} A=\left( \begin{matrix} 1&1\\ 0&0\\ 1&1 \end{matrix} \right) \end{aligned}$ $\begin{aligned} &A^HA=\left( \begin{matrix} 2&2\\ 2&2 \end{matrix} \right),由A^HA为秩1矩阵，得\lambda=\{4,0\}，正奇值为\sqrt{\lambda}=\sqrt{2}\\ &而\lambda_1=4的特征向量为X_1=\left( \begin{matrix} 1\\1 \end{matrix} \right),则\Delta=\left( 2 \right)\\ &令Q=\left(\frac{X_1}{\vert X_1\vert}\right)=\left( \begin{matrix} \frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}} \end{matrix} \right),P=\left( \begin{matrix} \frac{AX_1}{\vert AX_1\vert} \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{2}}\\0\\\frac{1}{\sqrt{2}} \end{matrix} \right)\\ &则A的正SVD为A=P\Delta Q^H=\left( \begin{matrix} \frac{1}{\sqrt{2}}\\0\\\frac{1}{\sqrt{2}} \end{matrix} \right)\left(2\right)\left( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right) \end{aligned}$

考虑 $B=\left(\begin{matrix}1&0&1\\1&0&1\\\end{matrix}\right)$ 的正SVD

$\begin{aligned} &已知B=A^H,且有A的正SVD，A=P\Delta Q^H=\left( \begin{matrix} \frac{1}{\sqrt{2}}\\0\\\frac{1}{\sqrt{2}} \end{matrix} \right)\left(2\right)\left( \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \right)\\ &B=(P\Delta Q^H)^H=Q\Delta P^H=\left( \begin{matrix} \frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}} \end{matrix} \right)\left(2\right)\left( \frac{1}{\sqrt{2}},0,\frac{1}{\sqrt{2}} \right) \end{aligned}$

b. SVD(将P，Q，D都扩充为方阵)

$\begin{aligned} &设A=A_{m\times n}，r(A)>0,正奇值\sqrt{\lambda_1},\cdots,\sqrt{\lambda_r}>0,则有分解A=W\Delta V^H\\ &其中D=\left( \begin{matrix} \Delta&0\\ 0&0 \end{matrix} \right)_{m\times n}，W_{m\times m}=(P,P_1),V_{n\times n}=(Q,Q_1)\\ &可写SVD公式A=W\left( \begin{matrix} \Delta&0\\ 0&0 \end{matrix} \right)V^H=P\Delta Q^H,其中\left( \begin{matrix} \sqrt{\lambda_1}&&\\ &\ddots&\\ &&\sqrt{\lambda_r} \end{matrix} \right) \end{aligned}$

证明:

$\begin{aligned} &由正SVD：A=P\Delta Q^H,分别把P，Q扩充为U阵，即W=(P,P_1),V=(Q,Q_1)，\\ &V^H=\left( \begin{matrix} Q^H\\ A_1^H \end{matrix} \right),则WDV^H=(P,P_1)\left( \begin{matrix} \Delta&0\\ 0&0 \end{matrix} \right)\left( \begin{matrix} Q^H\\ A_1^H \end{matrix} \right)=\left( P\Delta\quad 0\\ \right)\left( \begin{matrix} Q^H\\ A_1^H \end{matrix} \right)=P\Delta Q^H \end{aligned}$

分解方法

求 $A^HA$ 的特征值，$\lambda_1\ge\cdots,\ge\lambda_r>0$
正奇值为 $\sqrt{\lambda_1},\cdots\sqrt{\lambda_r}$
求 $\lambda_1,\cdots,\lambda_r$ 的正交特征向量（不必单位化）
令列U半阵 $Q=\left(\frac{X_1}{\vert X_1\vert},\cdots,\frac{X_r}{\vert X_r\vert}\right),P=\left(\frac{AX_1}{\vert AX_1\vert},\cdots,\frac{AX_r}{\vert AX_r\vert}\right)$ ，则有正SVD：$A=P\Delta Q^H$
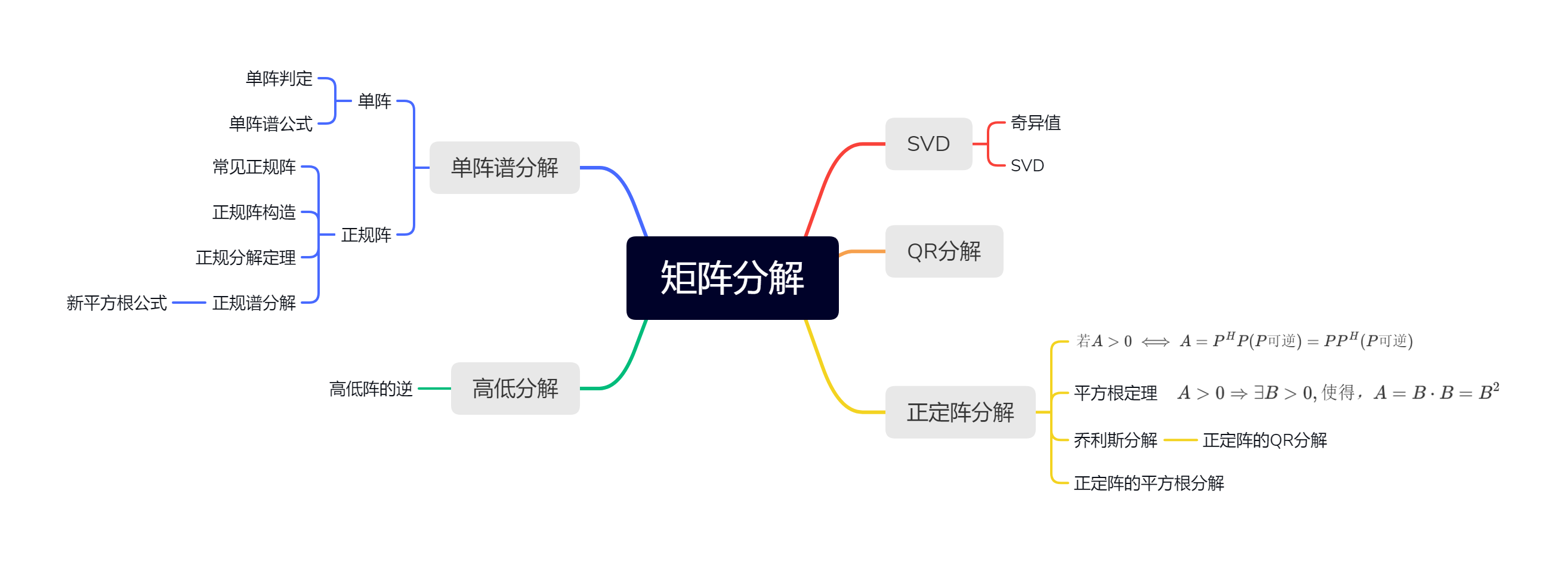
将P，Q扩充为W，V 扩充方法不唯一 由证明可知，不管 $P_1,Q_1$ 为何，都会被消去
得SVD公式 $A=WDV^H$

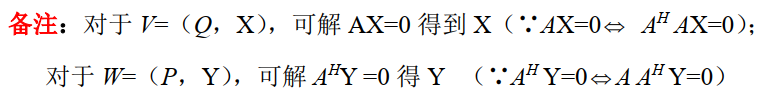
eg

$\begin{aligned} A=\left( \begin{matrix} 1&1\\ 0&0\\ 1&1 \end{matrix} \right) \end{aligned}$ $\begin{aligned} &扩充为两个U阵V=\left(Q,X\right)=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{matrix} \right),W=\left(P,Y\right)=\left( \begin{matrix} \frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\ 0&0&0\\ \frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}} \end{matrix} \right)\\ &则有奇异分解SVD，A=\left( \begin{matrix} \frac{1}{\sqrt{2}}&0&\frac{1}{\sqrt{2}}\\ 0&0&0\\ \frac{1}{\sqrt{2}}&0&-\frac{1}{\sqrt{2}} \end{matrix} \right)\left( \begin{matrix} 2&0\\ 0&0\\ 0&0 \end{matrix} \right)\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}} \end{matrix} \right) \end{aligned}$

$\begin{aligned} A=\left( \begin{matrix} 2i&1\\ 1&i\\ 1&i \end{matrix} \right) \end{aligned}$ $\begin{aligned} &A^HA=\left( \begin{matrix} -2i&1&1\\ 1&-i&-i \end{matrix} \right)\left( \begin{matrix} 2i&1\\ 1&i\\ 1&i \end{matrix} \right)=\left( \begin{matrix} 6&0\\ 0&3 \end{matrix} \right)，可知正奇值S(A)_+=\{\sqrt{6},\sqrt{3}\}\\ &\lambda_1=6,X_1=\left( \begin{matrix} 1\\0 \end{matrix} \right),AX_1=\left( \begin{matrix} 2i\\1\\1 \end{matrix} \right)\vert AX_1\vert=\sqrt{6};\lambda_2=3,X_2=\left( \begin{matrix} 0\\1 \end{matrix} \right),AX_2=\left( \begin{matrix} 1\\i\\i \end{matrix} \right)\\ &令Q=\left( \begin{matrix} X_1,X_2 \end{matrix} \right)=\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right),P=\left( \begin{matrix} \frac{AX_1}{\vert AX_1\vert},\frac{AX_2}{\vert AX_2\vert} \end{matrix} \right)=\left( \begin{matrix} \frac{2i}{\sqrt{6}}&\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}} \end{matrix} \right)\\ &则有正SVD，A=P\Delta Q^H=\left( \begin{matrix} \frac{2i}{\sqrt{6}}&\frac{1}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}}\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}} \end{matrix} \right)\left( \begin{matrix} \sqrt{6}&\\ &\sqrt{3} \end{matrix} \right)\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)^H\\ &可知SVD，A=WDV=\left( \begin{matrix} \frac{2i}{\sqrt{6}}&\frac{1}{\sqrt{3}}&0\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}}&\frac{1}{\sqrt{2}}\\ \frac{1}{\sqrt{6}}&\frac{i}{\sqrt{3}}&-\frac{1}{\sqrt{2}} \end{matrix} \right)\left( \begin{matrix} \sqrt{6}&\\ &\sqrt{3} \end{matrix} \right)\left( \begin{matrix} 1&0\\0&1 \end{matrix} \right)^H \end{aligned}$

一个SVD解答

$\begin{aligned} A=\left( \begin{matrix} i&2\\ 1&i\\1&i \end{matrix} \right)，求正SVD与SVD \end{aligned}$ $\begin{aligned} &\because A^HA=\left( \begin{matrix} -i&1&1\\ 2&-i&-i \end{matrix} \right)\left( \begin{matrix} i&2\\ 1&i\\1&i \end{matrix} \right)=\left( \begin{matrix} 3&0\\ 0&6 \end{matrix} \right)为对角阵，令\lambda_1=3,\lambda_2=6\\ &A^HA有两个特向X_1=\left( \begin{matrix} 1\\0 \end{matrix} \right),X_2=\left( \begin{matrix} 0\\1 \end{matrix} \right)(互正交)，正奇值为 \sqrt{\lambda_1}=\sqrt{3},\sqrt{\lambda_2}=\sqrt{6}\\ &AX_1=\left( \begin{matrix} i\\1\\1 \end{matrix} \right),AX_2=\left( \begin{matrix} 2\\i\\i \end{matrix} \right),\vert AX_1 \vert=\sqrt{3},\vert AX_2 \vert=\sqrt{6}\\ &令P=\left( \frac{AX_1}{\vert AX_1\vert},\frac{AX_2}{\vert AX_2\vert} \right)=\left( \begin{matrix} \frac{i}{\sqrt{3}}&\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{3}}&\frac{i}{\sqrt{6}}\\ \frac{i}{\sqrt{3}}&\frac{i}{\sqrt{6}}\\ \end{matrix} \right),则正SVD\\ &A=P\Delta Q^H=\left( \begin{matrix} \frac{i}{\sqrt{3}}&\frac{2}{\sqrt{6}}\\ \frac{1}{\sqrt{3}}&\frac{i}{\sqrt{6}}\\ \frac{i}{\sqrt{3}}&\frac{i}{\sqrt{6}}\\ \end{matrix} \right)\left( \begin{matrix} \sqrt{3}&0\\ 0&\sqrt{6}\\ 0&0 \end{matrix} \right)\left( \begin{matrix} 1&0\\ 0&1 \end{matrix} \right) \end{aligned}$ $\begin{aligned} &令W=(P,P_1)=\left( \begin{matrix} \frac{i}{\sqrt{3}}&\frac{2}{\sqrt{6}}&0\\ \frac{1}{\sqrt{3}}&\frac{i}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\ \frac{i}{\sqrt{3}}&\frac{i}{\sqrt{6}}&-\frac{1}{\sqrt{2}}\\ \end{matrix} \right),或\left( \begin{matrix} \frac{i}{\sqrt{3}}&\frac{2}{\sqrt{6}}&0\\ \frac{1}{\sqrt{3}}&\frac{i}{\sqrt{6}}&\frac{i}{\sqrt{2}}\\ \frac{i}{\sqrt{3}}&\frac{i}{\sqrt{6}}&-\frac{i}{\sqrt{2}}\\ \end{matrix} \right),\\ &有SVD，A=\left( \begin{matrix} \frac{i}{\sqrt{3}}&\frac{2}{\sqrt{6}}&0\\ \frac{1}{\sqrt{3}}&\frac{i}{\sqrt{6}}&\frac{1}{\sqrt{2}}\\ \frac{i}{\sqrt{3}}&\frac{i}{\sqrt{6}}&-\frac{1}{\sqrt{2}}\\ \end{matrix} \right)\left( \begin{matrix} \sqrt{3}&0\\ 0&\sqrt{6}\\ 0&0 \end{matrix} \right)\left( \begin{matrix} 1&0\\ 0&1 \end{matrix} \right) \end{aligned}$

c. 当A是向量时

$\begin{aligned} &A=\left( \begin{matrix} a_1\\ \vdots\\ a_n \end{matrix} \right)\neq 0,则其正SVD \end{aligned}$ $\begin{aligned} &A^HA=\left(\overline{a_1},\cdots,\overline{a_n}\right)\left( \begin{matrix} a_1\\ \vdots\\ a_n \end{matrix} \right)=\vert a_1\vert^2+\cdots+\vert a_n\vert^2>0\\ &\lambda_1=\vert a_1 \vert^2+\cdots+\vert a_n\vert^2，令\Delta=\left(\sqrt{\lambda_1}\right),Q=(1)\\ &X_1=(1)，P=\frac{1}{\sqrt{\vert a_1 \vert^2+\vert a_2 \vert^2+\cdots+\vert a_n \vert^n}}\left( \begin{matrix} a_1\\\vdots\\a_n \end{matrix} \right),\\ &正SVD：A=P\Delta Q^H=\\ &\frac{1}{\sqrt{\vert a_1 \vert^2+\vert a_2 \vert^2+\cdots+\vert a_n \vert^n}}\left( \begin{matrix} a_1\\\vdots\\a_n \end{matrix} \right)\left(\sqrt{\vert a_1 \vert^2+\vert a_2 \vert^2+\cdots+\vert a_n}\right)\left(1\right) \end{aligned}$

d. $A^H$与A的SVD只需求一个

$若已知正SVD，A=P\Delta Q^H,可得A^H的正SVD=(P\Delta Q^H)^H$ $\begin{aligned} A=\left( \begin{matrix} 2&0&0\\ 3&0&0 \end{matrix} \right)与B=A^H的正SVD与SVD \end{aligned}$

2.1.3 正SVD的等价写法

$\begin{aligned} &A=P\Delta Q^H,\Delta=\left( \begin{matrix} s_1&&\\ &\ddots&\\ &&s_r \end{matrix} \right),令P=\left(\frac{AX_1}{\vert AX_1\vert},\cdots,\frac{AX_r}{\vert AX_r\vert} \right)=\left(p_1,\cdots,p_r\right)\\ &Q=\left(X_1,\cdots,X_r\right)=\left(q_1,\cdots,q_r\right),则有正SVD\\ &A=s_1p_1q_1^H+\cdots+s_rp_rq_r^H \end{aligned}$

2.2 QR分解

2.2.1 Schmidt正交化

设有3个n阶向量 $\alpha_1,\alpha_2,\alpha_3$ 线性无关

$\begin{aligned} 令&\beta_1=\alpha_1\\ &\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{\vert \beta_1\vert^2}\beta_1\\ &\beta_3=\alpha_3-\frac{(\alpha_3,\beta_2)}{\vert \beta_2\vert^2}\beta_2-\frac{(\alpha_3,\beta_1)}{\vert \beta_1\vert^2}\beta_1 \end{aligned}$

用 Schmidt 正交化方法可构造半U阵 $Q=\left(\frac{\beta_1}{\vert \beta_1\vert},\frac{\beta_2}{\vert \beta_2\vert},\frac{\beta_3}{\vert \beta_3\vert}\right)$ 是半U阵，可知 $Q^HQ=I$

2.2.2 QR分解

a. 定义

高阵

设 $A=\left(\alpha_1,\cdots,\alpha_p\right)_{n\times p}$ 为列无关(高阵)，则有分解 $A=QR$，其中 $Q=\left(\epsilon_1,\cdots,\epsilon_p \right)_{n\times p}$ 为半U阵，$R=\left(\begin{matrix}b_1&&*\\&\ddots&\\0&&b_p\end{matrix}\right)$ 是上三角, 且 $b_i>0$

Q阵求法
由Schmidt公式，产生正交向量组 $\beta_1,\beta_2,\cdots,\beta_p$ ，单位化可得 $\epsilon_1=\frac{\beta_1}{\vert \beta_1\vert},\cdots,\epsilon_p=\frac{\beta_p}{\vert \beta_p\vert}$ ，则 $Q$ 是半U阵，$Q^HQ=I$
R阵求法
$A=QR$ ，则 $Q^HA=Q^HQR=R\Rightarrow R=Q^HA$

方阵

任一方阵 $A=\left(\alpha_1,\cdots,\alpha_n\right)$ ，有 $A=QR$ ，其中 $Q=Q_{n\times n}$ 是U阵，$R=\left(\begin{matrix}b_1&&*\\&\ddots&\\0&&b_p\end{matrix}\right)$ 是上三角，且 $b_i>0$

b. QR分解步骤

先用 Schmidt 公式，求优阵Q或半优阵Q
在用 $R=Q^HA$，求上三角阵R
写出分解 $A=QR$

$\begin{aligned} &A=\left( \begin{matrix} 1&2i\\ i&1\\ i&0 \end{matrix} \right)=\left(\alpha_1,\alpha_2\right)，求QR分解 \end{aligned}$ $\begin{aligned} &\beta_1=\alpha_1=\left( \begin{matrix} 1\\i\\i \end{matrix} \right),\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{\vert \beta_1 \vert^2}\beta_1=\frac{1}{3}\left( \begin{matrix} 5i\\4\\1 \end{matrix} \right)\\ &\epsilon_1=\frac{\beta_1}{\vert \beta_1 \vert}=\frac{1}{\sqrt{3}}\left( \begin{matrix} 1\\i\\i \end{matrix} \right),\epsilon_2=\frac{\beta_2}{\vert \beta_2\vert}=\frac{1}{\sqrt{42}}\left( \begin{matrix} 5i\\4\\1 \end{matrix} \right),\\ &令Q=\left(\epsilon_1,\cdots,\epsilon_2\right)=\left( \begin{matrix} \frac{1}{\sqrt{3}}&\frac{5i}{\sqrt{42}}\\ \frac{i}{3}&\frac{4}{\sqrt{42}}\\ \frac{i}{3}&\frac{1}{\sqrt{42}} \end{matrix} \right)为半U阵\\ &R=Q^HA=\left( \begin{matrix} \frac{1}{\sqrt{3}}&\frac{-i}{3}&\frac{-i}{3}\\ \frac{-5i}{\sqrt{42}}&\frac{4}{\sqrt{42}}&\frac{1}{\sqrt{42}}\\ \end{matrix} \right)A=\left( \begin{matrix} \sqrt{3}&\frac{i}{\sqrt{3}}\\ 0&\frac{\sqrt{14}}{\sqrt{3}} \end{matrix} \right)为上三角,\\ &可得A=QR=\left( \begin{matrix} \frac{1}{\sqrt{3}}&\frac{5i}{\sqrt{42}}\\ \frac{i}{3}&\frac{4}{\sqrt{42}}\\ \frac{i}{3}&\frac{1}{\sqrt{42}} \end{matrix} \right)\left( \begin{matrix} \sqrt{3}&\frac{i}{\sqrt{3}}\\ 0&\frac{\sqrt{14}}{\sqrt{3}} \end{matrix} \right) \end{aligned}$

c. 例题

方阵

$\begin{aligned} &A=\left( \begin{matrix} 1&i\\ i&1 \end{matrix} \right)=\left(\alpha_1,\alpha_2\right) \end{aligned}$ $\begin{aligned} &令\beta_1=\alpha_1=\left( \begin{matrix} 1\\i \end{matrix} \right),\vert \beta_1\vert^2=2,\vert \beta_1\vert=\sqrt{2}\\ &\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{\vert \beta_1\vert^2}\beta_1=\left( \begin{matrix} i\\1 \end{matrix} \right)\\ &单位化，令\epsilon_1=\frac{\beta_1}{\vert \beta_1\vert}=\frac{1}{\sqrt{2}}\beta_1,\epsilon_2=\frac{\beta_2}{\vert \beta_2\vert}=\frac{1}{\sqrt{2}}\beta_2\\ &令Q=\left( \begin{matrix} \epsilon_1,\epsilon_2 \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{i}{\sqrt{2}}\\ \frac{i}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{matrix} \right),R=Q^HA=\left( \begin{matrix} \sqrt{2}&0\\ 0&\sqrt{2} \end{matrix} \right)\\ &可得A=QR=\left( \begin{matrix} \frac{1}{\sqrt{2}}&\frac{i}{\sqrt{2}}\\ \frac{i}{\sqrt{2}}&\frac{1}{\sqrt{2}} \end{matrix} \right)\left( \begin{matrix} \sqrt{2}&0\\ 0&\sqrt{2} \end{matrix} \right) \end{aligned}$

列高阵

$\begin{aligned} &A=\left( \alpha_1,\alpha_2,\alpha_3 \right)=\left( \begin{matrix} 1&-1&4\\ 1&4&-2\\ 1&4&2\\ 1&-1&0 \end{matrix} \right)_{4\times 3},求A=QR \end{aligned}$ $\begin{aligned} &令\beta_1=\alpha_1=\left( \begin{matrix} 1\\1\\1\\1 \end{matrix} \right),\vert \beta_1\vert^2=4,\vert \beta_1\vert=2\\ &\beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{\vert \beta_1\vert^2}\beta_1=\frac{5}{2}\left( \begin{matrix} -1\\1\\1\\-1 \end{matrix} \right),\vert \beta_2\vert=5,\\ &\beta_3=\alpha_3-\frac{(\alpha_3,\beta_2)}{\vert \beta_2\vert^2}\beta_2-\frac{(\alpha_3,\beta_1)}{\vert \beta_1\vert^2}\beta_1=2\left( \begin{matrix} 1\\-1\\1\\-1 \end{matrix} \right),\vert \beta_3\vert=4\\ &\epsilon_1=\frac{\beta_1}{\vert \beta_1\vert}=\frac{1}{2}\left( \begin{matrix} 1\\1\\1\\1 \end{matrix} \right),\epsilon_2=\frac{\beta_2}{\vert \beta_2\vert}=\frac{1}{2}\left( \begin{matrix} -1\\1\\1\\-1 \end{matrix} \right),\epsilon_3=\frac{\beta_3}{\vert \beta_3\vert}=\frac{1}{2}\left( \begin{matrix} 1\\-1\\1\\-1 \end{matrix} \right)\\ & 令Q=\left(\epsilon_1,\epsilon_2,\epsilon_3\right)=\frac{1}{2}\left( \begin{matrix} 1&-1&1\\ 1&1&-1\\ 1&1&1\\ 1&-1&-1 \end{matrix} \right),为半U阵.R=Q^HA=\left( \begin{matrix} 2&3&2\\ 0&5&-2\\ 0&0&4 \end{matrix} \right)\\ &则A=QR=\frac{1}{2}\left( \begin{matrix} 1&-1&1\\ 1&1&-1\\ 1&1&1\\ 1&-1&-1 \end{matrix} \right)\left( \begin{matrix} 2&3&2\\ 0&5&-2\\ 0&0&4 \end{matrix} \right) \end{aligned}$

d. *QR分解证明

$\begin{aligned} &有Schmidt公式，可将A的列向量写为:\\ &\left\{ \begin{aligned} &\quad\beta_1=\alpha_1\\ &\quad \beta_2=\alpha_2-\frac{(\alpha_2,\beta_1)}{\vert \beta_1\vert^2}\beta_1\\ &\quad\vdots\\ &\quad\beta_p=\alpha_p-\frac{(\alpha_p,\beta_1)}{\vert \beta_1\vert^2}\beta_1-\cdots-\frac{(\alpha_p,\beta_{p-1})}{\vert \beta_{p-1}\vert^2}\beta_{p-1}\\ \end{aligned} \right.\\ &可知 \alpha向量组与\beta向量组可互相表出：\\ &\left\{ \begin{aligned} &\quad\alpha_1=\beta_1\\ &\quad\alpha_2=(*)\beta_1+\beta_2\\ &\quad\vdots\\ &\quad\alpha_p=(*)\beta_1+(*)\beta_2+\cdots+\beta_p \end{aligned} \right.\\ &\Rightarrow \left(\alpha_1,\cdots,\alpha_p\right)=\left(\beta_1,\beta_2,\cdots,\beta_p\right)\left( \begin{matrix} 1&*&\cdots&*\\ 0&1&\cdots&*\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1 \end{matrix} \right)\\ &若将\beta向量组单位化：\epsilon_1=\frac{\beta_1}{\vert \beta_1\vert},\epsilon=\frac{\beta_2}{\vert \beta_2\vert},\cdots,\epsilon_p=\frac{\beta_p}{\vert \beta_p\vert}\\ &则\left(\beta_1,\beta_2,\cdots,\beta_p\right)=\left( \vert \beta_1\vert\epsilon_1,\vert \beta_2\vert\epsilon_2,\cdots,\vert \beta_p\vert\epsilon_p \right)\\ &=\left(\epsilon_1,\epsilon_2,\cdots,\epsilon_p\right)\left( \begin{matrix} \vert \beta_1\vert &&\\ &&\vert \beta_2\vert& \\ &&&\ddots&\\ &&&&\vert \beta_p\vert \end{matrix} \right)\\ &故A=\left(\beta_1,\beta_2,\cdots,\beta_p\right)\left( \begin{matrix} 1&*&\cdots&*\\ 0&1&\cdots&*\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1 \end{matrix} \right)\\ &=\left(\epsilon_1,\epsilon_2,\cdots,\epsilon_p\right)\left( \begin{matrix} \vert \beta_1\vert &&\\ &&\vert \beta_2\vert& \\ &&&\ddots&\\ &&&&\vert \beta_p\vert \end{matrix} \right)\left( \begin{matrix} 1&*&\cdots&*\\ 0&1&\cdots&*\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&1 \end{matrix} \right)\\ &=\left(\epsilon_1,\epsilon_2,\cdots,\epsilon_p\right)\left( \begin{matrix} \vert \beta_1\vert&*&\cdots&*\\ 0&\vert \beta_2\vert&\cdots&*\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&\vert \beta_p\vert \end{matrix} \right)\\ &=QR \end{aligned}$

e. QR分解的平移性质

若方阵 $A_{n\times n}$ 不可逆$(\vert A\vert =0)$，令 $A_{\epsilon}=(A+\epsilon I),A_{\epsilon}$ 可逆 $\Rightarrow A_\epsilon=Q_\epsilon R_{\epsilon}$ ，若 $\epsilon\rightarrow 0\Rightarrow A=QR$ ，$Q$ 为U阵，$R$ 为上三角阵

2.3 正定阵分解

a. $A=P^HP$

定理：$A>0\iff A=P^HP(P可逆)=PP^H(P可逆)$

$\Rightarrow$

若 $A$ 是正定阵，则 $A$ 必是Hermite阵，$A$ 的特征值是正实数。

又 $\because$ 正定阵一定与单位阵合同，即 $A\overset{\Delta}{=}\Lambda=\sqrt{\Lambda}I\sqrt{\Lambda}$ ,

令 $P=\sqrt{\Lambda}$ ，可知 $P$ 可逆，且 $P^H=P$

得证结论，$A>0\Rightarrow A=P^HP=PP^H$

$\Leftarrow$

若 $A=P^HP=P^HIP$ ，由于 $P$ 可逆，则 $A\overset{\Delta}{=}I>0$ ，则 $A$ 是正定阵
由二次型 $X^HAX=X^HP^HPX=(PX)^H(PX)=\vert PX\vert^2>0$ ，为正定二次型 $\therefore A$ 是正定阵

b. 平方根定理

$A>0\Rightarrow \exists B>0$ ，使得 $A=B\cdot B=B^2$

证明：

$\exists B,使得A=B\cdot B$
$\begin{aligned} &\because A>0，则A^H=A，\\ &由Hermite分解定理\Rightarrow 存在U阵Q，使得Q^HAQ=\Lambda\\ &=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\quad\\ &\quad&\lambda_n \end{matrix} \right)=\left( \begin{matrix} \sqrt{\lambda_1}\quad&\quad\\ &\ddots&\quad\\ &\quad&\sqrt{\lambda_n} \end{matrix} \right)^2=\Lambda'^2,\quad(\lambda_i > 0)\\ &而A=Q\Lambda Q^H=Q\sqrt{\Lambda}\sqrt{\Lambda}Q^H=Q\sqrt{\Lambda}Q^HQ\sqrt{\Lambda}Q^H\\ &令B=Q\sqrt{\Lambda}Q^H，则A=B^2 \end{aligned}$
$B是正定Hermite阵$
由Hermite分解定理，$\exists$ U阵 $Q$ ，使得 $Q^HAQ=\Lambda=\left( \begin{matrix} \sqrt{\lambda_1}&\\ &\ddots&\\ &&\sqrt{\lambda_n} \end{matrix} \right)^2=\Lambda’^2,\Lambda’=\sqrt{\Lambda}>0$ ，为正定阵
已知 $Q^H\sqrt{\Lambda}Q=B$ ，即 $B\overset{\Delta}{=}\sqrt{\Lambda}>0$ ，$B$ 为正定阵

平方根公式

$\begin{aligned} &B=\sqrt{A}=Q\left( \begin{matrix} \sqrt{\lambda_1}&&\\ &\ddots&\\ &&\sqrt{\lambda_n} \end{matrix} \right)Q^H \end{aligned}$

c. 乔利斯分解——正定阵的QR分解

若 $A>0(正定)$ ，则有 $A=R^HR$ ，其中 $R=\left(\begin{matrix}b_1&&*\\&\ddots&\\0&&b_n\end{matrix}\right)$ 为上三角阵，且 $b_1>0,\cdots,b_n>0$ ，则 $A=R^HR$ 为乔利斯分解

证明

$\begin{aligned} &A>0必有可逆阵P，使A=P^HP,对P使用QR分解，其中R为上三角，Q为U阵\\ &\Rightarrow A=P^HP=(QR)^H(QR)=R^H(Q^HQ)R=R^HR\\ &可写分解：A=R^HR,R=\left( \begin{matrix} b_1&&*\\ &\ddots&\\ 0&&b_n \end{matrix} \right)为上三角，且b_1>0,\cdots,b_n>0 \end{aligned}$

d. 平方根分解

$A>0(正定)$ ，则有 $A=B^2,B>0(正定)$ ，且矩阵 $B$ 唯一，可写 $B=\sqrt{A},A=(\sqrt{A})^2$

证明

$\begin{aligned} &对A>0，必有Hermite分解(Q为U阵)：\\ &A=Q\Lambda Q^H,其中\Lambda=\left( \begin{matrix} \lambda_1&&0\\ &\ddots&\\ 0&&\lambda_n \end{matrix} \right),\lambda_i>0\\ &令\sqrt{\Lambda}=\left( \begin{matrix} \sqrt{\lambda_1}&&0\\ &\ddots&\\ 0&&\sqrt{\lambda_n} \end{matrix} \right),且\sqrt{\Lambda}为正定阵\\ &令B=Q\sqrt{\Lambda}Q^H\Rightarrow B为正定Hermite阵(\lambda(B)>0)\\ &B^2=(Q\sqrt{\Lambda}Q^H)(Q\sqrt{\Lambda}Q^H)=Q\Lambda Q^H=A \end{aligned}$

2.4 单阵

单阵 $A$（又叫单纯阵，可对角阵），即满足 $P^{-1}AP=D=\left(\begin{matrix}\lambda_1&&0\\&\ddots&\\0&&\lambda_n\end{matrix}\right)$ ， $P$ 可逆， $P$ 中列向量为 $A$ 的特征向量

2.4.1 单阵谱公式

若 $A$ 为单阵，全体不同特征根为 $\lambda_1,\lambda_2,\cdots,\lambda_k$ ，则有 $A=\lambda_1G_1+\cdots+\lambda_kG_k$ 为 $A$ 的谱分解

满足性质：

谱阵： $G_i=\frac{(A-\lambda_1)\cdots(A-\lambda_{i-1})(A-\lambda_{i+1})\cdots(A-\lambda_k)}{(\lambda_i-\lambda_1)\cdots(\lambda_i-\lambda_{i-1})(\lambda_i-\lambda_{i+1})\cdots(\lambda_i-\lambda_k)}$，谱阵 $G_1,\cdots,G_k$ 中各列都是A的特征向量
和为单位阵： $G_1+G_2+\cdots+G_k=I$
相互正交： $G_1G_2=0,\cdots,G_iG_j=0(i\neq j)$
幂等： $G_1^2=G_1,\cdots,G_k^2=G_k$ ，但 $G_1^H=G_1,\cdots,G_k^H=G_k$ 不一定成立

a. 单阵谱函数

$f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k$

幂次

$A^p=\lambda_1^pG_1+\cdots+\lambda_k^pG_p,p=0,1,…$

$A=\left(\begin{matrix} 3&1\\2&2 \end{matrix}\right),求A^{100}$ $\begin{aligned} &由A是行和相等矩阵，所以行和4为特征值，\lambda(A)=\{4,tr(A)-4\}=\{4,1\}\\ &故二阶阵有2个不同特征值，所以必为单阵\\ &G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{3}\left( \begin{matrix} 2&1\\2&1 \end{matrix} \right),G_2=-\frac{1}{3}\left( \begin{matrix} 1&-1\\-2&2 \end{matrix} \right)\\ &可知A^{100}=4^{100}G_1+1^{100}G_2=\\ &本例中，特向\left( \begin{matrix} 1\\1 \end{matrix} \right),\left( \begin{matrix} 1\\-2 \end{matrix} \right)不正交，不是正规阵 \end{aligned}$

单阵逆公式

$A^{-1}=\frac{1}{\lambda_1}G_1+\frac{1}{\lambda_2}G_2+\cdots+\frac{1}{\lambda_k}G_k$ ，其中 $A$ 为单阵

b. 单阵函数公式

若 $f_1(x),f_2(x),\cdots,f_k(x)$ 为 $x$ 的 $k-1$ 次多项式，且 $f_1(x)+f_2(x)+\cdots+f_k(x)=1$ ，则 $f_1(A)+f_2(A)+\cdots+f_k(A)=I$ ，$f_1(A),\cdots,f_k(A)$ 中非0列都是 $A$ 的特征向量

2.4.2 单阵判定

a. 充分条件

若存在可逆阵 $P$ ，使 $A$ 相似于对角阵，则 $A$ 为单阵

$P^{-1}AP=D=\left(\begin{matrix}\lambda_1&&\\&\ddots\\&&\lambda_k\end{matrix}\right)$

单阵特例
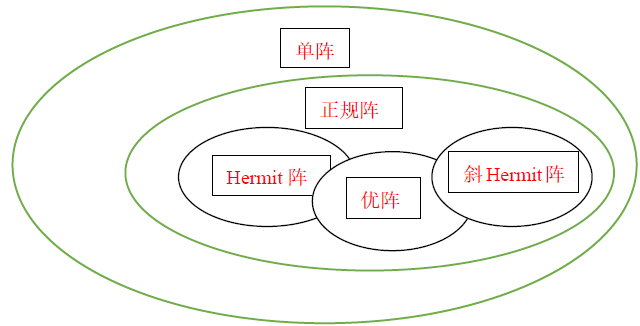
$A$ 为正规阵，则 $A$ 必相似于对角阵
证： $A$ 为正规阵，则存在U阵 $Q$ 使 $Q^HAQ= \Lambda$ ，使A阵U相似于对角阵，故正规阵一定是单阵
设 $n$ 阶方阵 $A$ 恰有 $n$ 个不同根 $\lambda_1,\cdots,\lambda_n$ ，则 $A$ 为单阵（必相似于对角阵）
$\begin{aligned} 证明：&\\ &\lambda(A)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\} ，则有AX_i=\lambda_i X_i ,令P=(X_1,X_2,\cdots,X_n),X_i为n维列向量\\ &A(X_1,X_2,\cdots,X_n)=(\lambda_1X_1,\lambda_2X_2,\cdots,\lambda_nX_n)=(X_1,X_2,\cdots,X_n)\left(\begin{matrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{matrix}\right)\\ &\Rightarrow AP=PD\iff P^{-1}AP=D \end{aligned}$
A有 $n$ 个无关的特征向量 $X_1,X_2,\cdots,X_n$
令 $P=\left(X_1,X_2,\cdots,X_n\right) \Rightarrow P^{-1}AP=D$
若每个 $k$ 重根 $\lambda$ ，恰有 $k$ 个特征向量，则 $A$ 为单阵
- 方程 $(A-\lambda_1)X=0$ 有 $n-r(A-\lambda_1I)$ 个基本解 $\Rightarrow AX=\lambda_1X 有n-r(A-\lambda_1I)个基本解$
  常通过判断 $r(A-重根I)$ 判断A是否为单阵
  $\Rightarrow r(A-\lambda_1I)=n-k$ ，$\lambda_1$ 有k个特征向量，则A可能是单阵
  $\Rightarrow r(A-\lambda_1I)\neq n-k$ ，则A必不是单阵
- eg1
  $A=\left(\begin{matrix} 1&1&0\\0&2&0\\0&0&1 \end{matrix}\right),\lambda(A)=\{2,1,1\} ，\lambda_1=1为2重根$
  验证A是否为单阵：
  $\begin{aligned} A-1I=\left( \begin{matrix} 0&1&0\\0&1&0\\0&1&0 \end{matrix} \right),r(A-I)=1=3-2\,\therefore A是单阵 \end{aligned}$
- eg2
  $A=\left(\begin{matrix} 1&1&0\\0&1&0\\0&0&2 \end{matrix}\right),\lambda(A)=\{2,1,1\} ，\lambda_1=1为2重根$
  验证A是否为单阵：
  $A-1I=\left( \begin{matrix} 0&1&0\\0&0&0\\0&0&1 \end{matrix} \right),r(A-I)=2 \neq 3-2=1,\therefore A不是单阵$
设 $\lambda_1,\lambda_2,\cdots,\lambda_k$ 为A的全体不同根
Cayley定理：
若方阵 $A$ 的特征多项式 $T(x)=\vert A-x I\vert=c_0+c_1x+c_2x^2+\cdots+c_nx^n$ ，则 $T(A)=c_0I+c_1A+c_2A^2+\cdots+c_nA^n=0$
- 方阵A的特征多项式可分解为 $T(x)=(x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_n)$ 满足 $T(A)=(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_nI)=0$
若 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)=0$ ，则 $A$ 为单阵( $A$ 相似于对角阵)
若 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)\neq 0$ ，则 $A$ 不是单阵
eg
上述判定方法也适用于分块阵

b. 单阵充要条件：0化式判别法(了解，判断用重根矩阵秩)

$A为单阵\iff 极小式m(x)无重根；若m(x)有重根，则A不是单阵$

0化式与极小式定义

若多项式 $f(x)$ 使 $f(A)=0$ ，则称 $f(x)$ 为 $A$ 的0化式

极小式为次数最少的0化式 ：若 $\lambda_1,\cdots,\lambda_k$ 为不同根，且 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)=0$ ，则 $A$ 必为单阵，此时称 $m(x)=(x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_k)$ 为 $A$ 的极小式

eg1：
$\begin{aligned} &A=I=\left(\begin{matrix}1&0\\0&1\end{matrix}\right),满足A^2=I，可知f(x)=x^2-1=0,且f(A)=A^2-I=0\\ &f(x)=x^2-1=(x-1)(x+1)为A的0化式\\ &\because A-I=0,\therefore x-1也是A的0化式，且m(x)=x-1为极小式 \end{aligned}$
eg2:
$\begin{aligned} &A=\left( \begin{matrix} -1&0\\0&1 \end{matrix} \right)，A^2=I,即A^2-I=0,\\ &f(x)=x^2-1=(x-1)(x+1)为A的0化式，但由于A-I\neq 0且A+I \neq 0\\ &故A的极小式m(x)=x^2-1 \end{aligned}$
极小式求法

对于 $\vert xI-A \vert=(x-a)^2(x-b)=0$
- 若 $(A-aI)(A-bI)=0$ ，则极小式为 $m(x)=(x-a)(x-b)$
- 若 $(A-aI)(A-bI)\neq 0$ ，则极小式为 $m(x)=(x-a)^2(x-b)$
对于 $\vert xI-A \vert=(x-a)(x-b)(x-c)$ ，则极小式为 $m(x)=(x-a)(x-b)(x-c)$

若f(x)=0无重根，且f(A)=0,则A必为单阵

定理：

若 $f(A)=0$ ，则 $f(A)g(A)=0$ ,可知 $f(x)g(x)$ 也是0化式
特征多项式 $f(x) = \vert xI-A \vert=a_0+a_1x+a_2x^2+\cdots+a_nx^n$ 一定是0化式，即 $f(A)=a_0+a_1A+\cdots+a_nA^n=0$
极小式为特征多项式的因式，可表示为 $\vert xI-A \vert=m(x)g(x)$
极小式必为每个0化式 $f_i(x)$ 的因子，即若 $f_i(A)=0$ ，则 $f_i(x)=m(x)g_i(x)$

应用

列出特征方程，求出极小式，即证明A是单阵
根据极小式，写出单阵谱分解
计算f(A)

$A=\left( \begin{matrix} 2&2&1\\1&3&1\\1&2&2 \end{matrix} \right)，求A的谱分解p$ $\begin{aligned} &\begin{matrix} \vert A-\lambda I\vert=(x-5)(x-1)^2,且(A-5I)(A-I)=0\Rightarrow A为单阵 \end{matrix}\\ &\Rightarrow 单阵A有谱分解A=5G_1+G_2= \end{aligned}$

$A=\left( \begin{matrix} 1&1&0\\0&2&0\\0&0&3 \end{matrix} \right),求谱分解\\ A为上三角阵，所以A有三个互异特征根1,2,3，极小式为 (x-1)(x-2)(x-2)=0\\ 故A由谱分解A=G_1+2G_2+3G_3$

2.4.3 正规阵

a. 定义

若方阵A满足 $A^HA=AA^H$ ，则A为正规阵
正规条件：$A^HA=AA^H$

b. 正规阵特点

正规阵必为方阵 ($A^HA与AA^H$ 的阶数相等，即行列数相等)
$A正规\iff A^H正规$ ，$A不正规\iff A^H不正规$

c. 常见正规阵

对角阵

对角阵 $A=\left(\begin{matrix}a_1&&\\&\ddots&\\&&a_n\end{matrix}\right)$ 必正规

三角正规阵必对角

若三角阵 $B=\left(\begin{matrix}b_{1}&b_{12}&\cdots&b_{1n}\\&b_{2}&\cdots&b_{2n}\\&&\ddots&\\&&&b_n\end{matrix}\right)$ 正规，则 $B=\left(\begin{matrix}b_1&&&\\&b_2&&\\&&\ddots&\\&&&b_n\end{matrix}\right)$ 为对角形

证明：严格三角阵不是正规阵

$\begin{aligned} &设B=\left( \begin{matrix} b_1&b_{12}&b_{13}\\ &b_2&b_{23}\\ &&b_{3} \end{matrix} \right)为正规阵，B^H=\left( \begin{matrix} \overline{b_1}&&\\ \overline{b_{12}}&\overline{b_2}&\\ \overline{b_{13}}&\overline{b_{23}}&\overline{b_3} \end{matrix} \right)\\ &BB^H=\left( \begin{matrix} b_1&b_{12}&b_{13}\\ &b_2&b_{23}\\ &&b_{3} \end{matrix} \right)\left( \begin{matrix} \overline{b_1}&&\\ \overline{b_{12}}&\overline{b_2}&\\ \overline{b_{13}}&\overline{b_{23}}&\overline{b_3} \end{matrix} \right)\\ &=\left( \begin{matrix} \vert b_1 \vert^2+\vert b_{12} \vert^2+\vert b_{13} \vert^2 &&\\ &\vert b_{23} \vert^2+\vert b_2 \vert^2&\\ &&\vert b_3 \vert^2 \end{matrix} \right)\\ &B^HB=\left( \begin{matrix} \overline{b_1}&&\\ \overline{b_{12}}&\overline{b_2}&\\ \overline{b_{13}}&\overline{b_{23}}&\overline{b_3} \end{matrix} \right)\left( \begin{matrix} b_1&b_{12}&b_{13}\\ &b_2&b_{23}\\ &&b_{3} \end{matrix} \right)\\ &=\left( \begin{matrix} \vert b_1\vert^2 &&\\ &\vert b_{12}\vert^2+\vert b_2\vert^2&\\ &&\vert b_{13}\vert^2+\vert b_{23}\vert^2+\vert b_{3}\vert^2 \end{matrix} \right),\\ &若B满足正规阵，则B^HB=BB^H,即\\ &\Rightarrow \left\{ \begin{aligned} \vert b_1\vert^2 = \vert b_1 \vert^2+\vert b_{12} \vert^2+\vert b_{13} \vert^2\\ \vert b_{12}\vert^2+\vert b_2\vert^2=\vert b_{23} \vert^2+\vert b_2 \vert^2\\ \vert b_3 \vert^2=\vert b_{13}\vert^2+\vert b_{23}\vert^2+\vert b_{3}\vert^2 \end{aligned} \right.\Rightarrow \left\{ \begin{aligned} \vert b_{12} \vert^2=0\\ \vert b_{13} \vert^2=0\\ \vert b_{23} \vert^2=0 \end{aligned} \right.\\ &\Rightarrow b_{12}=b_{13}=b_{23}=0，即B=\left( \begin{matrix} b_{1}&&\\ &b_{2}&\\ &&b_{3} \end{matrix} \right)为对角形 \end{aligned}$

若分块阵 $A=\left(\begin{matrix} B&C\\0&D \end{matrix}\right)$ 正规，则 $C=0$ ，且 $B，D$ 都正规，即 $A=\left(\begin{matrix} B&0\\0&D \end{matrix}\right)$

$\begin{aligned} &A^HA=\left( \begin{matrix} B^H&0\\ C^H&D^H \end{matrix} \right)\left( \begin{matrix} B&C\\ 0&D \end{matrix} \right)=\left( \begin{matrix} B^HB&B^HC\\ C^HB&C^HC+D^HD \end{matrix} \right)\\ &AA^H=\left( \begin{matrix} B&C\\ 0&D \end{matrix} \right)\left( \begin{matrix} B^H&0\\ C^H&D^H \end{matrix} \right)=\left( \begin{matrix} BB^H+CC^H&CD^H\\ DC^H&C^HC+DD^H \end{matrix} \right)\\ &由于tr(A^HA)=tr(AA^H),\therefore tr(CC^H)=0,\\ &利用迹公式可写tr(CC^H)=\sum \vert c_{i,j} \vert^2=0，其中C=(c_{i,j})，C为零阵\\ &且BB^H=B^HB,DD^H=D^HD \end{aligned}$

由证明过程可见，严格三角阵为非正规阵

H阵与斜H阵

Hermite阵与斜Hermite阵必正规

$\begin{aligned} 若A是Hermite阵，则A^H=A，A^HA=AA=AA^H \end{aligned}$

实对称阵与反对称阵都是正规阵

U阵

U阵必正规（实正交阵）

$\begin{aligned} A^HA=I=AA^H \end{aligned}$

e. 正规阵的构造方法

倍数法则

若 $A$ 正规，取倍数 $k$ ，则 $kA$ 为正规阵

$\begin{aligned} \left( \begin{matrix} 0&i&i\\ i&0&i\\ i&i&i \end{matrix} \right)=i\left( \begin{matrix} 0&1&1\\ 1&0&1\\ 1&1&1 \end{matrix} \right),\left( \begin{matrix} i&i\\ i&2i \end{matrix} \right)=i\left( \begin{matrix} 1&1\\1&2 \end{matrix} \right)都是正规阵\\ A=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)为正规U阵，则\sqrt{2}A=\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right) \end{aligned}$

平移法则

若 $A$ 正规，则 $A\pm cI$ 正规

$\begin{aligned} 若A是正规阵，则(A\pm cI)^H(A\pm cI)&=(A^H\pm cI)(A\pm cI)\\ &=A^HA\pm cA^H\pm cA+c^2I\\ &=AA^H\pm cA\pm cA^H+c^2I\\ &=(A\pm cI)(A^H\pm cI) \end{aligned}$

U相似

若 $A$ 正规，则 $Q^HAQ$ 也正规，其中 $Q$ 为U阵($Q^H=Q^{-1}$)，即正规阵的U相似阵一定正规

证明：

$\begin{aligned} &\because A^HA=AA^H，且存在U阵Q，使得Q^HAQ=B，即证B^HB=BB^H\\ &B^HB=(Q^HAQ)^H(Q^HAQ)=Q^HA^HQQ^HAQ=Q^HA^HAQ\\ &BB^H=(Q^HAQ)(QAQ^H)^H=Q^HAQQ^HA^HQ=Q^HAA^HQ\overset{AA^H=A^HA}{=}Q^HA^HAQ\\ &\therefore B^HB=BB^H,B为正规阵 \end{aligned}$

多项式正规

若 A 正规，则 $f(A)=\lambda_0I+\lambda_1A+\lambda_2A^2+\cdots+\lambda_nA^K$ 正规

f. 正规阵与其H阵的特征向量相同

若A正规，则 $A^H$ 与 A 有相同的向量

$\begin{aligned} 若A正规，且AX=\lambda X，则A^HX=\overline{\lambda}X \end{aligned}$

证明

$\begin{aligned} &只需证 (A^H-\overline{\lambda}I)X=0,即(A-\lambda I)^HX=0,由(A-\lambda I)X=0\\ &\vert A-\lambda I \vert^2=0\Rightarrow ((A-\lambda I)X)^H(A-\lambda I)X=0\Rightarrow X^H(A-\lambda I)^H(A-\lambda I)X=0\\ &由于A-\lambda I 正规，(A-\lambda I)^H(A-\lambda I)=(A-\lambda I)(A-\lambda I)^H\\ &即有 X^H((A-\lambda I)^H)^H(A-\lambda I)^HX=0\\ &\Rightarrow ((A-\lambda I)^HX)^H(A-\lambda I)^HX=\vert (A-\lambda I)^HX\vert^2=0\\ &\Rightarrow (A-\lambda I)^HX=0\Rightarrow (A^H-\overline{\lambda}I)X=0\Rightarrow A^HX=\overline{\lambda}X\\ &故结论得证，若A正规，则AX=\lambda X\iff A^HX=\overline{\lambda}X\\ &其中，若\lambda(A)=\{\lambda_1,\cdots,\lambda_n\},则\lambda(A^H)=\{\overline{\lambda_1},\cdots,\overline{\lambda_n}\} \end{aligned}$

2.4.4 正规分解定理

$正规阵\subset 单阵$
(相似对角化)若 $A=A_{n\times n}$ 正规，则存在U阵Q，使 $Q^HAQ=\Lambda=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)$

证明

$\begin{aligned} &设A=A_{n\times n} 正规，由U相似定理，Q^HAQ正规，由许尔公式，存在U阵Q，使\\ &Q^HAQ=D=\left( \begin{matrix} \lambda_1&&*\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)为上三角阵\\ &D=Q^HAQ为正规三角阵，由 "正规三角定理" 可知D为对角阵\\ &即Q^{-1}AQ=D=\left( \begin{matrix} \lambda_1&&\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)成立 \end{aligned}$

a. 正规阵A恰有n个正交特向

$\begin{aligned} &由Q^{-1} AQ=D=\left( \begin{matrix} \lambda_1&&\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)\Rightarrow AQ=QD\\&\Rightarrow A\left(q_1,\cdots,q_n\right)=\left(q_1,\cdots,q_n\right)D\\ &\Rightarrow\left(Aq_1,\cdots,Aq_n\right)=\left(\lambda_1q_1,\cdots,\lambda_nq_n\right)\\ &U阵Q为A的特征向量组成的矩阵，且n个特征向量相互正交，q_1\bot \cdots \bot q_n \end{aligned}$

b. 正规分解方法

先令特征根 $\lambda_1,\cdots,\lambda_n$ ，求正交特征向量 $X_1\bot \cdots \bot X_n$
令U阵 $Q=\left(q_1,\cdots,q_n\right)=\left(\frac{X_1}{\vert X_1\vert},\cdots,\frac{X_n}{\vert X_n \vert}\right)$
则有U相似阵 $Q^HAQ=D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)$ 为对角阵
可写正规分解 $A=QDQ^H$

定义法

对矩阵 $A=\left(\begin{matrix} 1&-1\\1&0\end{matrix}\right)$ 正规分解

$\begin{aligned} &A=\left( \begin{matrix} 1&-1\\ 1&0 \end{matrix} \right)为正规阵，计算可得\lambda_1=i,\lambda_2=-i，X_1=\left( \begin{matrix} i\\1 \end{matrix} \right),X_2=\left( \begin{matrix} 1\\i \end{matrix} \right),\\ &且X_1与X_2为不同特征值的特征向量，所以X_1\bot X_2\\ &令U阵Q=\left( \begin{matrix} \frac{X_1}{\vert X_1\vert},\frac{X_2}{\vert X_2\vert} \end{matrix} \right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right),可得Q^HAQ=D=\left( \begin{matrix} i&\\ &-i \end{matrix} \right)\\ &则有正规分解 A=QDQ^H=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)\left( \begin{matrix} i&\\ &-i \end{matrix} \right)\frac{1}{\sqrt{2}}\left( \begin{matrix} -i&1\\ 1&-i \end{matrix} \right) \end{aligned}$

平移法

$\begin{aligned} &令B=\left( \begin{matrix} 1&-1\\ 1&1 \end{matrix} \right)=I+A=\left( \begin{matrix} 1&\\ &1 \end{matrix} \right)+\left( \begin{matrix} 0&-1\\ 1&0 \end{matrix} \right),其中A为正规U阵\\ &\lambda(B)=\{\lambda_1,\lambda_2\}=\{1+i,1-i\},X_1=\left( \begin{matrix} i\\1 \end{matrix} \right),X_2=\left( \begin{matrix} 1\\i \end{matrix} \right),\\ &得U阵Q=\left(\frac{X_1}{\vert X_1\vert},\frac{X_2}{\vert X_2\vert}\right)=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)，故有正规分解A=QDQ^H\\ &=\frac{1}{\sqrt{2}}\left( \begin{matrix} i&1\\ 1&i \end{matrix} \right)\left( \begin{matrix} 1+i&\\ &1-i \end{matrix} \right)\frac{1}{\sqrt{2}}\left( \begin{matrix} -i&1\\ 1&-i \end{matrix} \right) \end{aligned}$

2.4.5 正规谱分解

a. 正规分解推导

$\begin{aligned} &若A=A_{n\times n} 正规，互异根为 \lambda_1,\cdots,\lambda_k，则有Q^HAQ=D=\left( \begin{matrix} \lambda_1I_1&&\\ &\ddots&\\ &&\lambda_kI_k \end{matrix} \right)\\ &其中Q为U阵，Q^H=Q^{-1},I_1,\cdots,I_k为单位阵\\ &\left(如D=\left( \begin{matrix} 2\left( \begin{matrix} 1&\\ &1 \end{matrix} \right)\\ &3\left( \begin{matrix} 1&\\ &1 \end{matrix} \right) \end{matrix} \right)=\left( \begin{matrix} 2I_1&\\ &3I_2 \end{matrix} \right)\right)\\ &可设 Q^{-1}AQ=D=\left( \begin{matrix} \lambda_1I_1&&0\\ &\ddots&\\ 0&&\lambda_kI_k \end{matrix} \right)(Q为U阵，Q^H=Q^{-1})\\ &写为D=\lambda_1\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right)+\lambda_2\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right)+\cdots+\lambda_k\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &则令D_1=\left( \begin{matrix} I_1&&0\\ &\ddots&\\ 0&&0 \end{matrix} \right),D_2=\left( \begin{matrix} 0&&0\\ &I_2&\\ 0&&\ddots \end{matrix} \right),\cdots,D_k=\left( \begin{matrix} 0&&0\\ &\ddots&\\ 0&&I_k \end{matrix} \right)\\ &\Rightarrow Q^{-1}AQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ \end{aligned}$

则可得出结论：

和为单位阵：$D_1+D_2+\cdots+D_k=\left( \begin{matrix} I_1&&\\ &\ddots&\\ &&I_k \end{matrix} \right)=I(单位阵)$
正交：$D_1D_2=0,\cdots,D_iD_j=0(i\neq j)$
幂等：$D_1^2=D_1,\cdots,D_k^2=D_k，且D_1^H=D_1,\cdots,D_k^H=D_k$

故可等价写为：

$\begin{aligned} &Q^HAQ=D=\lambda_1D_1+\lambda_2D_2+\cdots+\lambda_kD_k\\ &\Rightarrow A=QDQ^H=\lambda_1QD_1Q^H+\lambda_2QD_2Q^H+\cdots+\lambda_kQD_kQ^H\\ &可令G_1=QD_1Q^H,\cdots,G_k=QD_kQ^H\\ &\Rightarrow A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned}$

有类似推论：

$G_1+G_2+\cdots+G_k=I$
$\because G_1+G_2+\cdots+G_k=Q(D_1Q^{-1}+D_2+\cdots+D_k)Q^{-1}=QIQ^{-1}=I$
$G_1G_2=0,\cdots,G_iG_j=0(i \neq j)$
$\because G_1G_2=(QD_1Q^{-1})(QD_2Q^{-1})=0$
$G_1^2=G_1,\cdots,G_k^2=G_k$，且 $G_1^H=G_1,\cdots,G_k^H=G_k$ 都是Hermite阵

b. 正规阵谱分解与谱阵性质

若 $A=A_{n\times n}$ 正规，全体互异根为 $\lambda_1,\cdots,\lambda_k$，则有 $A=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k$ ，其中 $G_1,\cdots,G_k$ 为 $A$ 的谱阵

性质

$\begin{aligned} &①和为I：G_1+G_2+\cdots+G_k=I\\ &②正交：G_1G_2=0,\cdots,G_iG_j=0(i\neq j)\\ &③幂等： G_1^{2}=G_1,\cdots,G_k^{2}=G_k(幂等),且G_1^H=G_1,\cdots ,G_k^H=G_k\\ &④正规阵幂次：A^p=\lambda_1^pG_1+\cdots+\lambda_kG_k,p=0,1,2.\cdots\\ &⑤正规阵函数：f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k,f(x)=c_0+c_1x_1+\cdots+c_px^p\\ & \quad \because f(A)=c_0I+c_1A+\cdots+c_kA^p\\ & \quad \quad =c_0(G_1+\cdots+G_k)+c_1(\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k)+\\ & \quad \quad \quad \cdots+c_p(\lambda_1^pG_1+\lambda_2^pG_2+\cdots+\lambda_p^kG_k)\\ & \quad \quad =(c_0+c_1\lambda_1+c_p\lambda_1^k)G_1+(c_0+c_1\lambda_2+\cdots+c_p\lambda_2^pk)G_2+\\ & \quad \quad \quad \cdots+(c_0+c_1\lambda_k+\cdots+c_p\lambda_k^p)G_k\\ & \quad \quad =f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k\\ &⑥正规阵求法：设A正规，全体不同根为 \lambda_1,\lambda_2,\cdots,\lambda_k，则有谱阵公式G_1,G_2,\cdots,G_k\\ &\quad G_1=\frac{(A-\lambda_2I)\cdots(A-\lambda_kI)}{(\lambda_1-\lambda_2)\cdots(\lambda_1-\lambda_k)},G_2=\frac{(A-\lambda_1I)(A-\lambda_3I)\cdots(A-\lambda_kI)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)\cdots(\lambda_2-\lambda_k)}\\ &\quad\cdots\\ &\quad G_k=\frac{(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_{k-1}I)}{(\lambda_k-\lambda_1)(\lambda_k-\lambda_2)\cdots(\lambda_k-\lambda_{k-1})}\\ &⑦谱阵中列是A的特征向量：AG_1=\lambda_1G_1,AG_2=\lambda_2G_2,\cdots,AG_k=\lambda_kG_k\\ &\quad \because AG_1=(\lambda_1G_1+\cdots+\lambda_kG_k)G_1=\lambda_1G_1 \end{aligned}$

谱阵求法

由推论⑤可知，取k个不同的函数f(x)可求出谱阵 $G_1,G_2,\cdots.G_k$

证明：

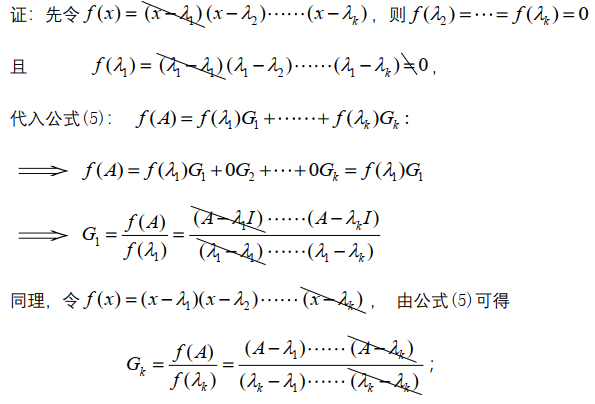
A正规有2个不同根

$\begin{aligned} G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2},G_2=I-G_1=\frac{A-\lambda_1I}{\lambda_2-\lambda_1} \end{aligned}$

A正规且有3个不同根

$\begin{aligned} &G_1=\frac{(A-\lambda_2I)(A-\lambda_3I)}{(\lambda_1-\lambda_2)(\lambda_1-\lambda_3)},G_2=\frac{(A-\lambda_1I)(A-\lambda_3I)}{(\lambda_2-\lambda_1)(\lambda_2-\lambda_3)},\\ &G_3=I-G_1-G_2=\frac{(A-\lambda_1I)(A-\lambda_2I)}{(\lambda_3-\lambda_1)(\lambda_3-\lambda_2)} \end{aligned}$

正规分解性质的应用例

1

$\begin{aligned} A=\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right)(实对称正规阵)，求A与f(A)的谱分解，与A^{100} \end{aligned}$ $\begin{aligned} &可知A为秩1矩阵，r(A)=1,特征根为\lambda(A)={5,0,0},不同根为\lambda_1=5,\lambda_2=0\\ &G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{5}\left( \begin{matrix} 1&0&-2\\ 0&0&0\\ -2&0&4 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=I-G_1=\frac{1}{5}\left( \begin{matrix} 4&0&2\\ 0&5&0\\ 2&0&1 \end{matrix} \right)\\ &得谱分解：A=\lambda_1G_1+\lambda_2G_2,且f(A)=f(\lambda_1)G_1+f(\lambda_2)G_2\\ &即f(A)=f(5)G_1+f(0)G_2\\ &令f(x)=x^{100}\Rightarrow A^{100}=f(5)G_1+f(0)G_2=5^{100}G_1=5^{100}\frac{1}{5}A=5^{99}A\\ &由于G中列向量都是A的特征向量，所以\lambda_1=5的特征向量\alpha_1=\left( \begin{matrix} 1\\0\\-2 \end{matrix} \right)\\ &\lambda_2=0的特征向量\alpha_2=\left( \begin{matrix} 2\\0\\1 \end{matrix} \right),\alpha_3=\left( \begin{matrix} 0\\1\\0 \end{matrix} \right) \end{aligned}$

2 2.分块法

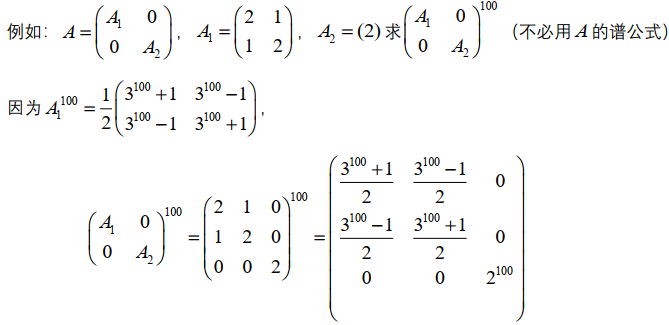
c. 新平方根公式

$\begin{aligned} &\sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_n}G_n\\ &条件：A正规，且A=\lambda_1G_1+\cdots+\lambda_kG_k \end{aligned}$

证明：

$\begin{aligned} (\sqrt{A})^2&=(\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2+\cdots+\sqrt{\lambda_k}G_k)^2\\ &=\lambda_1G_1^2+\lambda_2G_2^2+\cdots+\lambda_kG_k^2\\ &=\lambda_1G_1+\lambda_2G_2+\cdots+\lambda_kG_k \end{aligned}$

eg

$A=\left( \begin{matrix} 5&4\\ 4&5 \end{matrix} \right),求\sqrt{A}$

$\begin{aligned} &由于A为行和相等矩阵，\therefore \lambda(A)=\{9,tr(A)-9\}=\{9,1\},令\lambda_1=9,\lambda_2=1\\ &\Rightarrow G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{2}\left( \begin{matrix} 1&1\\1&1 \end{matrix} \right),G_2=\frac{A-\lambda_1I}{\lambda_2-\lambda_1}=\frac{1}{2}\left( \begin{matrix} 1&-1\\-1&1 \end{matrix} \right)\\ &\Rightarrow \sqrt{A}=\sqrt{\lambda_1}G_1+\sqrt{\lambda_2}G_2=3G_1+G_2=\left( \begin{matrix} 2&1\\1&2 \end{matrix} \right) \end{aligned}$

2.5 高低分解

设 $A=A_{m\times n}$ 秩 $r(A)>0$ ,则有高低分解 $A_{m\times n}=B_{m\times r}C_{r\times n}$ ，其中B为列满秩序(高阵)，C为行满秩(低阵)

性质

$若A=BC,则有 A^H=C^HB^H$

2.5.1 高低分解方法

把 $A=A_{m\times n}$ 做行变换

$\begin{aligned} &A\overset{行变换}{\longrightarrow}\left( \begin{matrix} I_r&*\\ \cdots&\cdots\\ 0&0 \end{matrix} \right)，r(A)=r,I_r=\left( \begin{matrix} 1&&\\&\ddots&\\&&1 \end{matrix} \right)_{r\times r}取出A中前r列，记为\alpha_1,\cdots,\alpha_r\\ &令B=(\alpha_1,\cdots,\alpha_r),C=(I_r,*)，可得A=BC\\ \end{aligned}$

eg：

$\begin{aligned} A=\left( \begin{matrix} 1&1&2\\0&1&1\\1&1&2 \end{matrix} \right)，求高低分解A=BC \end{aligned}$ $\begin{aligned} &A\overset{行变换}{\longrightarrow}\left( \begin{matrix} 1&0&1\\0&1&1\\0&0&0 \end{matrix} \right),令B=(\alpha_1,\alpha_2)=\left( \begin{matrix} 1&1\\0&1\\1&1 \end{matrix} \right),C=\left( \begin{aligned} \begin{matrix} 1&0&1\\0&1&1 \end{matrix} \end{aligned} \right)\\ &得高低分解A=BC=(\alpha_1,\alpha_2)=\left( \begin{matrix} 1&1\\0&1\\1&1 \end{matrix} \right)\left( \begin{aligned} \begin{matrix} 1&0&1\\0&1&1 \end{matrix} \end{aligned} \right) \end{aligned}$

$求A=\left( \begin{matrix} 1&3&2&1&4\\ 2&6&1&0&7\\ 3&9&3&1&11\\ \end{matrix} \right)$ $\begin{aligned} &解1:\\ &A\overset{r_3-r_1-r_2}{\longrightarrow}\left( \begin{matrix} 1&3&2&1&4\\ 2&6&1&0&7\\ 0&0&0&0&0 \end{matrix} \right)\overset{r_2-2r_1}{\longrightarrow}\left( \begin{matrix} 1&3&2&1&4\\ 0&0&-3&-2&-1\\ 0&0&0&0&0 \end{matrix} \right)\overset{r_1+4r_2}{\longrightarrow}\left( \begin{matrix} 1&3&-10&-7&0\\ 0&0&3&2&1\\ 0&0&0&0&0 \end{matrix} \right)\\ &故可取A中第1列和第5列作为高阵B，C=\left( \begin{matrix} 1&3&-10&-7&0\\ 0&0&3&2&1 \end{matrix} \right) \end{aligned}$ $\begin{aligned} &解2:\\ &A\overset{r_3-r_1-r_2}{\longrightarrow}\left( \begin{matrix} 1&3&2&1&4\\ 2&6&1&0&7\\ 0&0&0&0&0 \end{matrix} \right)\overset{r_2-2r_1}{\longrightarrow}\left( \begin{matrix} 1&3&2&1&4\\ 0&0&3&2&1\\ 0&0&0&0&0 \end{matrix} \right)\overset{\frac{1}{3}r_2}{\longrightarrow}\left( \begin{matrix} 1&3&2&1&4\\ 0&0&1&\frac{2}{3}&\frac{1}{3}\\ 0&0&0&0&0 \end{matrix} \right)\\ &\overset{r_1-2r_2}{\longrightarrow}\left( \begin{matrix} 1&3&0&-\frac{1}{3}&\frac{10}{3}\\ 0&0&1&\frac{2}{3}&\frac{1}{3}\\ 0&0&0&0&0 \end{matrix} \right),\\ &取A中的第1,3列为高阵B=\left( \begin{matrix} 1&2\\ 2&1\\ 3&3 \end{matrix} \right),C=\left( \begin{matrix} 1&3&0&-\frac{1}{3}&\frac{10}{3}\\ 0&0&1&\frac{2}{3}&\frac{1}{3}\\ 0&0&0&0&0 \end{matrix} \right) \end{aligned}$

2.5.2 秩1分解法

$若r(A)=1,则A=\left( \begin{matrix} \alpha_1\\\vdots\\\alpha_n \end{matrix} \right)\left(b_1\cdots b_n\right)=\alpha \beta，其中\alpha 为A中的非零列$

eg

$A=\left( \begin{matrix} 1&-1&2&3\\ 2&-2&4&6\\ 1&-1&2&3 \end{matrix} \right)(各列成比例),r(A)=1$ $\begin{aligned} &取\alpha=\left( \begin{matrix} 1\\2\\1 \end{matrix} \right),\beta=\left( 1\quad -1\quad 2\quad 3 \right)\\ &A=BC=\left( \begin{matrix} 1\\2\\1 \end{matrix} \right)\left( 1\quad -1\quad 2\quad 3 \right) \end{aligned}$

$A=\left( \begin{matrix} 1&0&-i&4&2\\ -1&0&i&-4&2\\ -1&0&-i&-3&1+i \end{matrix} \right)$ $\begin{aligned} &A\overset{r_2+r_1,r_3+r_1}{\longrightarrow}\left( \begin{matrix} 1&0&-i&4&2\\ 0&0&0&0&4\\ 0&0&-2i&1&3+i \end{matrix} \right)\overset{\frac{r_2}{4},-\frac{r_3}{2i}}{\longrightarrow}\left( \begin{matrix} 1&0&-i&4&2\\ 0&0&0&0&1\\ 0&0&1&-\frac{1}{2i}&-\frac{3+i}{2i} \end{matrix} \right)\\ &\overset{r_1+ir_3,r_1-r_2,r_3-r_2}{\longrightarrow}\left( \begin{matrix} 1&0&0&\frac{7}{2}&0\\ 0&0&0&0&1\\ 0&0&1&-\frac{1}{2i}&0 \end{matrix} \right),故选第1,3,5列作为高阵B\\ &即B=\left( \begin{matrix} 1&-i&2\\ -1&i&2\\ -1&-i&1+i \end{matrix} \right),C=\left( \begin{matrix} 1&0&0&\frac{7}{2}&0\\ 0&0&0&0&1\\ 0&0&1&-\frac{1}{2i}&0 \end{matrix} \right),A=BC \end{aligned}$

2.5.3 高阵低阵的逆

a. 高阵的左逆

设 $B=B_{m\times r}$ (列无关) 为高阵，则有左逆公式 $B_L=(B^HB)^{-1}B^H$ ，使 $B_LB=I_r$ ,其中 $B_L=B_{r\times m}$

证明：

$\begin{aligned} &先证 B^HB可逆，r(B^HB)=r(B)=r(列向量极大无关组元素)\\ &B^HB为r阶方针，且秩为r，故B^HB一定可逆\Rightarrow (B^HB)^{-1}存在\\ &再证B_LB=(B^HB)^{-1}B^HB=I_r \end{aligned}$

性质：

高阵消去法：
设 $B$ 为高阵，且 $BX=BY$ ，则 $X=Y$
证明：
$\begin{aligned} &令B_L=(B^HB)^{-1}B^H,对于BX=BY，等号两边同时左乘B_L,得B_LBX=B_LBY\\ &I_rX=I_rY\Rightarrow X=Y \end{aligned}$

b. 低阵的右逆

设 $C=C_{r\times n}$ 存在右逆阵，$C_R=C^H(CC^H)^{-1}$ ，使 $CC_R=I_r$

性质：

低阵消去法：
设 $C$ 为低阵，且 $XC=YC$ ，则 $X=Y$