1.准备知识——相似&换位公式&秩1矩阵&内积&正交

矩阵论准备知识，很多内容都是线性代数的扩展

1.1 相似

设 A、B为n阶方阵，如果存在可逆阵P，使得 $P^{-1}AP=B$ ，则称A与B相似，记为 $A\sim B$

1.1.1 相似性质

1. 自反性：$A\sim A$ ，$I^{-1}AI = A$
2. 对称性：$A\sim B \Rightarrow B\Rightarrow A$
3. 传递性：$A\sim B \quad 且 \quad B\sim C\Rightarrow A\sim B$

所以，方阵之间的相似关系是一种等价关系

1.1.2 定理：A与B相似，则有相同特征根公式

若A与B相似，则有

$$\begin{aligned} |xI-A|=|xI-B| \end{aligned}$$

即A与B的特征根公式相同，其中A与B都是n阶方阵

*证明

可设 $P^{-1}AP = B$ ，则有

$$\begin{aligned} \mid xI-B\mid &=\mid xI-P^{-1}AP\mid=\mid P^{-1}(xI-A)P\mid \xlongequal{行列式计算}\mid xI-A\mid \end{aligned}$$

由相似，可将A与B矩阵表示为 $A\sim B$ 或者 $AP=PB$ ，其中P为可逆矩阵

推论

1. n阶方阵 $A_{n\times n}$ 的特征值为 $\lambda(A)=\{\lambda_1,\lambda_2,…,\lambda_n\}$ 可包含重复特征值

   eg

   $$\begin{aligned} &A=\left ( \begin{matrix} 1\quad 1\\ 1\quad 1 \end{matrix} \right),\lambda(A)=\{2,0\}\\\\ &A=\left ( \begin{matrix} 2\quad 1\\ 0\quad 3 \end{matrix} \right),\lambda(A)=\{2,3\}\\\\ &A=\left ( \begin{matrix} 2\quad 1\\ 0\quad 2 \end{matrix} \right),\lambda(A)=\{2,2\} \end{aligned}$$

2. 进而，特征多项式 $\mid \lambda I-A \mid$ 必可分解为 $\mid (\lambda-\lambda_1)(\lambda-\lambda_2)…(\lambda-\lambda_n)\mid$

3. 若 $A\sim B$ ，则特征多项式相同，进而其分解式相等，得出结论，A与B的特征值相同，即 $\lambda(A)=\lambda(B)$

总结：

$相似 \Leftrightarrow 特征多项式相同\Rightarrow 特征值相等$

$特征值相等\xRightarrow{+实对称矩阵} 相似$

特征值是相似变化下的不变量

1.1.3 相似对角化

若 $P^{-1}AP=\Lambda=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)$ ，则 $P$ 中的 $(X_1,X_2,\cdots,X_n)$ 都是A的特征向量，且 $X_1,X_2,\cdots,X_n$ 都是A的特征向量，且 $X_1,\cdots,X_n$ 无关

1.2 换位公式

设问：若 $A=A_{n\times p},B=B_{p\times n}，$且 $p\le n$ ，则 $(A\cdot B)$ 为 n 阶方阵， $(B\cdot A)$ 为 p 阶方阵，求其特征值？

1.2.1 定义

$\vert \lambda I_n-AB \vert= \lambda^{n-p}\vert \lambda I_p-BA \vert$

• $AB$ 为 $n$ 阶方阵， $BA$ 为 $P$ 阶方阵

可见 $AB$ 与 $BA$ 两个方阵特征值基本相等

*证明

1.2.2 推论

若 $A=A_{n\times p},B=B_{p\times n}$ ，且 $p\le n$ ，则 $A\cdot B$ 为 n 阶方阵， $B\cdot A$ 为 p 阶方阵

1. 若 $BA$ 的特征根 $\lambda(BA)=\{\lambda_1,\lambda_2,…,\lambda_p\}$ ，则 $AB$ 的特征根 $\lambda(AB)=\{\lambda_1,\lambda_2…,\lambda_p,0,…,0\}(含n-p个零根)$ ，可见 $AB$ 与 $BA$ 只差 $n-p$ 个零根，其余根相同

   

   即 $AB$ 与 $BA$ 必有相同非零根

   

2. 由于 AB与BA 只相差 $n-p$ 个零根，所以 $tr(AB) = tr(BA)$

   证：$tr(AB)=\lambda_1+\lambda_2+\cdots+\lambda_p+0+\cdots+0=tr(BA)$

3. $\mid I_n \pm AB\mid = \mid I_p\pm BA\mid$ ，当 $\lambda = 1,A取-A$ 时，分别可证

4. 若 n>p，则 $\mid AB \mid=0$

   证明：

   $AB$ 为 $n$ 阶矩阵，由于 $r(AB)\le r(A)\le p<n(矩阵的秩越乘越小)$ ，故 $\mid AB\mid=0$

   或者考虑 $AB$ 为 $n$ 阶方阵，必有 $n-p$ 个零特征值，$\mid AB \mid = \prod\lambda_i = 0$

   

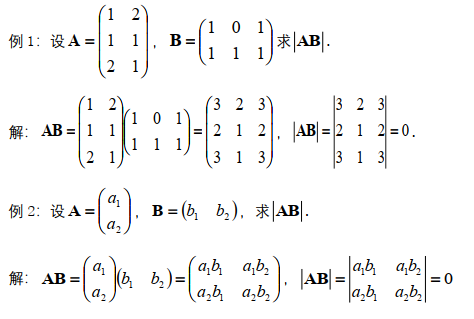
   例3：$P = \left(\begin{matrix}I&A \\0&I\end{matrix}\right)$ ，求证 $P^{-1}=\left(\begin{matrix}I&-A\\0& I\end{matrix}\right)$ （其实也就是二阶矩阵求逆）

   $$\begin{aligned} A=\left( \begin{matrix} B\quad C\\ D\quad E \end{matrix} \right),则A^{-1}=\frac{1}{\vert A\vert}\left( \begin{matrix} E\quad -C\\ -D\quad B \end{matrix} \right) \end{aligned}$$

1.3 秩1矩阵

$$\begin{aligned} A&=\left( \begin{matrix} a_1b_1\quad &a_1b_2\quad &\cdots\quad &a_1b_n\\ a_2b_1\quad &a_2b_2\quad &\cdots\quad &a_2b_n\\ \vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ a_nb_1\quad &a_nb_2\quad &\cdots\quad &a_nb_n \end{matrix} \right)_{n\times n}=\left( \begin{matrix} a_1\\a_2\\\vdots \\a_n \end{matrix} \right)\left( b_1\quad b_2\quad \cdots \quad b_n \right)\overset{\Delta}{=}\alpha \beta^{T}\\\\ &其中 \alpha=\left( \begin{matrix} a_1\\a_2\\\vdots \\a_n \end{matrix} \right),\beta=\left( \begin{matrix} b_1\\b_2\\\vdots \\b_n \end{matrix} \right) \end{aligned}$$

1.3.1 秩1矩阵特征方程

$$\begin{aligned} &\mid \lambda I_n-A\mid = \mid \lambda I_n-\alpha_{n\times 1}\beta_{1\times n}^T\mid\xlongequal{换位公式:\vert\lambda_n-(AB)_n \vert=\lambda^{n-p}\vert \lambda I_p-(BA)_p\vert}\lambda^{n-1}\mid\lambda I_1-\beta_{1\times n}^T\alpha_{n\times 1}I_1\mid\\ &=\lambda^{n-1}(\lambda I-tr(A)),其中 tr(A)=\sum\limits_{i=1}\limits^{n}a_{ii}b_{ii} \end{aligned}$$

eg

1.3.3 秩1矩阵的特征值

若 $A = A_{n\times n}$ ，$r(A)=1$ ，则全体特征值为 $\lambda(A)=\{tr(A),0,…,0\}$ ，其中 $tr(A)=a_1b_1+a_2b_2+…+a_nb_n=\beta^T\alpha$

证明：

由换位公式可知，$\alpha_{n\times 1}\beta_{1\times n}^T$ 与 $\beta_{1\times n}^T\alpha_{n\times 1}$ 相差 n-1 个零根，即有一个相等的非零特征根，而 $\beta_{1\times n}^T\alpha_{n\times 1}$ 为1阶矩阵，所以 $\lambda_1=\beta_{1\times n}^T\alpha_{n\times 1}=a_1b_1+a_2b_2+…+a_nb_n=tr(A)$

1.3.4 秩1矩阵特征向量

$A=\alpha \beta^T$ 的列向量都是 $\lambda_1=tr(A)$ 的特征向量

证明：

$$\begin{aligned} A\alpha = (\alpha \beta)\alpha=\lambda_1 \alpha \end{aligned}$$

eg

$$\begin{aligned} &A为秩1矩阵，\lambda(A)=\{tr(A),0,0\}=\{-2,0,0\}\\ &可知 \vert \lambda I-A\vert=x^2(x+2),其中\lambda_1=-2,可取\left(\begin{matrix}1\\1\\2\end{matrix}\right)为A的特向，A\left(\begin{matrix}1\\1\\2\end{matrix}\right)=-2\left(\begin{matrix}1\\1\\2\end{matrix}\right) \end{aligned}$$

---

$$\begin{aligned} &A为秩1矩阵，全体特根\lambda(A)=\{tr(A),0,0\}=\{9,0,0\},可知 \vert \lambda I-A\vert=\lambda^2(\lambda-9)\\ &\lambda_1=9,可知A的列向量\left(\begin{matrix}1\\1\\-1\end{matrix}\right)为一个特向，A\left(\begin{matrix}1\\1\\-1\end{matrix}\right)=9\left(\begin{matrix}1\\1\\-1\end{matrix}\right) \end{aligned}$$

1.4 平移矩阵

$A+cI$ 称为A的平移矩阵

1.4.1 平移法

a. 特征值

若 $\lambda(A)=\{\lambda_1+c,\lambda_2+c,…,\lambda_n+c\}$

b. 特征向量

$A+cI$ 与 $A$ 有相同的特征向量

证明：

$$\begin{aligned} &令A的n个特征向量x_1,x_2,...,x_n，有\\\\ &Ax_1=\lambda_1 x_1,Ax_1=\lambda_2 x_2,...Ax_n=\lambda_1 x_n\\\\ \Leftrightarrow & \left\{ \begin{aligned} (A+cI)x_1 = \lambda_1x_1+cx_1=(\lambda_1+c)x_1\\ (A+cI)x_2 = \lambda_2x_2+cx_2=(\lambda_2+c)x_2\\ \cdots\\ (A+cI)x_n = \lambda_nx_n+cx_n=(\lambda_n+c)x_n \end{aligned} \right.\\\\ 故&\lambda(A)=\{\lambda_1,\lambda_2,...,\lambda_n\} \end{aligned}$$

eg：平移法求特征向量

$$\begin{aligned} &(1)A-E=\left( \begin{matrix} 0\quad 1\quad 0\\ 0\quad 1\quad 0\\ 0\quad 1\quad 0 \end{matrix} \right)\\ &由秩1公式,\lambda(A-E)=\{tr(A),0,0\},\\ &由平移公式 \lambda(A)=\{tr(A-E)+1,1,1\}=\{2,1,1\}\\ &且(A-E)与A的特征向量相等，A-E的列向量\left( \begin{matrix} 1\\1\\1 \end{matrix} \right)\\ &(2)A-E=\left( \begin{matrix} 3& 6 & 0\\ -3& -6& 0\\ -3& -6& 0\\ \end{matrix} \right),\lambda(A-E)=\{-3,0,0\}, \\&故\lambda(A)=\{-2,1,1\},A的特征向量为\left( \begin{matrix} 3\\-3\\6 \end{matrix} \right) \end{aligned}$$

---

$$\begin{aligned} &A=\left( \begin{matrix} -1& -2& 6\\ -1& 0& 3\\ -1& -1& 4 \end{matrix} \right)，A-I=\left( \begin{matrix} -2& -2& 6\\ -1& -1& 3\\ -1& -1& 3 \end{matrix} \right),\lambda(A-I)=\{0,0,0\}\\ &,则\lambda(A)=\lambda(A-I)+1=\{1,1,1\} \end{aligned}$$

---

$$\begin{aligned} &A=\left( \begin{matrix} 7& 4& -1\\ 4& 7& -1\\ -4& -4& 4 \end{matrix} \right),A-3I=\left( \begin{matrix} 4& 4& -1\\ 4& 4& -1\\ -4& -4& 1 \end{matrix} \right),\lambda(A-3I)=\{9,0,0\}\\ \\&\lambda(A)=\lambda(A-3I)+3=\{12,3,3\} \end{aligned}$$

1.4.2 倍法

若 $\lambda(A)=\{\lambda_1,…,\lambda_n\}$ ，则 $\lambda(kA)=\{k\lambda_1,k\lambda_2,…,k\lambda_n,\}(k\neq 0)$

$kA$ 与 $A$ 有相同的特征向量

1.5 复数域

1.5.1 复数

$C:\{z=a+bi\mid a,b\in R\}$ ，其中 $i^2=-1,\sqrt{-1}=i$

• $R\subset C$ ：实数都是复数

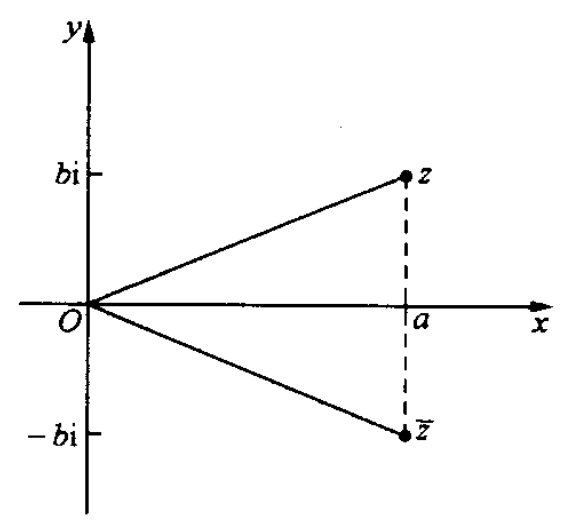
$若z=a+bi,则\overline{z}=\overline{a+bi}=a-bi$

a. 复数域表示

$n$ 维实列向量, $X=\left(\begin{matrix}x_1\\ x_2 \\ \vdots \\x_n\end{matrix}\right),x_i\in R$ ，$n$ 维实复列向量 $X=\left(\begin{matrix}x_1\\ x_2 \\ \vdots \\x_n\end{matrix}\right),x_i\in C$ ，列向量可表示为转置形式 $X=\left(x_1,x_2,…,x_n\right)^T,X\in C^n$ ，实矩阵 $R_{m\times n} = \{A=(a_{ij})\mid a_{i,j}\in R,1\le i\le m,1\le j\le n\}$ ，复矩阵 $C^{m\times n}=\{A=(a_{ij})\mid a_{ij}\in C,1\le i\le m,1\le j\le n\}$ ，且 $R_{m\times n}\in C^{m\times n}$ ，$A_{m\times n}=\left(\begin{matrix}a_{11}\quad &a_{12}&\cdots\quad &a_{1n}\\a_{21}\quad &a_{22}&\cdots\quad &a_{2n}\\ \vdots\quad &\vdots &\ddots\quad &\vdots\\a_{m1}\quad &a_{m2}&\cdots \quad &a_{mn}\end{matrix}\right)\in C^{m\times n}$ ，可表示为 $A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ ，且 $\alpha_i\in C^{m}$

b. 复数性质

1. $\mid z \mid = \mid\overline z \mid$
2. $\mid kz \mid=k\mid z\mid,k\in C$
3. $\mid z_1+z_2 \mid \le \mid z_1 \mid+\mid z_2 \mid$
4. $\overline{z_1\cdot z_2}=\overline{z_1} \cdot \overline{z_2}$

1.5.2 共轭公式

由 $z\overline{z}=(a+bi)(a-bi)=a^2+b^2$

• 规定 $\mid z \mid=\sqrt{a^2+b^2}$ 为z的模长

模公式 $z\overline z=\overline zz=\mid z\mid^2=a^2+b^2$

复矩阵的共轭

$A=(a_{ij})=\left(\begin{matrix}a_{11}&\cdots &a_{1n}\\\vdots &\ddots &\vdots\\a_{n1}&\cdots &a_{nn}\\\end{matrix}\right)$ ，$A$ 的共轭矩阵 $\overline{A}=(\overline{a_{ij}})=\left(\begin{matrix}\overline{a_{11}}&\cdots &\overline{a_{1n}}\\\vdots&\ddots &\vdots\\\overline{a_{n1}}&\cdots &\overline{a_{nn}}\\\end{matrix}\right)$

eg：

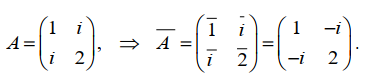
乘后共轭=共轭后乘 ： $\overline{A\cdot B}=\overline{A}\cdot \overline{B}$

1.5.3 Hermite变换

共轭转置记为 Hermite 变换，即 $A^H = \overline{A}^T=\overline{A^T}$

$$\begin{aligned} &A=(a_{ij})=\left( \begin{matrix} a_{11}&\cdots &a_{1n}\\ \cdots &\ddots &\cdots\\ a_{m1}&\cdots & a^{mn} \end{matrix} \right)\in C^{m\times n},\\ &\overline{A}=\left( \begin{matrix} \overline{a_{11}}&\cdots &\overline{a_{1n}}\\ \vdots &\ddots &\vdots\\ \overline{a_{m1}}&\cdots &\overline{a_{mn}} \end{matrix} \right)\in C^{m\times n}\\ &X=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right)\in C^n,则X^H=(\overline{x_1},\overline{x_2},...,\overline{x_n}) \end{aligned}$$

共轭不会使矩阵变型，转置使矩阵变型 $A\in C^{n\times p}\Rightarrow A^H\in C^{p\times n}$

eg：

$$\begin{aligned} A=\left( \begin{matrix} 1\quad i\\ 1\quad i\\ 1\quad i \end{matrix} \right)\in C^{3\times2},则A^H=\left( \begin{matrix} 1\quad -i\\ 1\quad -i\\ 1\quad -i \end{matrix} \right)^T =\left( \begin{matrix} 1\quad 1\quad 1\\ -i\quad -i\quad -i \end{matrix} \right) \in C^{2\times 3} \end{aligned}$$

a. Hermite变换性质

Hermite变换	转置
$(A^H)^H=A$	$(A^T)^T=A$
$(kA)^H=\overline{k}A^H$	$(kA)^T=kA^T$
$(A+B)^H=A^H+B^H$	$(A+B)^T=A^T+B^T$
$(AB)^H=B^HA^H,(ABC)^H=C^HB^HA^H$	$(AB)^T=B^TA^T$

实数阵的 Hermite 变换仍是其本身

• $a\in C 是实数 \iff \overline{a}=a\iff a^H=a$

b. Hermite变换相关的矩阵分类

Hermite变换	转置
$A^H=A$ Hermite矩阵	$A^T=A$ ，对称阵
$A^H=-A$ 斜Hermite矩阵	$A^T=-A$ ，反对称阵

1.6 内积

$X=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right),Y=\left(\begin{matrix}y_1\\y_2\\\vdots\\y_n\end{matrix}\right)\in C^n$

1.6.1 复向量内积

$(X,Y)\overset{\Delta}{=}Y^HX=x_1\overline{y_1}+x_2\overline{y_2}+\cdots+x_n\overline{y_n}=\sum\limits_{i=1}\limits^{n}x_i\overline{y_i}=tr(Y^HX)$

$(Y,X)=X^HY=\overline{x_1}y_1+\overline{x_2}y_2+\cdots+\overline{x_n}y_1=\sum\limits_{i=1}\limits^{n}\overline{x_i}y_i=tr(X^HY)$

若取 $Y=X$ ，则其内积

$$\begin{aligned} (X,X)&=X^HX=x_1\overline{x_1}+x_2\overline{x_2}+\cdots+x_n\overline{x_n}=\sum\limits_{i=1}\limits^{n}x_i\overline{x_i}\\ &=\vert x_1 \vert^2+\vert x_2 \vert^2+\cdots+\vert x_n \vert^2 = \vert X \vert^2\\ &=tr(X^HX)=tr(XX^H) \end{aligned}$$

向量内积性质

1. $(X,X)\ge 0$ ；若 $X\neq 0 ,(X,X)> 0$

2. $(X,Y)=\overline{(Y,X)}$

3. $(kX,Y)=k(X,Y),(X,kY)=\overline{k}(X,Y)$

4. $(X+Y,W)=(X,W)+(Y,W)$

   $(X,Y+W)=(X,Y)+(X,W)$

5. $\vert (X,Y) \vert^2\le \vert X \vert\cdot\vert Y \vert$

1.6.2 复矩阵内积

a. 定义

$$\begin{aligned} &(A,B)\overset{\Delta}{=}tr(B^HA)=tr(A^HB)=\sum a_{ij}\overline{b_{ij}},A,B\in C^{m,n}\\ &(A,A)\xlongequal{\Delta}tr(A^HA)=tr(AA^H)=\sum a_{ij}\overline{a_{ij}}=\sum \vert a_{ij} \vert^2 \end{aligned}$$

矩阵A的模长：$\vert \vert A \vert \vert=\sqrt{(A,A)}=\sqrt{tr(AA^H)}=\sqrt{\sum\vert a_{ij} \vert^2}$

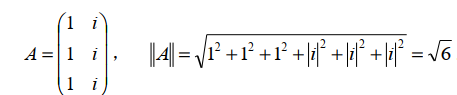
b. 性质

1. $(A,A)=tr(A^HA)=\sum\vert a_{ij} \vert^2 \ge 0$ ；若 $A\neq 0$ ，则 $(A,A)>0$

2. $(A,B)=\overline{(B,A)}$

3. $(kA,B)=k(A,B),(A,kB)=\overline{k}(A,B)$

4. (A+B,D)=(A,D)+(B,D)，(D,A+B)=(D,A)+(D,B)

5. $\vert (A,B) \vert^2 \le \vert A\vert\cdot\vert B \vert$

c. 矩阵的内积形式

列分块（常用）

$$\begin{aligned} A&=\left( \begin{matrix} a_{11}\quad&\cdots&a_{1p}\\ \vdots\quad&\ddots&\vdots\\ a_{n1}\quad&\cdots&a_{np} \end{matrix} \right)\in C^{n\times p}\\ &=(\alpha_1,\cdots,\alpha_p),其中\alpha_i为n维列向量(n\times 1阶矩阵)\\\\ A^H&=\left( \begin{matrix} \overline{a_{11}}\quad&\cdots\quad &\overline{a_{n1}}\\ \vdots\quad &\ddots&\vdots\\ \overline{a_{1p}}\quad&\cdots\quad &\overline{a_{np}}\\ \end{matrix} \right)\in C^{p\times n}\\ &=\left( \begin{matrix} \overline{\alpha_1}^T\\ \vdots\\ \overline{\alpha_p}^T \end{matrix} \right)，其中\overline{\alpha_1}^T是n维行向量(1\times n阶矩阵)\\\\ \end{aligned}$$ $$\begin{aligned} A^HA&=\left( \begin{matrix} \overline{\alpha_1}^T\\ \vdots\\ \overline{\alpha_p}^T \end{matrix} \right)(\alpha_1,\cdots,\alpha_p)\\\\ &=\left( \begin{matrix} \overline{\alpha_1}^T\alpha_1\quad&\overline{\alpha_1}^T\alpha_2\quad &\cdots&\overline{\alpha_1}^T\alpha_p\\ \overline{\alpha_2}^T\alpha_1\quad&\overline{\alpha_2}^T\alpha_2\quad &\cdots&\overline{\alpha_2}^T\alpha_p\\ \vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ \overline{\alpha_p}^T\alpha_1\quad&\overline{\alpha_p}^T\alpha_2\quad &\cdots&\overline{\alpha_p}^T\alpha_p \end{matrix} \right)\\\\ &=\left( \begin{matrix} (\alpha_1,\alpha_1)\quad &(\alpha_2,\alpha_1)\quad&\cdots\quad &(\alpha_p,\alpha_1)\\ (\alpha_1,\alpha_2)\quad &(\alpha_2,\alpha_2)\quad&\cdots\quad &(\alpha_p,\alpha_2)\\ \vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ (\alpha_1,\alpha_p)\quad &(\alpha_2,\alpha_p)\quad&\cdots\quad &(\alpha_p,\alpha_p) \end{matrix} \right)\\\\ &=\left( \begin{matrix} \overline{(\alpha_1,\alpha_1)}\quad &\overline{(\alpha_1,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_1,\alpha_p)}\\ \overline{(\alpha_2,\alpha_1)}\quad &\overline{(\alpha_2,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_2,\alpha_p)}\\ \vdots\quad&\vdots\quad &\ddots\quad &\vdots\\ \overline{(\alpha_p,\alpha_1)}\quad &\overline{(\alpha_p,\alpha_2)}\quad&\cdots\quad &\overline{(\alpha_p,\alpha_p)} \end{matrix} \right)\\ \end{aligned}$$

行分块

$$\begin{aligned} A&=\left( \begin{matrix} a_{11}\quad&\cdots&a_{1p}\\ \vdots\quad&\ddots&\vdots\\ a_{n1}\quad&\cdots&a_{np} \end{matrix} \right)\in C^{n\times p}\\ &=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right),其中\alpha_i为p维行向量(1\times p阶矩阵)\\\\ A^H&=\left( \begin{matrix} \overline{\alpha_1}^T\quad \overline{\alpha_2}^T\quad \cdots\quad \overline{\alpha_n}^T \end{matrix} \right),其中\overline{\alpha_i}^T 为p维列向量(p\times 1阶矩阵) \end{aligned}$$ $$\begin{aligned} AA^H&=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \vdots\\ \alpha_n \end{matrix} \right)\left( \begin{matrix} \overline{\alpha_1}^T\quad \overline{\alpha_2}^T\quad \cdots\quad \overline{\alpha_n}^T \end{matrix} \right)\\\\ &=\left( \begin{matrix} \alpha_1\overline{\alpha_1}^T\quad &\alpha_1\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_1\overline{\alpha_n}^T\\ \alpha_2\overline{\alpha_1}^T\quad &\alpha_2\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_2\overline{\alpha_n}^T\\ \vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ \alpha_n\overline{\alpha_1}^T &\quad\alpha_n\overline{\alpha_2}^T\quad&\cdots\quad &\alpha_n\overline{\alpha_n}^T \end{matrix} \right)\\\\ &=\left( \begin{matrix} (\alpha_1,\alpha_1)\quad &(\alpha_1,\alpha_2)\quad &\cdots\quad &(\alpha_1,\alpha_n)\\ (\alpha_2,\alpha_1)\quad &(\alpha_2,\alpha_2)\quad &\cdots\quad &(\alpha_2,\alpha_n)\\ \vdots\quad &\vdots\quad &\ddots\quad &\vdots\\ (\alpha_n,\alpha_1)\quad &(\alpha_n,\alpha_2)\quad &\cdots\quad &(\alpha_n,\alpha_n) \end{matrix} \right) \end{aligned}$$

1.6.3 模长

a. 复向量模长

列向量模长

$$\begin{aligned} &X=\left( \begin{matrix} x_1\\x_2\\\vdots\\x_n \end{matrix} \right)\in C,则其模长 \mid X \mid = \sqrt{ \mid x_1 \mid^2+ \mid x_2 \mid^2+ \cdots \mid x_n \mid^2} \end{aligned}$$

模长性质

$\mid k\cdot X \mid = \mid k \mid \cdot \mid X \mid ,k\in C$

$\vert \frac{X}{k} \vert=\frac{\vert X\vert}{\vert k \vert},(k\neq \vec{0})$

$\vert X\pm Y\vert \le \vert X\vert + \vert Y \vert$

模平方公式

$$\begin{aligned} &令X=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right)\in C,则 \left\{ \begin{aligned} &① X^HX=\mid X \mid^2\\\\ &②tr(X^HX)=tr(XX^H)=\mid X \mid^2 \end{aligned} \right.,其中\\ &\mid X \mid^2 = \mid x_1 \mid ^2 + \mid x_2 \mid^2+\cdots+\mid x_n \mid^2=\sum\limits_{i=1}\limits^{n}\mid x_i \mid^2 \end{aligned}$$

区分 ：复数的模平方和复数平方的模

• 复数的模平方 $\mid x_1 \mid^2=(a+bi)(a-bi)=a^2+b^2 \ge 0$
• 复数平方的模：$\mid x_1^2 \mid=(a+bi)^2= a^2-b^2+2abi$

eg

$$\begin{aligned} &X=\left( \begin{matrix} 1\\i\\1 \end{matrix} \right)\in C^3,XX^H=\left( \begin{matrix} 1\\i\\1 \end{matrix} \right)(1\quad -i\quad 1)=\left( \begin{matrix} &1\quad &\quad &*\\ &\quad &1&\quad\\ &*&\quad&1 \end{matrix} \right)\\ &\therefore tr(X^HX)=tr(XX^H)=\vert 1 \vert^2+\vert -i^2 \vert^2+\vert 1 \vert^2 = 3 \end{aligned}$$

b. 复矩阵模长

$$\begin{aligned} &令A=(a_{ij})\in C,则模长(矩阵的F范数)\mid \mid A \mid\mid=\sqrt{\sum\limits_{i=1}\limits^{n}\mid a_{ij} \mid^2} \end{aligned}$$

复矩阵的模平方公式

$$\begin{aligned} &设A=(a_{ij})_{n\times p},则 \quad tr(A^HA)=tr(AA^H)=\mid\mid A\mid\mid^2 = \sum\limits_{i=1}\limits^{n}\mid a_{ij} \mid^2 \end{aligned}$$

eg

$$\begin{aligned} X=\left( \begin{matrix} 1\\i\\1 \end{matrix} \right)\in C^{3\times 1},则\mid X \mid^2 = X^HX=(1,-i,1)\left( \begin{matrix} 1\\i\\1 \end{matrix} \right)=1+-i^2+1=3 \end{aligned}$$

对于方阵 $A=(a_{ij})_{n\times n}$ ，有

$$\begin{aligned} \left\{ \begin{aligned} &tr(A)\overset{\Delta}{=} a_{11}+a_{22}+\cdots+a_{nn}=\sum\limits_{i=1}\limits^{n}\lambda_i\\ &det(A) = \mid A \mid = \prod\limits_{i=1}\limits^{n}\lambda_i \end{aligned} \right. \end{aligned}$$

1.7 正交

1.7.1 向量正交

$$\begin{aligned} X&=\left( \begin{matrix} x_1\\ x_2\\ \vdots\\ x_n \end{matrix} \right),Y=\left( \begin{matrix} y_1\\ y_2\\ \vdots\\ y_n \end{matrix} \right)\in C^{n} \end{aligned}$$ $$\begin{aligned} X\bot Y\iff (X,Y)=0&=x_1\overline{y_1}+x_2\overline{y_2}+\cdots+x_n\overline{y_n}\\\\ &=\overline{\overline{x_1}y_1+\overline{x_2}y_2+\cdots+\overline{x_n}y_n}\\ =(Y,X) \end{aligned}$$

正交性质

1. $X\bot Y\Rightarrow aX\bot bY$

   证：$(aX,bY)=\overline{b}Y^HaX=a\overline{b}Y^HX=a\overline{b}(X,Y)=0$

2. 勾股定理：$X_1\bot X_2\bot \cdots \pm X_n\Rightarrow \vert c_1X_1\pm c_2X_2\bot \cdots \pm c_nX_n\vert^2=\vert c_1X_1\vert^2+\vert c_2X_2\vert^2+\cdots+\vert c_nX_n\vert^2$

   此时，$X_1,X_2,\cdots,x_n$ 称为一个正交组

1.7.2 单位向量

若 $X\neq \vec{0}$ ，$\frac{X}{\vert X \vert}$ 是一个单位向量（$\vert \frac{X}{\vert X \vert} \vert=1$）

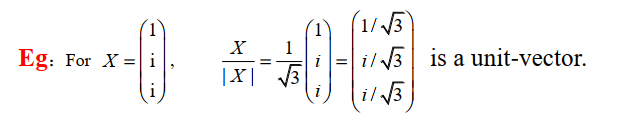
1.7.3 优阵(正交阵)

预：非单位列向量

半：p个n维列向量(p<n)

a. 预-半优阵(预-半正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_p$ 是 $n$ 维列向量，且 $p\le n$ ，且 $\alpha_1\bot\alpha_2\bot \cdots\bot\alpha_p$
，则称 $A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 为预半优阵

判定

$A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 是预半优阵 $\iff A^HA=\left(\begin{matrix}(\alpha_1,\alpha_1)&\cdots&0\\\vdots&\ddots&0\\0&\cdots&(\alpha_p,\alpha_p)\end{matrix}\right)$ 是对角阵，其中 $\alpha_1,\alpha_2,\cdots,\alpha_p$ 是 $n$ 维列向量

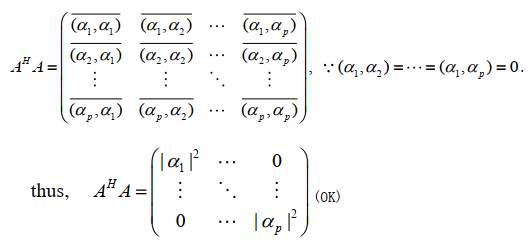
区分 ： $A^HA$ 是 $p \times p$ 阶满秩方阵，而 $AA^H$ 是 $n\times n$ 不满秩方阵

b. 半优阵(半正交阵)

$A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 是预半优阵，其中 $\alpha_i$ 是 $n$ 维列向量，若满足 $\vert \alpha_1 \vert=\vert \alpha_2 \vert=\cdots=\vert \alpha_p \vert = 1$ ，则A为半优阵

判定

$A=(\alpha_1,\cdots,\alpha_p)$ 是半优阵 $\iff \alpha_1\bot\cdots\bot\alpha_p$ ，且 $\vert \alpha_1 \vert=\cdots=\vert \alpha_p \vert=1$ $\iff A^HA=I_{p}$

性质

1. 保模长 A为半U阵，则 $\vert Ax \vert^2=\vert x \vert^2$

   $\vert Ax \vert^2=(Ax)^H(Ax)=x^HA^HAx=\vert X\vert^2$

2. 保正交 A为半优阵，$x\bot y$ ，则$Ax\bot Ay$

c. 预-优阵(预-单位正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_n$ 是 $n$ 维列向量，且 $\alpha_1\bot\alpha_2\bot\cdots\bot\alpha_n$ ，则 $A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ 是预优阵

eg

$$\begin{aligned} &X_1=\left( \begin{matrix} 1\\i\\i \end{matrix} \right),X_2=\left( \begin{matrix} 2i\\1\\1 \end{matrix} \right),X_3=\left( \begin{matrix} 0\\1\\-1 \end{matrix} \right)\\\\ &(X_1,X_2)=0,(X_2,X_3)=0,(X_1,X_3)=0,\\\\ &\therefore X_1\bot X_2\bot X_3,A=(X_1,X_2,X_3)是预-优阵 \end{aligned}$$

判定

$$\begin{aligned} A&=(\alpha_1,\alpha_2,\cdots,\alpha_n)\\ &\iff A^HA=\left( \begin{matrix} &(\alpha_1,\alpha_1)&\cdots&0\\ &\vdots&\ddots&0\\ &0&\cdots&(\alpha_n,\alpha_n) \end{matrix} \right)是对角阵\\ &其中，\alpha_1,\alpha_2,\cdots,\alpha_p是n维列向量 \end{aligned}$$

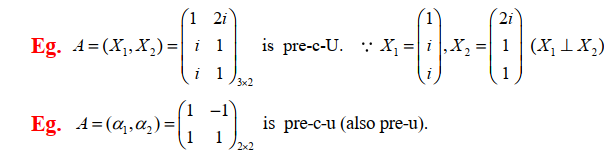
d. 优阵(正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_n$ 是 $n$ 维列向量，$\alpha_1\bot\alpha_2\bot\cdots\bot\alpha_n$ 且 $\vert \alpha_1 \vert=\cdots=\vert \alpha_n \vert=1$ ，则 $A$ 是一个优阵(正交阵)

性质

• $A=A_{n\times n}$ 为优阵($A^HA=I$)，即 $A$ 的列向量 $\alpha_1,\alpha_2,\cdots,\alpha_n$ 为单位正交向量组
• $A^{-1}=A^H$
• $A^HA=I,且AA^H=I$

判定

1. $A$ 是优阵 $\iff A^HA=I\iff A^{-1}A=I\iff AA^H=I$ $\iff A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ ，且 $\alpha_1\bot\alpha_2,\cdots\bot\alpha_n$ ，$\vert \alpha_1\vert=\cdots=\vert\alpha_n\vert=1$

2. $\vert Ax\vert^2=\vert x \vert^2$ ，$A$ 是优阵

   $$\because \vert Ax\vert^2 = (Ax)^H(Ax)=x^HA^HAx=x^HIx=(x,x)=\vert x \vert^2$$

3. $x\bot y \Rightarrow Ax\bot Ay$ ，$A$ 是优阵

   $$\because (Ax,Ay)=(Ay)^HAx=y^HA^HAx=(x,y)=0\iff Ax\bot Ay$$

4. $(Ax,Ay)=(x,y)$，$A$ 是优阵

优阵构造

预优阵到优阵

$$\begin{aligned} A=(\alpha_1,\cdots,\alpha_n) 是预优阵\Rightarrow A=(\frac{\alpha_1}{\vert \alpha_1\vert},\frac{\alpha_2}{\vert \alpha_2\vert},\cdots,\frac{\alpha_n}{\vert \alpha_n \vert})是优阵 \end{aligned}$$

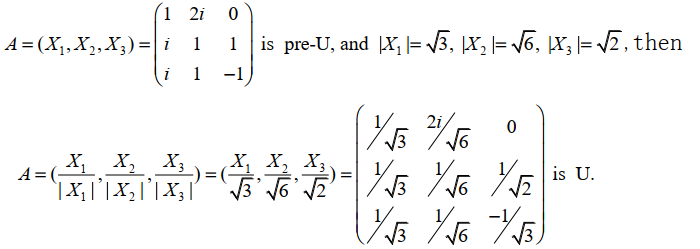
优阵到优阵

若 $A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ 为优阵，则

1. $k=\pm1,kA=(k\alpha_1,k\alpha_2,\cdots,k\alpha_n)$ 为优阵
2. $B=(\beta_1,\beta_2,\cdots,\beta_n)$ 为优阵，其中 $\beta$ 组为 $\alpha$ 组的重排
3. (封闭性)若 $A$、$B$ 为同阶优阵，则 $AB$ 也为优阵

向量构造优阵

将向量作为镜面阵的法向量，构造镜面阵（优阵+H阵）

若 $\alpha=\left(\begin{matrix}a_1\\a_2\\\vdots \\ a_n\end{matrix}\right)\in C$ ，$A=I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2}$ 是一个优阵

1. $A^H=A$ 且 $A^2=I(A^{-1}=A)$

2. $A$ 为优阵 $(A^HA=I)$

   $$\begin{aligned} 1.A^2&=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})\\ &=I_n^2-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4(\alpha\alpha^H)(\alpha\alpha^H)}{\vert \alpha\vert^4}=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha(\alpha^H\alpha)\alpha^H}{\vert \alpha\vert^4} \\ &=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha(\vert \alpha\vert^2)\alpha^H}{\vert \alpha\vert^4}=I_n-\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}+\frac{4\alpha\alpha^H}{\vert \alpha \vert^2}=I_n\\ 2.A^HA&=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})^H(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})\\ &=(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})(I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2})=A^2=I\\ &\therefore A是U阵 \end{aligned}$$

eg ：

$$\begin{aligned} \alpha=\left( \begin{matrix} 1\\1\\1 \end{matrix} \right),其U阵为 I_3-\frac{2\alpha\alpha^H}{\vert \alpha\vert^2}&=\left( \begin{matrix} 1&0&0\\0&1&0\\0&0&1\\ \end{matrix} \right)-\frac{2}{3}\left( \begin{matrix} 1&1&1\\1&1&1\\1&1&1\\ \end{matrix} \right)\\ &=\left( \begin{matrix} \frac{1}{3}&-\frac{2}{3}&-\frac{2}{3}\\ -\frac{2}{3}&\frac{1}{3}&-\frac{2}{3}\\ -\frac{2}{3}&-\frac{2}{3}&\frac{1}{3}\\ \end{matrix} \right) \end{aligned}$$

1.8 特殊矩阵的乘积

1.8.1 对角阵的乘积

$$\begin{aligned} &\Lambda=\left( \begin{matrix} \lambda_1 &\quad&\quad&\quad\\ \quad &\lambda_2 &\quad&\quad\\ \quad &\quad &\ddots&\quad\\ \quad &\quad &\quad&\lambda_n\\ \end{matrix} \right)\\ &\Lambda^H\Lambda=\left( \begin{matrix} \overline{\lambda_1}\lambda_1&\quad&\quad&\quad\\ &\overline{\lambda_2}\lambda_2 &\quad&\quad\\ &&\ddots&\quad\\ &&&\overline{\lambda_n}\lambda_n\\ \end{matrix} \right) =\left( \begin{matrix} \vert \lambda_1\vert^2 &\quad&\quad&\quad\\ &\vert \lambda_2\vert^2 &\quad&\quad\\ &&\ddots&\quad\\ &&&\vert \lambda_n\vert^2\\ \end{matrix} \right) \end{aligned}$$

1.8.2 上三角阵的乘积

1.9 特商公式

$$\begin{aligned} &\lambda_1=\frac{X^HAX}{\vert X\vert^2},其中(X\neq 0为\lambda_1的一个特征向量)\\\\ &证明:X^HAX=X^H\lambda X=\lambda X^HX=\lambda \vert X\vert^2(\vert X\vert^2>0) \end{aligned}$$

1.10 许尔公式(上三角)

1.10.1 Xhur 1-1

任一方阵，$A\in C^{n\times n}$ ，必存在可逆阵 $P$ ，使 $P^{-1}AP=B$ ，$B=\left(\begin{matrix}\lambda_1&&\cdots&\\0&\lambda_2&\cdots&*\\\vdots&\vdots &\ddots&\vdots\\0&0 &\cdots&\lambda_n\\\end{matrix}\right)$ 为上三角阵

若当型

由Xhur公式1-1，一定 $\exists$ 更好的可逆阵 $P$ ，使得 $P^{-1}AP=B=\left(\begin{matrix}\lambda_1&&&\\&\lambda_2&&\\&&\ddots&\\&&&\lambda_n\end{matrix}\right)$ ，其中 $$ 为 $0或1$ ，也称为双线上三角

1.10.2 Xhur 1-2

任一方阵，$A\in C^{n\times n}$ ，必存在优阵 $Q$ ，使 $Q^{-1}AQ=Q^HAQ=B$ ，$B=\left(\begin{matrix}\lambda_1&&\cdots&\\0&\lambda_2&\cdots&*\\\vdots&\vdots &\ddots&\vdots\\0&0 &\cdots&\lambda_n\\\end{matrix}\right)$ 为上三角阵

• 每个矩阵都优相似于上三角阵

1.11 H阵

定义：$A^H=A$ ，则矩阵为 $A$

1.11.1 性质

a. 对角线上元素都是实数

证明：

$A=\left(\begin{matrix}a_{11}&\quad&\quad &\\\quad&a_{22}&\quad&\quad \\\quad &\quad&\ddots&\quad\\&\quad&\quad&a_{nn}\end{matrix}\right)$ ，而 $A^H=\left(\begin{matrix}\overline{a_{11}}&\quad&\quad &\\\quad&\overline{a_{22}}&\quad&\quad \\\quad &\quad&\ddots&\quad\\&\quad&\quad&\overline{a_{nn}}\end{matrix}\right)$ ，由Hermite性质，$A^H=A$ ，则 $a_{11}=\overline{a_{11}},a_{22}=\overline{a_{22}},…,a_{nn}=\overline{a_{nn}}$ ，可见 Hermite阵对角线元素为实数

b. 特根

若 $A^H=A$ 是Hermite矩阵，则特征根都是实数，$\{\lambda_1,\cdots,\lambda_n\}\in R$

$$\begin{aligned} &由特商公式\lambda=\frac{X^HAX}{\vert X \vert^2}，其中X\neq 0，为\lambda的特征向量\\ &其中\vert X \vert\ge 0 ，为实数.\\ &\therefore 若证\lambda 为实数，即证 X^HAX为实数\\ &已知X^HAX为一维数字，则只需证明(X^HAX)^H=X^HAX即可,\\ &已知A=A^H为Hermite矩阵，(X^HAX)^H=X^HA^HX=X^HAX\in R \end{aligned}$$

c. 特向

若 $A=A^H\in C^{n\times n}$ ，则 $A$ 有 $n$ 个互相正交的特征向量，即 $X_1\bot X_2\bot…\bot X_n$

$$\begin{aligned} &若A为Hermite阵，则\exists U阵Q，使Q^{-1}AQ=Q^HAQ=\Lambda=\left( \begin{matrix} \lambda_1&&\\ &\ddots&\\ &&\lambda_n \end{matrix} \right)\\ &令Q=(X_1,X_2,\cdots,X_n)，且X_1\bot X_2\bot...\bot X_n,\\ &AQ=Q\Lambda\iff \left( \begin{matrix} AX_1&&\\ &AX_2&&\\ &&\ddots&\\ &&&AX_n \end{matrix} \right)=\left( \begin{matrix} \lambda_1X_1&&&\\ &\lambda_2X_2&&\\ &&\ddots&\\ &&&\lambda_nX_n \end{matrix} \right)\\ &即X_i为矩阵A的\lambda_i的特征向量 \end{aligned}$$

1.11.2 Hermite分解定理(对角阵)

若 $A=A^H$ 是Hermite阵，则存在优阵 $Q$ ,使 $Q^{-1}AQ=Q^HAQ=\Lambda=\left(\begin{matrix}\lambda_1&\quad&\quad\\\quad&\ddots&\quad\\\quad&\quad&\lambda_n\end{matrix}\right)$ $A=Q\Lambda Q^{-1} = Q\Lambda Q^H$ ，且 $\lambda(A)\in R$

a. 证明

$$\begin{aligned} &由许尔公式\Rightarrow 有U阵Q使Q^{-1}AQ=Q^HAQ=B\\ &=\left( \begin{matrix} \lambda_1&*&\cdots&*\\ 0&\lambda_2&\cdots&*\\ \vdots&\vdots &\ddots&\vdots\\ 0&0 &\cdots&\lambda_n\\ \end{matrix} \right)\\ &由A是Hermite矩阵，则A^H=A,(Q^HAQ)^H=Q^HA^HQ=Q^HAQ\\ &=\left( \begin{matrix} \overline{\lambda_1}&0&\cdots&0\\ *&\overline{\lambda_2}&\cdots&0\\ \vdots&\vdots &\ddots&\vdots\\ *&* &\cdots&\overline{\lambda_n}\\ \end{matrix} \right)\\ &由此可见，B为对角阵，且 \lambda_i 为实数 \end{aligned}$$

b. 推论

若 $A^H=A$ 是Hermite矩阵，则特征根都是实数，$\{\lambda_1,\cdots,\lambda_n\}\in R$

证明：

$$\begin{aligned} &由特商公式\lambda=\frac{X^HAX}{\vert X \vert^2}，其中X\neq 0，为\lambda的特征向量\\ &其中\vert X \vert\ge 0 ，为实数.\therefore 若证\lambda 为实数，即证 X^HAX为实数\\ &已知X^HAX为一维数字，则只需证明(X^HAX)^H=X^HAX即可,\\ &已知A=A^H为Hermite矩阵，(X^HAX)^H=X^HA^HX=X^HAX\in R \end{aligned}$$

1.11.3 $A^HA$ 型Hermite矩阵

任一矩阵 $A_{n\times p}，A^HA与AA^H$ 都是Hermite矩阵

$$\begin{aligned} &(A^HA)^H=A^HA,(AA^H)^H=A \end{aligned}$$

a. 向量 $X^HX$ 的迹

$$\begin{aligned} &X=\left( \begin{matrix} x_1\\ x_2\\\vdots \\x_n \end{matrix} \right),X^H=(\overline{x_1},\overline{x_2},\cdots,\overline{x_n})\\ &tr(X^HX)=tr(XX^H)=\mid x_1 \mid^2+\mid x_2 \mid^2+\cdots\mid x_n \mid^2=\sum \mid x_j \mid^2 \end{aligned}$$

推论

$$\begin{aligned} tr(XY^H)=tr(Y^HX)=x_1\overline{y_1}+\cdots+x_n\overline{y_n} =\sum\limits_{i=1}\limits^{n}x_i\overline{y_i} \end{aligned}$$

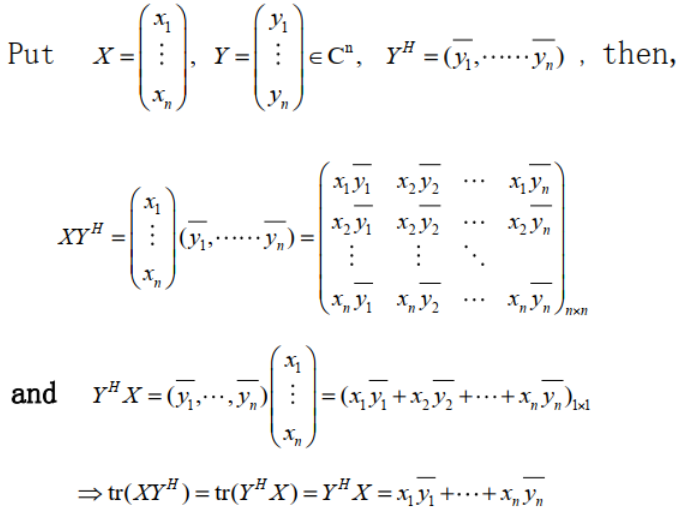
b. $A^HA$ 矩阵的迹

$A_{n\times p}=\left(\begin{matrix}a_{11}&\cdots&a_{1p}\\\vdots&\ddots&\vdots\\a_{n1}&\cdots&a_{np}\end{matrix}\right)\in C^{n\times p}$ ，$A^H_{p\times n}=\left(\begin{matrix}\overline{a_{11}}&\cdots&\overline{a_{n1}}\\\vdots&\ddots&\vdots\\\overline{a_{1p}}&\cdots&\overline{a_{np}}\end{matrix}\right)\in C^{p\times n}$

$$\begin{aligned} &AA^H=\left( \begin{matrix} a_{11}&\cdots&a_{1p}\\ \vdots&\ddots&\vdots\\ a_{n1}&\cdots&a_{np} \end{matrix} \right)\left( \begin{matrix} \overline{a_{11}}&\cdots&\overline{a_{n1}}\\ \vdots&\ddots&\vdots\\ \overline{a_{1p}}&\cdots&\overline{a_{np}} \end{matrix} \right)\\ &=\left( \begin{matrix} a_{11}\overline{a_{11}}+a_{12}\overline{a_{12}}+\cdots+a_{1p}\overline{a_{1p}}&\quad &\quad&\ast\\ \quad&a_{21}\overline{a_{21}}+a_{22}\overline{a_{22}}+\cdots+a_{2p}\overline{a_{2p}}&\quad&\quad\\ \quad &\quad &\ddots&\quad\\ \ast &\quad&\quad&a_{n1}\overline{a_{n1}}+a_{n2}\overline{a_{n2}}+\cdots+a_{np}\overline{a_{np}} \end{matrix} \right) \end{aligned}$$ $$\begin{aligned} &tr(A^HA)=tr(AA^H)=\\ &(\mid a_{11} \mid^2+\mid a_{12} \mid^2+...+\mid a_{1p} \mid^2)+(\mid a_{21} \mid^2+\mid a_{22} \mid^2+...+\mid a_{2p} \mid^2)+\\ &...+(\mid a_{n1} \mid^2+\mid a_{n2} \mid^2+...+\mid a_{np} \mid^2) =\sum\limits_{i=1,j=1}\limits^{n}\mid a_{ij} \mid^2 \end{aligned}$$

推论

$tr(AB^H)=tr(B^HA)=\sum a_{ij}\overline{b_{ij}}$

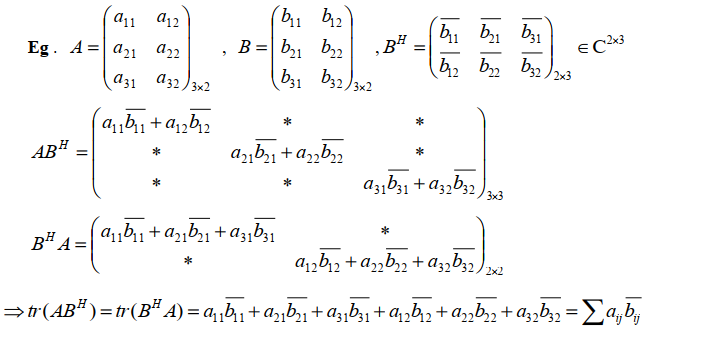
• 将 A、B 矩阵按列分块，可验证 $tr(B^HA)$

  $$\begin{aligned} &A=(\alpha_1,\alpha_2),B=(\beta_1,\beta_2),B^H=\left( \begin{matrix} \overline{\beta_1}^T\\ \overline{\beta_2}^T\\ \end{matrix} \right)\\ &B^HA=\left( \begin{matrix} \overline{\beta_1}^T\\ \overline{\beta_2}^T\\ \end{matrix} \right)(\alpha_1,\alpha_2)=\left( \begin{matrix} &\overline{\beta_1}^T\alpha_1\quad &\overline{\beta_1}^T\alpha_2\\ &\overline{\beta_2}^T\alpha_1\quad &\overline{\beta_2}^T\alpha_2 \end{matrix} \right)\\ &tr(B^HA)=\overline{\beta_1}^T\alpha_1+\overline{\beta_2}^T\alpha_2=\\ &\quad (a_{11}\overline{b_{11}}+a_{21}\overline{b_{21}}+a_{31}\overline{b_{31}})+ (a_{12}\overline{b_{12}}+a_{22}\overline{b_{22}}+a_{32}\overline{b_{32}})\\ &=\sum a_{ij}\overline{b_{ij}} \end{aligned}$$

• 将 A、B 矩阵按行分块，可验证 $tr(AB^H)$

  $$\begin{aligned} &A=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \alpha_3 \end{matrix} \right), B=\left( \begin{matrix} \beta_1\\ \beta_2\\ \beta_3 \end{matrix} \right)，B^H=(\overline{\beta_1}^T,\overline{\beta_2}^T,\overline{\beta_3}^T)\\ &AB^H=\left( \begin{matrix} \alpha_1\\ \alpha_2\\ \alpha_3 \end{matrix} \right)(\overline{\beta_1}^T,\overline{\beta_2}^T,\overline{\beta_3}^T)=\left( \begin{matrix} \alpha_1\overline{\beta_1}^T\quad&\alpha_1\overline{\beta_2}^T\quad&\alpha_1\overline{\beta_3}^T\\ \alpha_2\overline{\beta_1}^T\quad&\alpha_2\overline{\beta_2}^T\quad&\alpha_3\overline{\beta_3}^T\\ \alpha_3\overline{\beta_1}^T\quad&\alpha_3\overline{\beta_2}^T\quad&\alpha_3\overline{\beta_3}^T \end{matrix} \right)\\ &tr(AB^H)=(a_{11}\overline{b_{11}}+a_{12}\overline{b_{12}})+(a_{21}\overline{b_{21}}+a_{22}\overline{b_{22}})+(a_{31}\overline{b_{31}}+a_{32}\overline{b_{32}})\\ &\quad\quad\quad\quad = \sum a_{ij}\overline{b_{ij}} \end{aligned}$$

1.12 二次型

1.12.1 Hermite二次型定义

令 $A^H=A\in C^{n\times n}$ ，$X=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)$ ，称 $X^HAX=\left(\overline{x_1},\overline{x_2},\cdots,\overline{x_n}\right)A\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)$ ，为矩阵 $A$ 产生的二次型，记为 $f(x)=X^HAX$

1.13.2 正定二次型与正定阵定义

若 $A^H=A$ ,对一切 $X\neq 0$ ,有 $X^HAX>0$ ,则 $f(x)=X^HAX$ 为正定二次型，A为正定阵，记为 $A>0$
若 $A^H=A$ ,对一切 $X\neq 0$ ，有 $X^HAX\ge 0$ ,则 $f(x)=X^HAX$ 为半正定二次型，A为半正定阵，记为 $A\ge 0$

1.13 矩阵合同

若 $P^HAP=B(P可逆)$ ,则 $A$ 与 $B$ 合同，记为 $A\overset{\Delta}{=}B$

1. 对称性: $A\overset{\Delta}{=}B\iff B\overset{\Delta}{=}A$
2. 传递性: $A\overset{\Delta}{=}B,B\overset{\Delta}{=}C\iff A\overset{\Delta}{=}C$

1.13.1 合同保正定

若 $A$ 与 $B$ 合同，且 $A$ 是正定阵，则 $B$ 也是正定阵

• 相似与合同都能生成新的矩阵，相似不保持正根，合同保持正根

证明：

$$\begin{aligned} &由A\overset{\Delta}{=}B,且X^HAX>0，若证B为正定阵，即证存在可逆阵Y，使得Y^HBY>0\\ &令Y=P^{-1}X，则X=PY,代入二次型XAX=(PY)^HA(PY)=Y^HP^HAPY\\ &=Y^HBY>0\\ &\therefore B>0为正定阵 \end{aligned}$$

1.13.2 对角正定阵一定合同于单位阵

1.14 正定阵

1.14.1 正定阵的定理

$A>0\iff$ $A$ 为Hermite阵，且 $\lambda_1,\lambda_2,\cdots,\lambda_n > 0$
$A\ge 0 \iff$ $A$ 为Hermite阵，且 $\lambda_1,\lambda_2,\cdots,\lambda_n \ge 0$

---

证明

$\Rightarrow$

若 $A$ 为正定阵，则 $A$ 生成的二次型 $f(x)=X^HAX>0$ ，$\therefore \lambda_i=\frac{X^HAX}{\vert X\vert^2}>0$

$\Leftarrow$

$$\begin{aligned} &由Hermite分解定理，A为Hermite阵，则存在U阵Q，\\ &使得Q^HAQ=\Lambda=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\quad\\ &\quad&\lambda_n\\ \end{matrix} \right)\\ &\therefore A\overset{\Delta}{=}\Lambda,而\lambda_i>0，\Lambda 为正定阵，故A为正定阵 \end{aligned}$$

单位阵是正定阵 ：$\lambda_i= 1$ 显然大于0

1.14.2 正定阵间必合同

1. $A>0（正定阵） \iff A\overset{\Delta}{=}\Lambda$
2. $\Lambda\overset{\Delta}{=}I$ 对角阵一定合同于单位阵
3. 若A,B为同阶正定阵，则 $A\overset{\Delta}{=} B$

证明1：

$$\begin{aligned} &若A正定，则有A^H=A\\ &由Hermite分解定理，必\exists 优阵Q使得Q^HAQ=\Lambda,且\lambda_i>0\\ \end{aligned}$$

证明2：

$$\begin{aligned} 若\Lambda&=\left( \begin{matrix} \lambda_1&\quad&\quad\\ &\ddots&\\ &&\lambda_n \end{matrix} \right),其中\lambda_i>0\\ &\Rightarrow f(x)=X^H\Lambda X=\lambda_1\vert x_1\vert^2+\lambda_2\vert x_2\vert^2+\cdots+\lambda_n\vert x_n\vert^2>0\\ &\Rightarrow 可分解为\Lambda=\left( \begin{matrix} \sqrt{\lambda_1}&\quad&\quad\\ \quad&\ddots&\quad\\ \quad&\quad&\sqrt{\lambda_n}\\ \end{matrix} \right)I\left( \begin{matrix} \sqrt{\lambda_1}&&\\ &\ddots&\\ &&\sqrt{\lambda_n}\\ \end{matrix} \right)\\ &\quad \quad\quad\quad\quad \quad \quad=PIP\\ &可知P可逆，且P^H=P,故P^HIP=\Lambda\\ &即对角正定阵合同于单位阵，记为\Lambda\overset{\Delta}{=}I \end{aligned}$$

证明3：

$$\begin{aligned} &由A>0,B>0,则A\overset{\Delta}{=}I,B\overset{\Delta}{=}I\Rightarrow A\overset{\Delta}{=}B \end{aligned}$$

1.14.3 乘积形式的正定阵

1. 对一切矩阵 $A=A_{n\times p}$ 且 $n\ge p$ ，$A^HA$ 与 $AA^H$ 都是Hermite阵
2. $A^HA$ 与 $AA^H$ 只相差 $n-p$ 个0根
3. $A^HA\ge0$ ，$A^HA\ge 0$
4. $r(A^HA)=r(AA^H)=r(A)$

---

a. $A^HA$ 为Hermite阵

$$\begin{aligned} (A^HA)^H=A^HA，且(AA^H)^H=AA^H，则A^HA与AA^H为Hermite阵 \end{aligned}$$

b. $A^HA与AA^H$ 相差n-p个0根

$$\begin{aligned} &A=A_{n\times p},B={p\times n},且n\ge p\\ &由换位公式 \vert \lambda I-AB\vert=\lambda^{n-p}\vert \lambda I-BA \vert,\\ &则 AB与BA必有相同的非零根，故A^HA与AA^H只相差n-p个零根 \end{aligned}$$

c. $A^HA与AA^H$ 是半正定阵（不是方阵的正定阵）

$$\begin{aligned} &对任意非零向量X，有二次型f(x)=X^HA^HAX=(AX)^H(AX)=\vert AX \vert^2\ge 0,\\ &可知f(x)为半正定二次型，A^HA为半正定阵 \end{aligned}$$

d. $r(AA^H)=r(A^HA)=r(A)$

$$\begin{aligned} &由A^HA为半正定阵，则A^HA与AA^H都只有非负根\\ &可写为\lambda(A^HA)=\{\lambda_1,\lambda_2,...\lambda_p\}\ge 0\\ &由换位公式，知\lambda{A^HA}与\lambda{AA^H}只相差n-p个零根\\ &\therefore \lambda(AA^H)=\{\lambda_1,\lambda_2,...,\lambda_p,0,0,...,0\}\ge 0\\ &r(A^HA)=r(AA^H)=p=r(A)=r(A^H) \end{aligned}$$ $$\begin{aligned} &齐次方程组AX=0,A^HAX=0，解集相同(同解)\\ &若(A^HA)X=0成立，则\vert AX \vert^2=(AX)^H(AX)=X^HA^HAX=(AX)^2=0\\ &\therefore AX=0,r(A^HA)=r(A) \end{aligned}$$

1.15 矩阵的秩

1. 若 $A=A_{n\times p},n>p$ ，(列满秩)，即 $r(A)=p\le n$

   $r(A^HA)=p=r(A)=r(AA^H)$

   $r(A)=r(A^H)=r(\overline{A})$

2. 矩阵秩越乘越小：$r(AB)<min\{r(A),r(B)\}$

1.16 幂0阵

1.16.1 条件

$A^k=0(k\ge 2)$ ，且 $A\neq 0$ ，则为 $k$ 次幂0阵

• 若 $(A-bI)^k=0$ ，$A\neq bI$ ，则 $A$ 为平移幂0阵

1.16.2 特根特向

若 $A^k=0$ ，则 $\lambda(A)=\{0\}$

• 由 Cayley 定理，$\lambda^k=0\Rightarrow \lambda=0$
• 由特向(4.1)求法，$A\cdot A=0$ ，则 $A$ 中各列都是0根的特向

若 $(A-bI)^k=0\Rightarrow \lambda(A)=\{b,\cdots,b\}$

1.16.3 幂0阵不是单阵

$$\begin{aligned} &设A^k=0(A\neq 0) ，假设A为单阵，\Rightarrow P^{-1}AP\xlongequal{相似}D=\left( \begin{matrix} \lambda_1\\&\ddots\\&&\lambda_n \end{matrix} \right)=0\\ &与A\neq 0 矛盾，故A为幂0阵，则非单阵 \end{aligned}$$

推论：$A$ 与 $A-bI$ 同为单阵或非单阵，则 平移不改变单阵或非单阵

• 若 $(A-bI)^k=0$ 且 $A-bI\neq 0$ 则A非单阵 ，且 $\lambda(A)=\{b,b,\cdots,b\}$

  则 $f(A)=f(b)I+\frac{f’(b)}{1!}(A-bI)+\frac{f’’(b)}{2!}(A-bI)^2+\cdots \frac{f^{k-1}(b)}{(k-1)!}(A-bI)^{k-1}$ 为 $f(x)$ 的解析式

1.16.4 记忆：平方幂0

若 $A^2=0(A\neq 0)$ ，则A中列都是0根特向

• A中列 $\left(\begin{matrix}1\-1\end{matrix}\right),\left(\begin{matrix}1\\1\end{matrix}\right)$ 为 $\lambda=0$ 的特向

eg

$$A=\left( \begin{matrix} 3&1\\-1&1 \end{matrix} \right)$$ $$\begin{aligned} &A-2I=\left( \begin{matrix} 1&1\\-1&-1 \end{matrix} \right),则0为A-2I的特根，其特向为\left(\begin{matrix}1\\1\end{matrix}\right),\left(\begin{matrix}1\\-1\end{matrix}\right) \\ &\Rightarrow A的特向为\{2,2\},其特向为 \left(\begin{matrix}1\\1\end{matrix}\right),\left(\begin{matrix}1\\-1\end{matrix}\right) \end{aligned}$$

1.17 幂等阵性质

幂等条件：$A^2=A$

特根：$\lambda(A)=1或0$

$$\begin{aligned} &由Cayley定理，\lambda^2=\lambda\Rightarrow \lambda=1或0,可写全体特根\lambda(A)=\{\underbrace{1,\cdots,1}_{(r)个1},\underbrace{0,\cdots,0}_{(n-r)个0}\} \end{aligned}$$

1.17.1 幂等阵一定为单阵(相似于对角阵)

$A\sim D=\left(\begin{matrix}1\\&\ddots\\&&1\\&&&0\\&&&&\ddots\\&&&&&0\end{matrix}\right)$

单阵引理：

• $f(x)$ 为A的0化式，若 $f(A)=0$ ,且f(x)无重根，则A为单阵 $$\begin{aligned} &若A^2=A\Rightarrow A^2-A=0或A(A-I)=0,则A有0化式f(x)=x^2-x，无重根,故A为单阵 \end{aligned}$$

1.17.2 r(A)与r(I-A)关系

若 $A^2=A$ ，则 $r(A)+r(I_n-A)=n$

$$\begin{aligned} &由于 A(A-I)=0\Rightarrow r(A)+r(A-I)\le n\iff r(A)+r(I_n-A)\le n\\ &又 I=A+(I-A)，n=r(I)=r(A+(I-A))\le r(A)+r(I-A)\le n\\ &\therefore r(A)+r(I_n-A)=r(A)+r(A-I_n)=n \end{aligned}$$

1.18.3 A幂等$\iff$ I-A幂等

$A^2=A\iff (I-A)^2=(I-A)$

• 则有 $tr(I-A)=tr(I)-tr(A)=n-r=r(I-A)$

证明：

$$\begin{aligned} &A^2=A\Rightarrow (I-A)^2=I^2-2A+A^2=I-A\\ \end{aligned}$$

1.18.4 幂等阵的特向

A是幂等阵，则 $A$ 有 $n$ 个无关特向

$$\begin{aligned} &设特根0的特向为X_0,AX_0=0,则齐次方程线性无关解的个数为n-r(A)\\ &设特根1的特向为X_1,AX_1=X_1\iff (A-I)X_1=0，则齐次方程线性无关解的个数为 n-r(I-A)=r(A)\\ &故特向有n个 \end{aligned}$$

1.18.5 谱分解中谱阵为幂等阵

谱分解 $A=\lambda_1G_2+\cdots+\lambda_kG_k$ 中 $G_i$ 为幂等阵（$G_1^2=G_1,\cdots,G_k^2=G_k$）