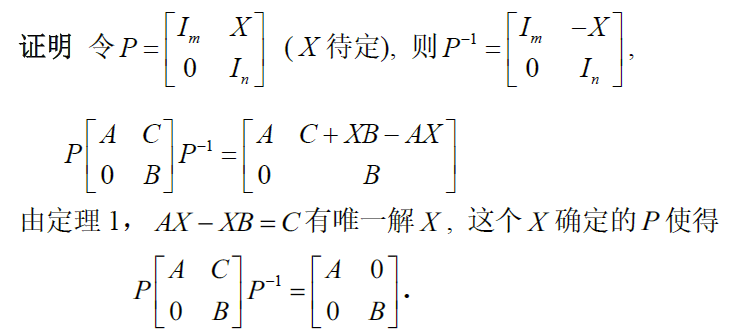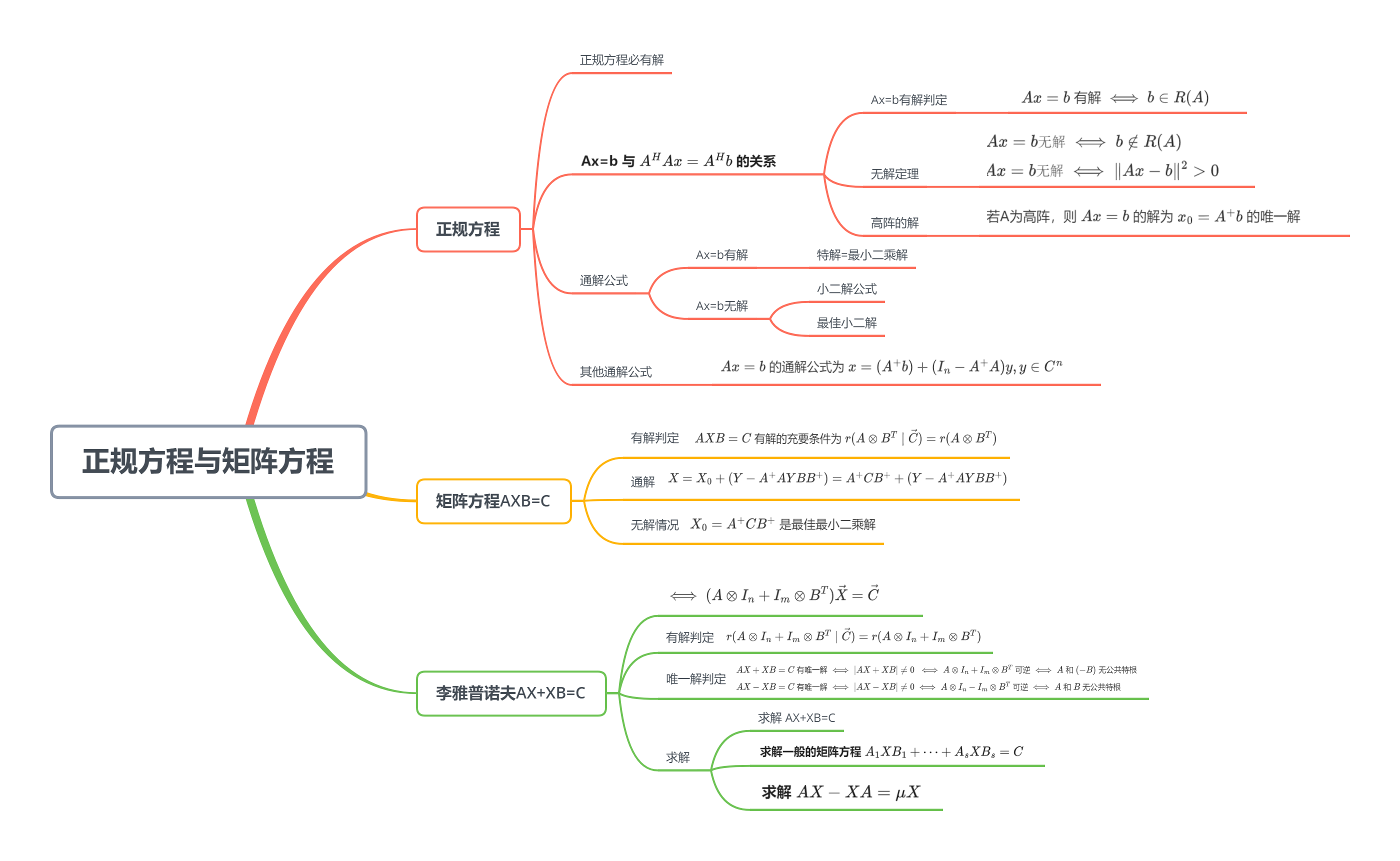
6.1 正规方程
6.1.1 正规方程必有解
正规方程 $A^HAx=A^Hb$ 必有解 ,且特解为 $x_0=A^+b$ ,使 $A^HAx_0=A^Hb$
证明
推论
若矩阵方程 $AXD=B$ 有解,则有特解 $X_1=A^+BD^+$
6.1.2 Ax=b 与 $A^HAx=A^Hb$ 的关系
a. $Ax=b$ 有解判定
若 $Ax=b$ 有解(相容),则可知 $b\in R(A)=\{y=Ax\vert x\in C^n\}$ ,即 $Ax=b$ 有解 $\iff$ $b\in R(A)$
b. 无解定理
c. 高阵的解
若 $A=A_{m\times n}$ 为列满秩阵,则有 $N(A)=\{\vec{0}\}$ ,即 $AX=0$ 只有零解 $X=\vec{0}$

若A为高阵,则 $Ax=b$ 的解为 $x_0=A^+b$ 的唯一解
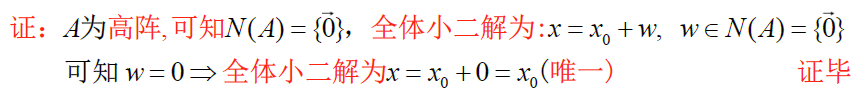
eg
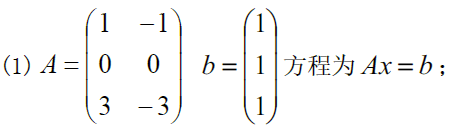

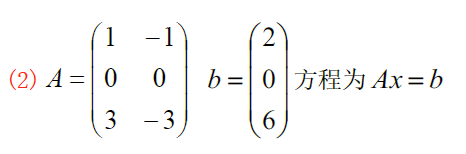

6.1.3 通解公式
a. $Ax=b$ 有解情形
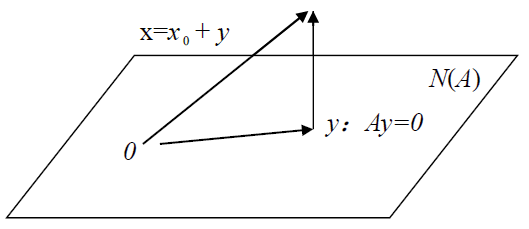
设 $Ay=0$ 基本解为 $Y_1,Y_2,\cdots,Y_k$ ,则 $Ay=0$ 有通解,$y=t_1Y_1+t_2Y_2+\cdots+t_kY_k$ ,可写 $N(A)=\{y\vert Ay=0\}=\{全体y=t_1Y_1+t_2Y_2+\cdots+t_kY_k\}$
且 $Ay=b$ 通解公式为 $x=x_0+(t_1Y_1+t_2Y_2+\cdots+t_kY_k)\xlongequal{\Delta}x_0+y,\forall y\in N(A)$ ,k=n-r(A)
最小二乘解
若 $Ax=b$ 有解,则哪个解x的长度平方 $\vert x\vert^2=x^Hx=\vert x_1\vert^2+\cdots+\vert x_k\vert^2$ 最小:$x_0=A^+b$

eg
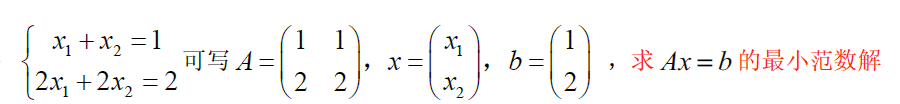
b. $A x=b$ 无解情形
若 $Ax=b$ 无解,则 $\vert Ax-b\vert^2>0$ ,对于 $x\in C^n$ ,如何使 $\vert Ax-b\vert$ 最小:$x_0=A^+b$
若 $\vert Ax_0-b\vert ^2$ 为 $\vert Ax-b\vert^2$ 的最小值,则 $x_0$ 为 $Ax-b$ 的一个极小二乘解,即 $\vert Ax_0-b\vert^2$ 为 $AX$ 与 $b$ 的最小平方距离
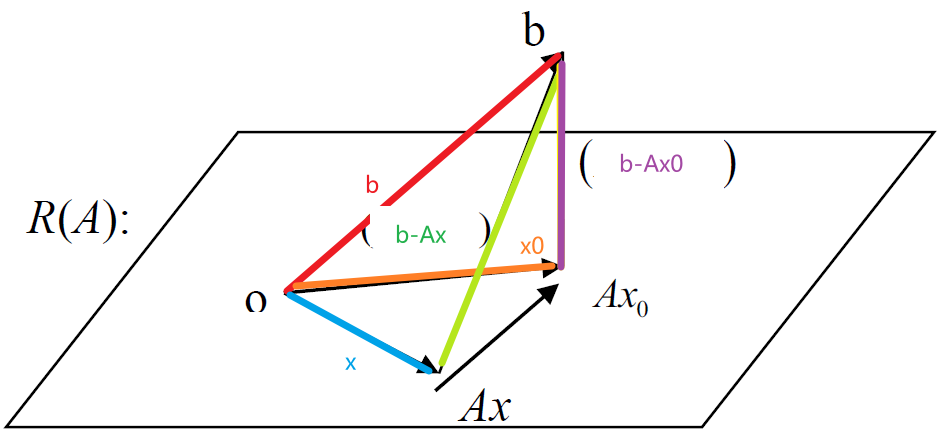
证明
小二解公式
令 $x_0=A^+b$ ,则 $Ax=b$ 的全体小二解为 $x=x_0+Y,Y\in N(A),AY=0$
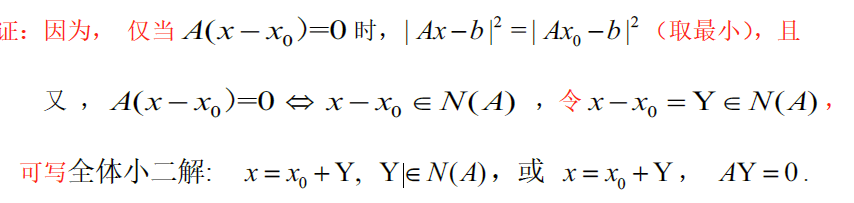
最佳小二解
若 $Ax=b$ 无解,则 $x_0=A^+b$ 为最佳小二解
eg
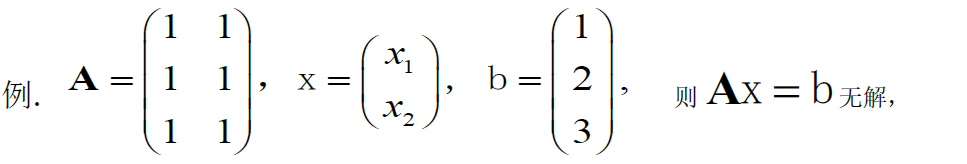
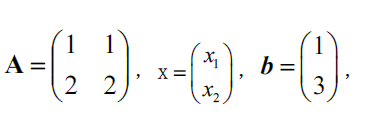
6.1.4 其他通解公式
a. $Ax=0$ 的通解公式
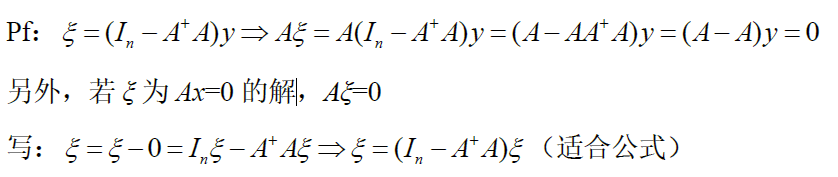
可写核空间公式 $N(A)=\{w=(I-A^+A)y\vert y\in C^n\}$
b. $Ax=b$ 的通解
$Ax=b$ 的通解公式为 $x=(A^+b)+(I_n-A^+A)y,y\in C^n$

6.2 矩阵方程AXB=C求解
6.2.1 有解判定
a. 定理
拉直可求解线性矩阵方程 $AXB=C$ ,其中 $A=A_{m\times n},X=X_{n\times p},B=B_{p\times q}$
记 $X=(x_{ij})_{n\times p}$ ,即为 $np$ 个未知量 $x_{ij}$ 的线性方程组
根据拉直公式,则方程 $AXB=C$ 可被拉直为 $(A\otimes B^T)\vec{X}=\vec{C}$
推广:一般的线性矩阵方程 $A_1XB_1+A_2XB_2+\cdots+A_SXB_S=C$
拉直前有解则拉直后也有解
- $AXB=C$ 有解的充要条件为 $r(A\otimes B^T\mid\vec{C})=r(A\otimes B^T)$
- 齐次方程 $AXB=0$ 的基础解系含有 $np-r(A\otimes B^T)=np-r(A)r(B)$ 个无关向量
b. 有解与唯一解条件

6.2.2 AXB=C求解
a. 有解情况
若矩阵方程 $AXB=C$ 有解相容,则有特解 $X_0=A^+CB^+$
无解定理:若 $X_0=A^+CB^+$ ,使 $AX_0B\neq C$ ,则矩阵方程无解
齐次方程 $AXB=0$ 的通解公式为:$X=Y-A^+AYBB^+$ Y为任一矩阵
- 矩阵方程 $AXB=C$ 的通解公式为:$X=X_0+(Y-A^+AYBB^+) = A^+CB^++(Y-A^+AYBB^+)$
$AXA=A$必有解,特解为 $X_0=A^+AA^+=A^+$,通解为 $X=X_0+(Y-A^+AYAA^+)$
eg
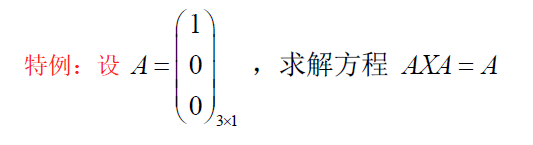
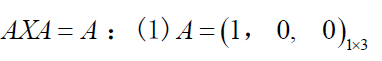
b. 无解情况
若矩阵方程 $AXB=C$ 无解,矩阵 $X=(x_{ij})_{p\times q}$ 的欧式范数或模长记为 $\Vert X\Vert=\Vert X\Vert_F=\sqrt{\sum\vert x_{ij}\vert^2}=\sqrt{tr(X^HX)}$
定理1:若矩阵方程 $AXB=C$ 有解(相容),则 $X_0=A^+CB^+$ 是最小范数解,即 $AXB=C$ 的通解满足 $\Vert X\Vert^2\ge \Vert X_0\Vert^2(最小模长)$
定理2 :若矩阵方程 $AXB=C$ 无解(不相容),则 $X_0=A^+CB^+$ 是最佳最小二乘解,即任一 $X$ 满足 $\Vert AXB-C\Vert^2\ge \Vert AX_0B-C\Vert^2(最小误差)$
6.2.3 AX+XB=C(里亚普诺夫)
$AX+XB=C$ ,其中 $A\in C^{m\times m}.B\in C^{n\times n},X\in C^{m\times n}$
使用拉直公式
$AX+XB=C\iff (AXI_n+I_mXB)=C\iff(\overrightarrow{AXI_n+I_mXB})=\vec{C}\\\iff(A\otimes I_n+I_m\otimes B^T)\vec{X}=\vec{C}$
有解的充要条件为 $r(A\otimes I_n+I_m\otimes B^T\mid\vec{C})=r(A\otimes I_n+I_m\otimes B^T)$
唯一解充要条件 :$\vert A\otimes I_n+I_m\otimes B^T\vert\neq 0$
根据特征值计算 $\vert A\otimes I_n+I_m\otimes B^T\vert$
定理1:
- $AX+XB=C$ 有唯一解 $\iff \vert AX+XB\vert \neq 0$ $\iff A\otimes I_n+ I_m\otimes B^T$ 可逆 $\iff A$ 和 $(-B)$ 无公共特根
- $AX-XB=C$ 有唯一解 $\iff \vert AX-XB\vert \neq 0$ $\iff A\otimes I_n- I_m\otimes B^T$ 可逆 $\iff A$ 和 $B$ 无公共特根
若 $A=A_{m\times m}$ 的特根为 $\lambda_1,\lambda_2,\cdots,\lambda_m$ ; $B=B_{n\times n}$ 的特根为 $t_1,t_2,\cdots,t_n$
则 $A\otimes I_n+I_m\otimes B^T$ 的 $mn$ 个特根为 $\{\lambda_k+t_j\}$ ;$A\otimes I_n-I_m\otimes B^T$ 的 $mn$ 个特征值 $\{\lambda_k-t_j\}$ $(k=1,2,\cdots,m,j=1,2,\cdots,n)$
因为 $B$ 与 $B^T$ 有相同的特征值
$\Rightarrow$ $\vert A\otimes I_n\pm I_m\otimes B^T\vert$ 的 $mn$ 个特征值为 $(\lambda_k\pm t_j)$
$\Rightarrow A\otimes I_n\pm I_m\otimes B$ 不可逆的条件为 无零根 即 $\{\lambda_k\pm t_j\neq 0\}$
$\iff A$ 与 $(\pm B)$ 没有公共特征值
定理2: 若 A 和 B 的特根都有负实部,则 $AX+XB=C$ 有唯一解
- 若特根都在左半平面,则 $A$ 与 $-B$ 不会有公共特根
定理3 :若 $A$ 和 $B$ 分别为 $m$ 阶和 $n$ 阶方阵,若 $A$ 和 $B$ 没有公共特征值,则 $\left[\begin{matrix}A&C\\0&B\end{matrix}\right]$ 与 $\left[\begin{matrix}A&0\\0&B\end{matrix}\right]$ 相似
定理4 :若 $A \in C^{m\times m},B\in C^{n\times n},F\in C^{m\times n}$ ,若 $A$ 和 $B$ 没有公共特根,则 $\left[\begin{matrix}A&0\\F&B\end{matrix}\right]$ 与 $\left[\begin{matrix}A&0\\0&B\end{matrix}\right]$ 相似
- 证明:令 $P=\left(\begin{matrix}I&0\\X&I\end{matrix}\right),P^{-1}=\left(\begin{matrix}I&0\-X&I\end{matrix}\right)$ ,则有许尔公式,$P\left(\begin{matrix}A&0\\F&B\end{matrix}\right)P^{-1}=\left(\begin{matrix}A&0\\XA-BX+F&B\end{matrix}\right)$ ,若为对角阵,则 $AX-BX=-F\Rightarrow AX-BX=F$
a. 求解矩阵方程
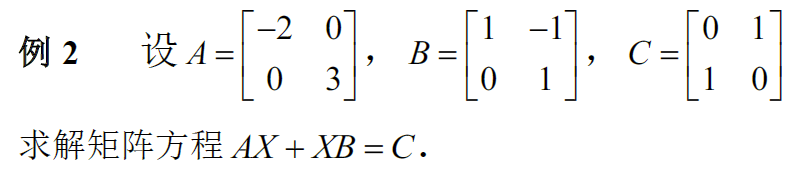
A的特征值为 -2,3;B的特征值为1,1。矩阵方程拉直为 $AX+XB=C\iff(A\otimes I_2+I_2\otimes B^T)\vec{X}=\vec{C}$ 。而 $A$ 与 $-B$ 没有公共特征值,则拉直后方程具有唯一解。

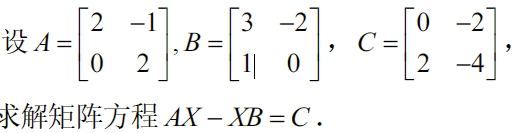
$\lambda(A)=\{2,2\},\lambda(B)=\{1,2\}$ ,故A和B有公共特征值,故解不唯一,
$AX-XB=C$ 可拉直为 $(A\otimes I_{2\times 2}-I_{2\times 2}\otimes B^T)\vec{X}=\vec{C}$ ,有 $X=\left[\begin{matrix}x_1&x_2\\x_3&x_4\end{matrix}\right],\vec{X}=\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right)$
$(A\otimes I_{2\times 2}-I_{2\times 2}\otimes B^T)\vec{X}=\left(\begin{matrix}-1&-1&-1&0\\2&2&0&-1\\0&0&-1&-1\\0&0&2&2\end{matrix}\right)\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right)=\left(\begin{matrix}0\-2\\2\-4\end{matrix}\right) \iff GX=b$ 由于 $r(G\vert b)=r(G)=3$ ,故方程有解,其解为 $(G\vert b)\rightarrow \left(\begin{array}{c:c} \begin{matrix} 1&1&0&0\\ 0&0&1&0\\0&0&0&1\\0&0&0&0 \end{matrix}& \begin{matrix} -4\\ 4\-6\\0 \end{matrix} \end{array}\right)$
故 G 的解为 $X=\left(\begin{matrix}-4\\0\\4\\6\end{matrix}\right)+t\left(\begin{matrix}1\-1\\0\\0\end{matrix}\right)$ 原矩阵方程的解为 $X=\left(\begin{matrix}-4&0\\4&6 \end{matrix}\right)+t\left(\begin{matrix}1&-1\\0&0\end{matrix}\right)$
b. 求解一般的矩阵方程 $A_1XB_1+\cdots+A_sXB_s=C$
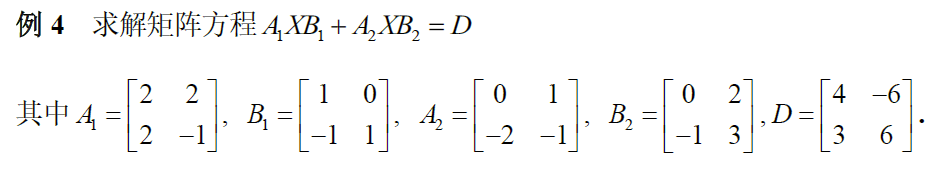

c. 求解 $AX-XA=\mu X$
将方程拉直为 $(A\otimes I_n-I_n\otimes A^T)\vec{X}=\mu \vec{X}$
记 $G=A\otimes I_n-I_n\otimes A^T$ 原方程化为 $G\vec{X}=\mu \vec{X}\Rightarrow (G-\mu I)\vec{X}=0$
有非零解条件为 $\vert G-\mu I\vert=0$ ,即 $\mu$ 是 G的特征值,而 $\lambda(G)=\{\lambda_r-\lambda_s\}$
故 有非零解条件为:$\exists r,s$ ,使 $\mu=\lambda_r-\lambda_s,1\le r,s\le n$

$\lambda(A)=\{1,3\}$,$G=A\otimes I_2-I_2\otimes A^T=\left(\begin{matrix}0&-2&0&0\\0&-2&0&0\\2&0&2&-2\\0&2&0&0\end{matrix}\right)$ $\lambda(G)=\{\lambda(A)_i-\lambda(A)_j\}=\{2,0,0,-2\}$ ,故 $\exist \lambda(G)=\mu=-2$ ,矩阵方程有非零解
$X=\left(\begin{matrix}x_1&x_2\\x_3&x_4\end{matrix}\right)$ ,$\vec{X}=\left(\begin{matrix}x_1\\x_2\\x_3\\x_4\end{matrix}\right)$ ,解 $G\vec{X}=0$ $\Rightarrow \vec{X}=t_1\left(\begin{matrix}-1\\0\end{matrix}\right)+t_2\left(\begin{matrix}1\\0\end{matrix}\right)=\left(\begin{matrix}-t_1&t_2\\0&0\end{matrix}\right)$ ,故原矩阵方程的解 $X=\left(\begin{matrix}-t_1\\t_2\\0\\0\end{matrix}\right)$

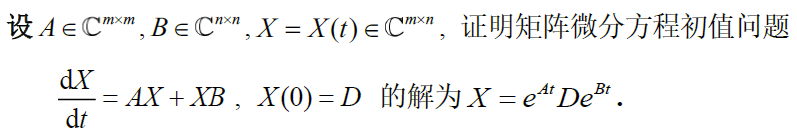
由拉直公式 $\frac{dX}{dt}=AX+XB=(A\otimes I_n+I_m\otimes B^T)\vec{X}=\vec{C}$