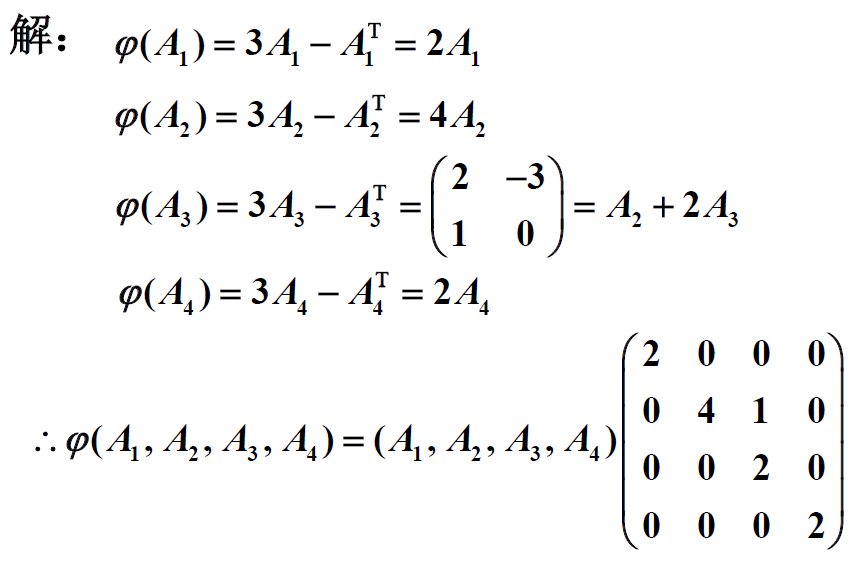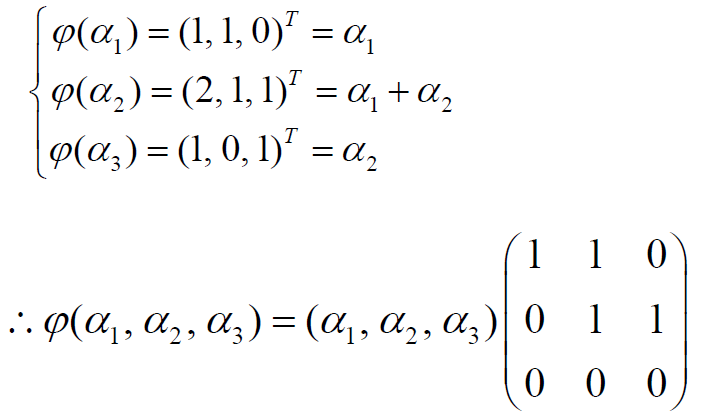
5.1 线性空间概念
5.1.1 定义与性质
数域:含0和1,且对加减乘除封闭的数集
a. 定义
设 $V$ 是一个非空集合,其元素为 $x,y,z$ ,$K$ 是一个数域,如果 $V$ 中元素满足
- $V$ 对加法封闭,即当 $x,y\in V$ 时,有唯一 $x\oplus y\in V$ ,且加法满足:
- 结合律:$(x\oplus y)\oplus z=x\oplus (y\oplus z)$
- 交换律:$x\oplus y=y\oplus x$
- 存在零元素:$x\oplus 0=x$
- 存在负元素:对 $\forall x\in V,\exists y\in V$ ,使 $x\oplus y=0$ ,则称 $y$ 为 $x$ 的负元素,记为 $-x$
- $V$ 对数乘运算封闭,即当 $x\in V,k\in K$ 时,有唯一 $k\circ x\in V$ ,且数乘运算满足
- $1\circ x=x$ (幺元素)
- $k\circ(x\oplus y)=k\circ x\oplus k\circ y$
- $(k+l)\circ x=k\circ x\oplus l\circ x$
- $k\circ(l\circ x)=(k\circ l)\circ x$
则称 $V$ 为数域 $K$ 上的线性空间或向量空间
当 $K=R$ 时,称为实线性空间
当 $K=C$ 时,称为复线性空间
eg
实数域上全体 $n$ 维向量的集合 $R^n=\{\left(\begin{matrix}x_1\\\vdots\\x_n\end{matrix}\right)\vert x_1,\cdots,x_n\in R\}$ , $\alpha=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right),\beta=\left(\begin{matrix}y_1\\y_2\\\vdots\\y_n\end{matrix}\right)\in R^n,k\in R$
- 加法: $\alpha+\beta=\left(\begin{matrix}x_1+y_1\\x_2+y_2\\\vdots\\x_n+y_n\end{matrix}\right)\in R^n$
- 数乘:$k\alpha=\left(\begin{matrix}kx_1\\kx_2\\\vdots\\kx_n\end{matrix}\right)\in R^n$
$R^n$ 是数域 $R$ 上的线性空间
$C^n$ 是数域 $C$ 上的线性空间
正弦函数集合 $S[x]=\{asin(x+b)\vert a,b\in R\}$ ,$s_1,s_2\in S[x]$
加法
数乘
$\therefore S[x]$ 是一个线性空间
设 $R^+$ 为所有正实数组成的数集,加法和数乘定义为:$m\oplus n=mn$ ,$k\circ m=m^k$ ,证: $R^+$ 为 $R$ 上的线性空间
加法: $a\oplus b=ab\in R^+$
$a\oplus b=ab=ba=b\oplus a$
$(a\oplus b)\oplus c=(ab)\oplus c=a(bc)=a\oplus(b\oplus c)$
$R^+$ 中存在零元素1,$\forall a\in R^+$,有 $a\oplus 1=a\cdot 1=a$
$\forall a\in R^+$ ,$a\oplus x=a\cdot x=1\Rightarrow x=a^{-1}$ ,即有负元素 $a^{-1}$
数乘:$\forall k\in R$ ,$ka=a^k\in R^+$
$1\circ a=a^1=a$
$\lambda\circ(\mu\circ a)=\lambda\circ a^\mu=(a^{\mu})^{\lambda}=a^{\lambda\mu}=(\lambda\mu)\circ a$
$(\lambda+\mu)\circ a=a^{\lambda+\mu}=a^{\lambda}a^{\mu}=a^\lambda\oplus a^\mu=\lambda\circ a\oplus\mu \circ a$
$\lambda\circ (a\oplus b)=\lambda\circ (ab)=(ab)^\lambda=a^\lambda b^\lambda=a^\lambda\oplus b^\lambda=\lambda\circ a\oplus \lambda\circ b$
故 $R^+$ 是一个线性空间
b. 性质
线性空间 $V$ 中的元素,有唯一的零元素,任意元素有唯一的负元素
5.1.2 线性空间的基与维数
a. 线性表示
如果 $x_1,\cdots,x_m$ 为线性空间 $V$ 中的 $m$ 个向量,$x\in V$ ,且存在数域 $K$ 中一组数 $c_1,\cdots,c_m$ ,使 $x=c_1x_1+\cdots+c_mx_m$ ,则称 $x$ 为向量组 $x_1,\cdots,x_m$ 的线性组合,即 $x$ 可由 $x_1,\cdots,x_m$ 线性表示
b. 线性相关与线性无关
对于 $x_1,\cdots,x_m\in V$ ,如果存在不全为零的 $m$ 个数 $c_1,\cdots,c_m\in K$ ,使 $c_1x_1+\cdots+c_mx_m=0$ ,则称向量组 $x_1,\cdots,x_m$ 线性相关,否则为线性无关
c. 基与维数
如果 $x_1,\cdots,x_m$ 是线性空间 $V$ 中 $m$ 个元素且满足:
- $x_1,\cdots,x_m$ 线性无关
- $\forall x\in V$ 可由 $x_1,\cdots,x_m$ 线性表示
则 $x_1,\cdots,x_m$ 为 $V$ 的一个基,$m$ 称为 $V$ 的维数,记为 $dim V=m$
维数为 $m$ 的线性空间 $V$ 记为 $V^m$ ,当 $m=+\infty$ 时,称为 无限维线性空间
基性质
设 $V$ 是 $r$ 维子空间 ($dim V=r$) ,则 $W$ 中任 $r+1$ 个向量必线性相关
$V$ 的基 $[\alpha_1,\cdots,\alpha_r]$ 必是向量组 $V$ 的一个极大无关组,从而 $dim V=r(V)$
基的扩充
设 $W$ 是数域 $K$ 上的线性空间 $V^n$ 的一个 $m$ 维子空间,$x_1,\cdots,x_m$ 是 $W$ 的基,则这 $m$ 个基向量必可扩充为 $V^n$ 的一个基
d. 坐标
设线性空间 $V^n$ 的一个基 $x_1,\cdots,x_n,x\in V^n$ ,$x=\xi_1x_1+\xi_2x_2+\xi_nx_n$ ,则称 $\xi_1,\cdots,\xi_n$ 为 $x$ 在该基下的坐标,记为 $(\xi_1,\cdots,\xi_n)^T$
定理 :设 $x_1,\cdots,x_n$ 是 $V^n$ 的一个基,且 $x\in V^n$ ,则 $x$ 可唯一表示为 $x_1,\cdots,x_n$ 的线性组合
e. 基变换与坐标变换
设 $I:x_1,\cdots,x_n;II:y_1,\cdots,y_n$ 是 $V^n$ 的两个基,则有:
有 $(y_1,\cdots,y_n)=(x_1,\cdots,x_n)C$ ,其中矩阵 $C=\left(\begin{matrix}c_{11}&c_{12}&\cdots&c_{1n}\\c_{21}&c_{22}&\cdots&c_{2n}\\\vdots&\vdots&\ddots&\vdots\\c_{n1}&c_{n2}&\cdots&c_{nn}\end{matrix}\right)$ 称为基 $I$ 到基 $II$ 的过渡矩阵
对于同一向量,在不同基下有不同表示方式
则有 坐标变换 $\left(\begin{matrix}\xi_1\\\vdots\\\xi_n\end{matrix}\right)=C\left(\begin{matrix}\eta_1\\\vdots\\\eta_n\end{matrix}\right)$
eg
设矩阵空间 $K^{2\times 2}$ 的两个基
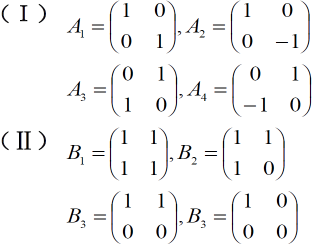
求过渡矩阵
5.2 子空间
5.2.1 定义
设 $W\subset V$ ,$W$ 是数域 $K$ 上的线性空间 $V$ 的一个非空子集合,且
则称 $W$ 为 $V$ 的线性子空间或子空间
平凡子空间 $W=V$ 或 $\varphi=\{0\}$ ;其余称为非平凡子空间
子空间 $W$ 一定含有零向量 $\vec{0} \in W$;若不包含零向量,则不是子空间
- 齐次方程解集 $W(A)=\{X\in C^n\vert AX=0\}$ ,对加法,数乘封闭($AX_1=0,AX_2=0,A(X_1+X_2)=0$),($AX_1 =0$,$A(kX_1)=k(AX_1)=0$) ,且有零向量,故是 $C^n$ 的子空间
- 非齐次方程解集 $W(A)=\{X\in C^n\vert AX=b\neq 0\}$ 不含零向量,故W(A) 不是子空间,且对加法,数乘不封闭
5.2.2 生成子空间
a. 引理
由 $C^n$ 中向量 $\alpha_1,\alpha_2\cdots,\alpha_m$ 的所0有 线性组合生成的向量集合 $W(A)=\{x=k_1\alpha_1+k_2\alpha_2+\cdots+k_m\alpha_m\}$ 是一个子空间,称W为由$\alpha_1,\cdots,\alpha_m$ 生成的子空间,记为 $W=L(\alpha_1,\cdots,\alpha_m)$ 或 $W=span(\alpha_1,\cdots,\alpha_m)$
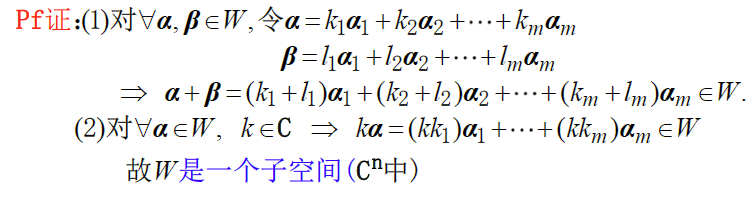
b. 维数公式
$dim (V_1+V_2)=dimV_1+dim V_2-dim(V_1\bigcap V_2)$
c. 子空间的交与和
交:如果 $V_1$ ,$V_2$ 是数域 $K$ 上的线性空间 $V$ 的两个子空间,那么 $V_1\bigcap V_2$ 也是 $V$ 的子空间
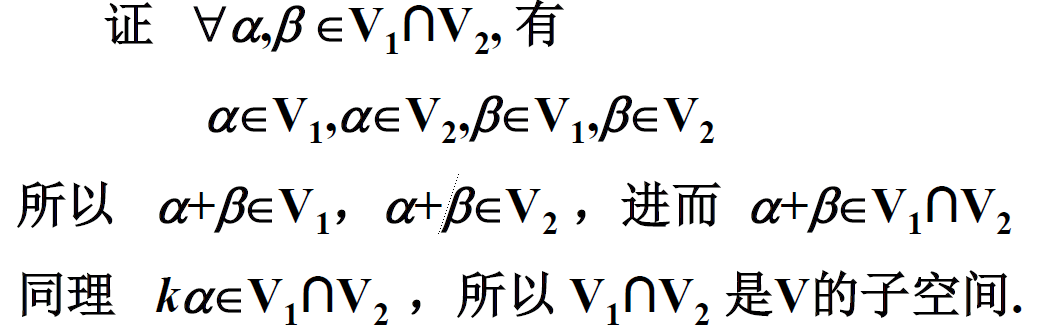
和 :设 $V_1$ ,$V_2$ 都是 $V$ 的子空间,则集合 $\{z\vert z=x+y,x\in V_1,y\in V_2\}$ 称为 $V_1$ 与 $V_2$ 的和,记为 $V_1+V_2$
如果 $V_1$ ,$V_2$ 都是 $V$ 的子空间,则 $V_1+V_2$ 也是 $V$ 的子空间

- $V_1\bigcap V_2$ 是包含在 $V_1$ ,$V_2$ 的最大子空间
- $V_1+V_2$ 是包含 $V_1,V_2$ 的最小子空间
eg
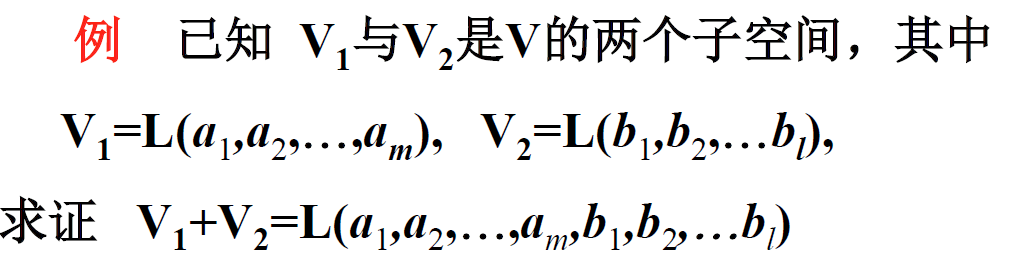
d. 直和
如果 $V_1+V_2$ 中的任一向量只能唯一地表示为$V_1$ 的一个向量和 $V_2$ 中的一个向量的和,则称 $V_1+V_2$ 为 $V_1$ 与 $V_2$ 的直和,记为 $V_1\oplus V_2$
定理:若 $V_1+V_2$ 为直和$\iff V_1\bigcap V_2=L(0)$
- 不存在公共部分,即无法用公共部分的向量代替


推论:
- 设 $V_1$ ,$V_2$ 都是 $V$ 的子空间,则 $V_1+V_2$ 是直和 $\iff dim(V_1+V_2)=dim V_1+dimV_2$
- 如果 $x_1,\cdots,x_k$ 为 $V_1$ 的基,$y_1,\cdots,y_l$ 为 $V_2$ 的基,且 $V_1+V_2$ 为直和,则 $x_1,\cdots,x_k,y_1,\cdots,y_l$ 为 $V_1\oplus V_2$ 的基
eg



5.2.3 A产生的子空间
a. 列空间(值域)
$A=A_{m\times n}$ 的值域 $R(A)=\{全体y=Ax\vert x\in C^n\}\subset C^m$
即对 $C^n$ 中的所有列向量进行 $A$ 变换产生的列生成空间,记为 $R(A)=\{y=x_1\alpha_1+\cdots+x_n\alpha_n\vert X\in C^n\}$
$R(A)=L(\alpha_1,\cdots,\alpha_n)$ 或 $R(A)=span(\alpha_1,\cdots,\alpha_n)$
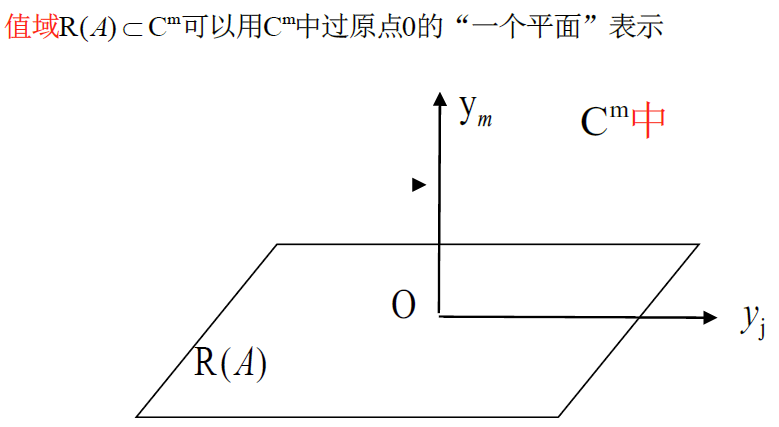
$r(A)=r(\alpha_1,\cdots,\alpha_n)\overset{\Delta}{=}r(A)\Rightarrow 维数:dimR(A)=r(A)(维数=秩数)$
b. A的核空间
前置知识:$AX=0$ 的其他通解形式 $X=(I-A^+A)Y,\forall Y\in C^n$
$A=A_{m\times n}$ 的核空间为 $N(A)=\{X\vert AX=0\}\subset C^n=\{X=(I-A^+A)Y\mid \forall Y\in C^n\}\subset C^n$ (解空间)
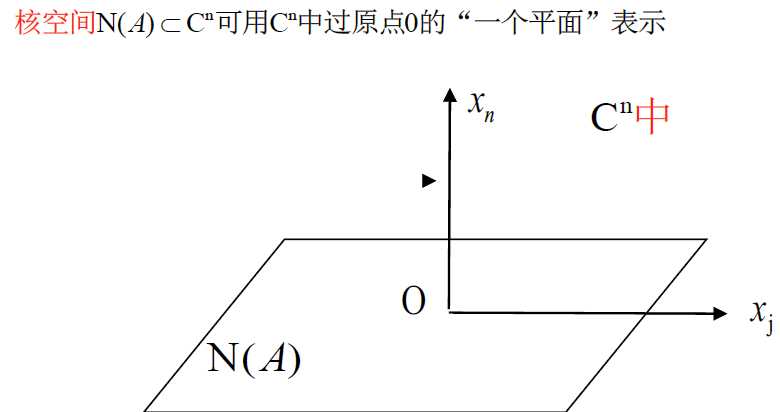
可知,$N(A)=R(I-A^-A)=R(I-A^+A)$ ,则有 $dim N(A)=dim R(I_n-A^-A)=r(I_n-A^+A)$ 由于 $A^-A,A^+A$ 为幂等阵 $r(I_n-A^-A)=r(I_n-A^+A)=n-r(A)$ ,即 $dimN(A)=n-r(A)$
维数公式
$dim N(A)+dim R(A)=n$ 或 $dim N(A)+r(A)=n$ ,即 $dim N(A)=n-r(A)$
c. 正交引理
$C^m$ 中正交引理(列空间中向量的正交向量)
任取 $b\in C^m$ ,令 $x_0=A^+b\in C^n$ ,则 $(b-Ax_0)\bot Ax,\forall x\in C^n$
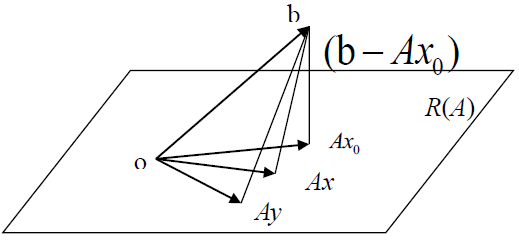

正交子空间
设 $A\in C^{m\times n}$ ,则有 $N(A)\bot R(A^H)$ ,且 $N(A^H)\bot R(A)$
证明:
$A^H\in C^{n\times m}$ ,$R(A^H)\subset C^n$ ,$N(A^H)\subset C^m$ ,$R(A^H)+N(A^H)=C^n$
$C^n$ 中正交引理(核空间的正交向量)
任取 $b\in C^m$ ,令 $x_0=A^+b\in C^n$ ,则 $x_0\bot N(A)$ ,即 $x_0\bot y ,y\in \{y\vert Ay=0\}$
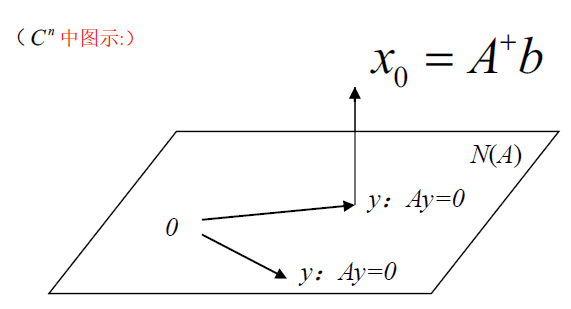
证明:
$x_0=A^+b$ 为 $Ax=b$ 的最小解
5.3 线性映射与自然基分解
同一空间——线性变换
不同空间——线性映射
自然基 :$R^n$ 中的自然基为:
$R^n$ 中每一向量 $\alpha=(a_1,a_2,\cdots,a_n)$ 都有分解公式 $\alpha=a_1\epsilon_1+a_2\epsilon_2+\cdots+a_n\epsilon_n$
映射:设 $S$ 和 $S’$ 是两个集合,存在一个法则 $\sigma:S\rightarrow S’$ ,它使 $S$ 中的每个元素 $a$ 在 $S’$ 中有一个确定的元素 $a’$ 与之对应,记为
称为集合 $S$ 到 $S’$ 的映射, $a’$ 称为 $a$ 在映射 $\sigma$ 下的 象 ,$a$ 为 $a’$ 在映射 $\sigma$ 下的 原象
交换:$S$ 到 $S$ 自身的映射
相等:设 $\sigma_1$ 与 $\sigma_2$ 都是集合 $S$ 到 $S’$ 的映射,如果对于 $\forall a\in S$ ,都有 $\sigma_1(a)=\sigma_2(a)$ ,则称 $\sigma_1$ 与 $\sigma_2$ 相等,记为 $\sigma_1=\sigma_2$
乘法:设 $\sigma$ ,$\tau$ 依次是集合 $S$ 到 $S_1$ ,$S_1$ 到 $S_2$ 的映射 ,乘积 $\tau \sigma$ 定义为$(\tau\sigma)(a)\overset{\Delta}{=}\tau(\sigma(a)),a\in S$ ,$\tau\sigma$ 是 $S$ 到 $S_2$ 的一个映射
- 不满足交换律: $\tau\sigma\neq \sigma \tau$
- 满足结合律:$\mu(\tau\sigma)=(\mu\tau)\sigma$ ($\mu$ 是 $S_2$ 到 $S_3$ 的映射)
5.3.1 定义与性质
设 $W$ 为一个线性空间,且 $\varphi:W\rightarrow R^n$ 是一个映射 $(\alpha,\beta\in W,k\in R)$ ,若满足:
则称 $\varphi$ 为 $W$ 到 $R^n$ 的一个线性映射
性质
零点不变:$\varphi(0)=0$
线性映射保持线性组合结构 :$\varphi(k_1\alpha_1+k_2\alpha_2+\cdots+k_p\alpha_p)=k_1\varphi(\alpha_1)+k_2\varphi(\alpha_2)+\cdots+k_p\varphi(\alpha_p),k_1,k_2,\cdots,k_p\in R$
原象线性相关(无关),则像也线性相关(无关)
5.3.2 应用
- 构造一个线性映射,把未知问题转化为求原象问题
- 写出自然基分解公式,然后找出自然基的原象
- 写出自然基原象的线性组合,可得所求原象

解:令多项式集合 $W=\{f(x)=a_0+a_1x+\cdots+a_{n-1}x^{n-1}\vert a_j\in R,0\le j\le n-1\}$ , $W$ 为一个线性空间,$dim(W)=n$
引入映射 $\varphi:W\rightarrow R^n,\forall f,g\in W$
对于映射 $\varphi$ ,有 $\varphi(f+g)=\varphi(f)+\varphi(g)$ ,$\varphi(kf)=k\varphi(f)$ ,可知 $\varphi$ 为线性映射(不改变组合结构)
设 $f(x)\in W$ 为所求的多项式,满足:$f(x_1)=b_1,f(x_2)=b_2,\cdots,f(x_n)=b_n$
令 $\beta=(b_1,b_2,\cdots,b_n)\in R^n$ ,则有 $\varphi(f)=(f(x_1),f(x_2),\cdots,f(x_n))=(b_1,b_2,\cdots,b_n)=\beta$
即问题转化为求一个 $f$ ,使 $\varphi(f)=\beta=b_1\epsilon_1+b_2\epsilon_2+\cdots+b_n\epsilon_n$ ,其原象 $f_1,f_2,\cdots,f_n\in W$ 使 $\varphi(f_1)=\epsilon_1,\varphi(f_2)=\epsilon_2,\cdots,\varphi(f_n)=\epsilon_n$
则必有 $\varphi(f)=b_1\varphi(f_1)+b_2\varphi(f_2)+\cdots+b_n\varphi(f_n)=b_1\epsilon_1+b_2\epsilon_2+\cdots+b_n\epsilon_n=\beta$
若 $\varphi(f_1)=\epsilon_1=(1,0,\cdots,0)\Rightarrow (f_1(x_1),f_1(x_2),\cdots,f_n(x_n))=(1,0,\cdots,0)\\\Rightarrow f_1(x_1)=1,f_1(x_2)=\cdots=f_1(x_n)=0$
则 $(n-1)$ 次多项式 $f_1$ 恰有 $n-1$ 个根为 $x_2,x_3,\cdots,x_n$ ,可设
同理:
eg


5.4 线性变换
5.4.1 平面内向量绕原点旋转坐标变换
设向量 $V=\left(\begin{matrix}x\\y\end{matrix}\right)$ 旋转 $\theta$ 角后变为 $V’=\left(\begin{matrix}x’\\y’\end{matrix}\right)$ ,$V$ 的倾角为 $\varphi$
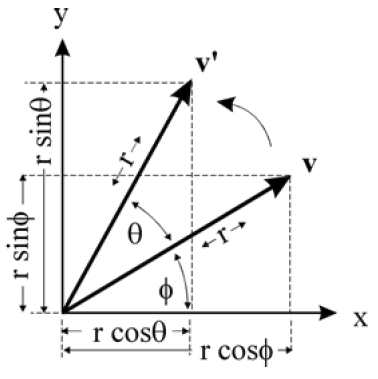
可写
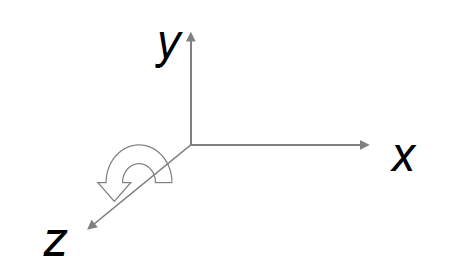
5.4.2 三维空间绕坐标轴旋转坐标变换
a. 绕z轴旋转
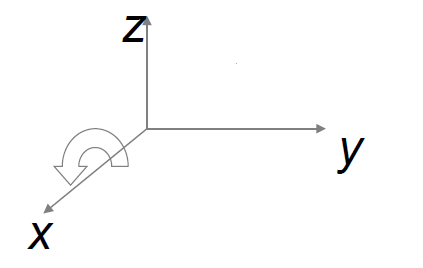
b. 绕x轴旋转
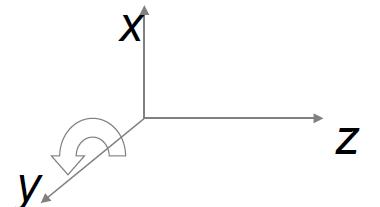
c. 绕y轴旋转
5.4.3 线性变换
设 $V$ 为数域 $K$ 上的线性空间,若变换 $\sigma:V\rightarrow V$ ,对于 $\forall \alpha,\beta\in V,k\in K$ ,满足
则称 $\sigma$ 为空间 $V$ 上的线性变换
a. 性质
$\sigma$ 为 $V$ 的线性变换,则 $\sigma(0)=0$ ,$\sigma(-\alpha)=-\sigma(\alpha)$
线性变换保持线性组合及关系式不变
若 $\beta=k_1\alpha_1+k_2\alpha_2+\cdots+k_r\alpha_r$ ,则 $\sigma(\beta)=k_1\sigma(\alpha_1)+k_2\sigma(\alpha_2)+\cdots+k_r\sigma(\alpha_r)$
线性变换不改变线性相关性,但不保持线性无关性。即
若 $\alpha_1,\alpha_2,\cdots,\alpha_r$ 线性相关,则 $\sigma(\alpha_1),\sigma(\alpha_2),\cdots,\sigma(\alpha_r)$ 线性相关
若 $\alpha_1,\alpha_2,\cdots,\alpha_r$ 线性无关,则 $\sigma(\alpha_1),\sigma(\alpha_2),\cdots,\sigma(\alpha_r)$ 未必无关
b. 复合乘积
设 $\sigma$ ,$\tau$ 为线性空间 $V$ 的两个线性变换,复合乘积为 $\sigma\tau$ :$(\sigma\tau)(\alpha)=\sigma(\tau(\alpha)),\forall \alpha\in V$ ,则 $\sigma\tau$ 也是 $V$ 上的线性变换
- 结合律:$(\sigma\tau)\varphi=\sigma(\tau\varphi)$
- $I\sigma=\sigma I=\sigma$ ,$I$ 为恒等变换
c. 数乘
设 $\sigma$ 为空间 $V$ 的线性变换,定义 $k$ 与 $\sigma$ 的数乘:$(k\sigma)(x)=k\sigma(x),\forall x\in V$ ,则 $k\sigma$ 也是 $V$ 的线性变换
性质:
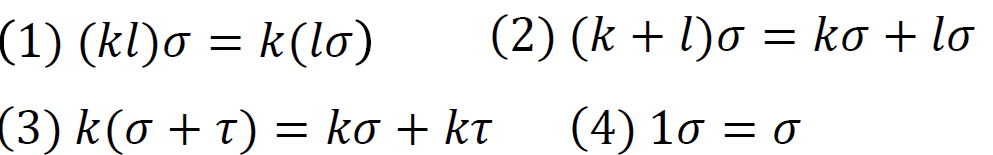
d. 逆线性变换
设 $\sigma$ 为空间 $V$ 的线性变换,若有 $V$ 的变换 $\tau$ 使 $\sigma\tau=\tau\sigma=I$ ,则称 $\sigma$ 为可逆变换,$\tau$ 为 $\sigma$ 的逆变换,记为 $\sigma^{-1}$
- 可逆变换 $\sigma$ 的逆变换 $\sigma^{-1}$ 也是线性变换
- 线性变换 $\sigma$ 可逆 $\iff$ 线性变换 $\sigma$ 是一一对应的
- 设 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 是线性空间 $V$ 的一组基,$\sigma$ 为 $V$ 的线性变换,则 $\sigma$ 可逆当且仅当 $\sigma(\epsilon_1),\cdots,\sigma(\epsilon_n)$ 线性无关
- 可逆线性变换是把 无关向量变成无关向量
5.4.4 线性变换的矩阵表示
设 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 为数域 $F$ 上线性空间 $V$ 的一组基,$\sigma$ 为 $V$ 的线性变换,基向量的像可被基线性表示,即
$\sigma(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)=(\epsilon_1,\epsilon_2,\cdots,\epsilon_n)A$ ,其中 $A=\left(\begin{matrix}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\end{matrix}\right)$
矩阵 $A$ 为线性变换 $\sigma$ 在基 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 下的矩阵
定理:
设 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 为数域 $F$ 上线性空间 $V$ 的一组基,在这组基下,$V$ 的每一个线性变换都与 $F^{n\times n}$ 中的唯一矩阵对应,且具有性质:
- 线性变换的和对应于矩阵的和
- 线性变换的乘积对应于矩阵的乘积
- 线性变换的数量积对应于矩阵的数量积
- 可逆线性变换与可逆矩阵对应,且逆变换对应于逆矩阵
设线性空间 $V$ 上的线性变换 $\varphi$ 在两个基 $\epsilon_1,\epsilon_2,\cdots,\epsilon_n$ 与 $\eta_1,\eta_2,\cdots,\eta_n$ 下的矩阵分别是 $A$ 、$B$ ,则有相似公式 $B=P^{-1}AP$

eg