参考:https://www.bilibili.com/video/BV1mM411r7ko?p=1&vd_source=260d5bbbf395fd4a9b3e978c7abde437
[TOC]
1.1 函数
表示量与量之间的关系:$A=\pi r^2$
一组输入输出关系:一组输入唯一对应一组输出
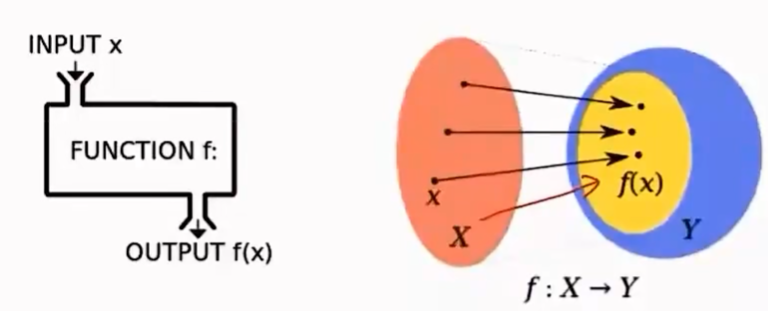
1.1.1 函数分类
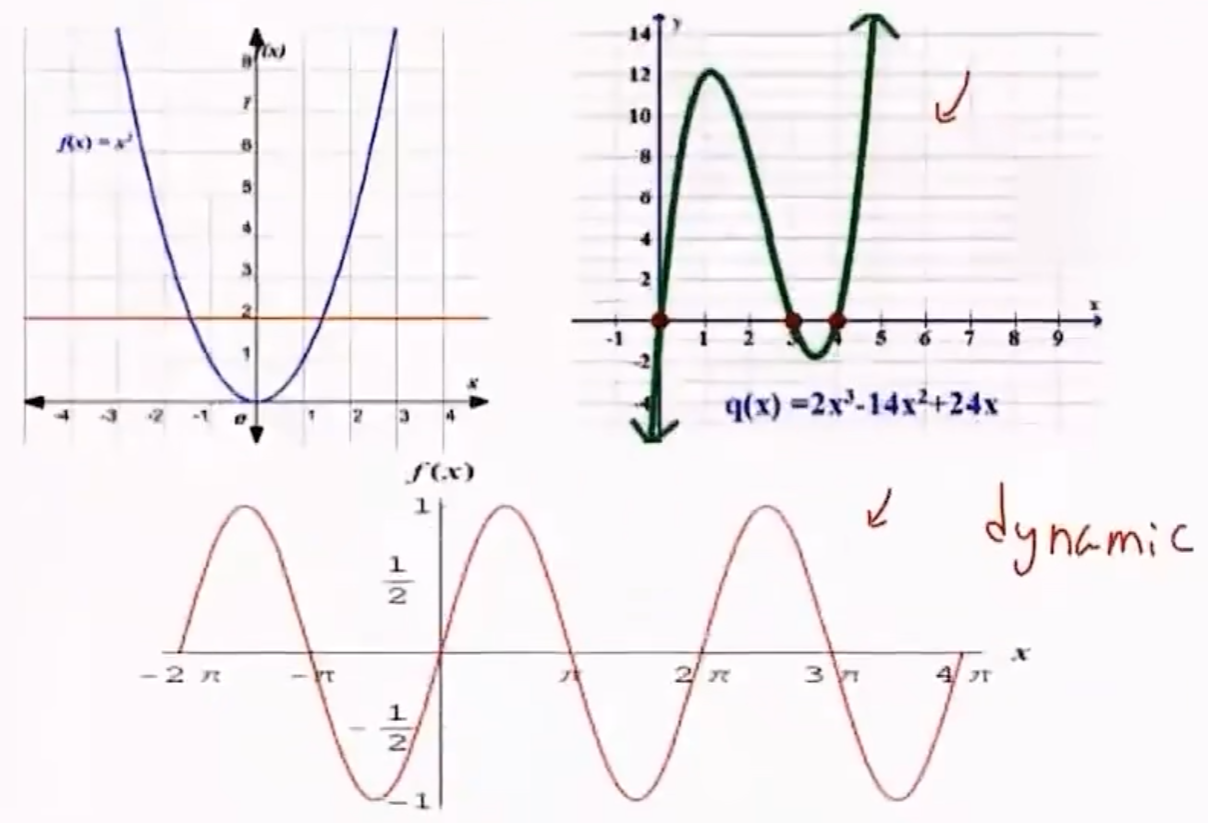
输入是否与时间有关
- 是:动态函数
- 否:静态函数
输入是否为标量
- 是:一元函数
- 否:多元函数
1.1.2 常见函数
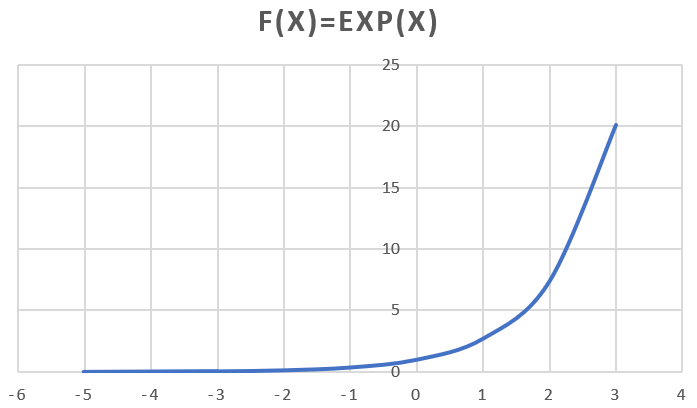
指/对数函数
$f(x)=e^x$
$f(x)=log(x)$
分段函数
原函数&反函数
原函数 $h=h(t)$ :$h=\frac{1}{2}gt^2$
反函数 $t=t(h)$ :$t=\sqrt{\frac{2h}{g}}\quad/\quad t=-\sqrt{\frac{2h}{g}}(需要附加条件,才能确定具体反函数)$
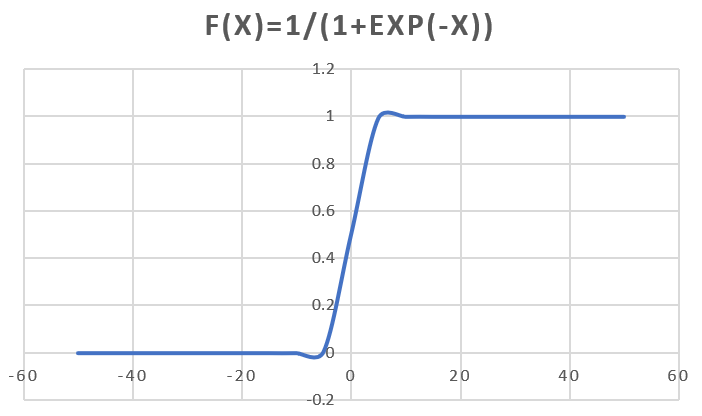
sigmod函数
$s(x)=\frac{1}{1+e^{-x}}=\frac{e^x}{e^x+1},x\in (-\infty,+\infty),y\in (0,1)$
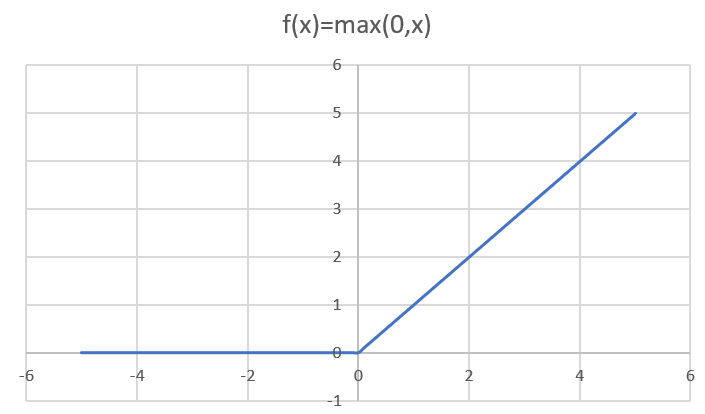
Relu函数(非负函数)
$f(x)=x^+=max\{0,x\}$
- 无梯度消失问题
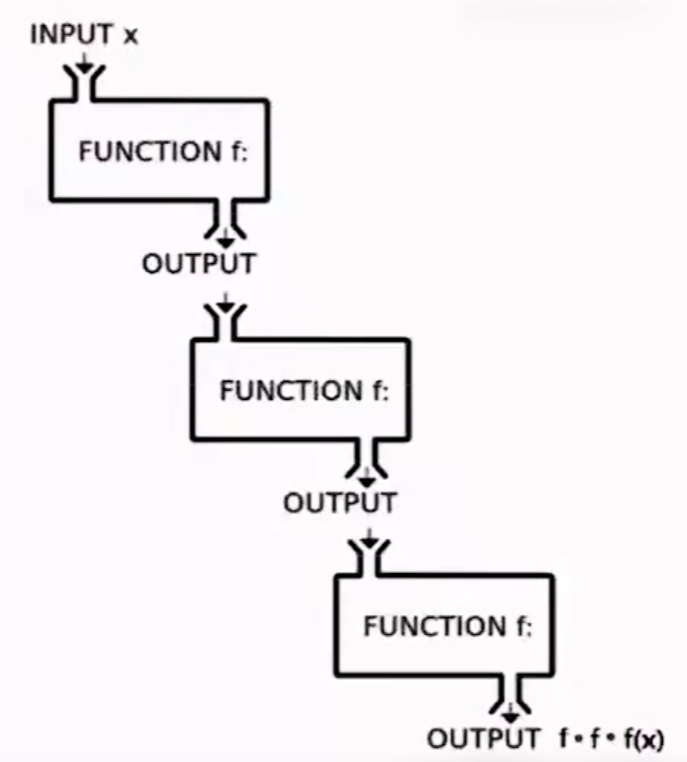
复合函数
$(g\circ f)(x)$ 表示 $g(f(x))$ ——通道
向量到张量
$\vec{a}=\left(\begin{aligned}\sigma_1\\\sigma_2\\\sigma_3\end{aligned}\right),\vec{b}=\left(\sigma_1’,\sigma_2’,\sigma_3’\right)$
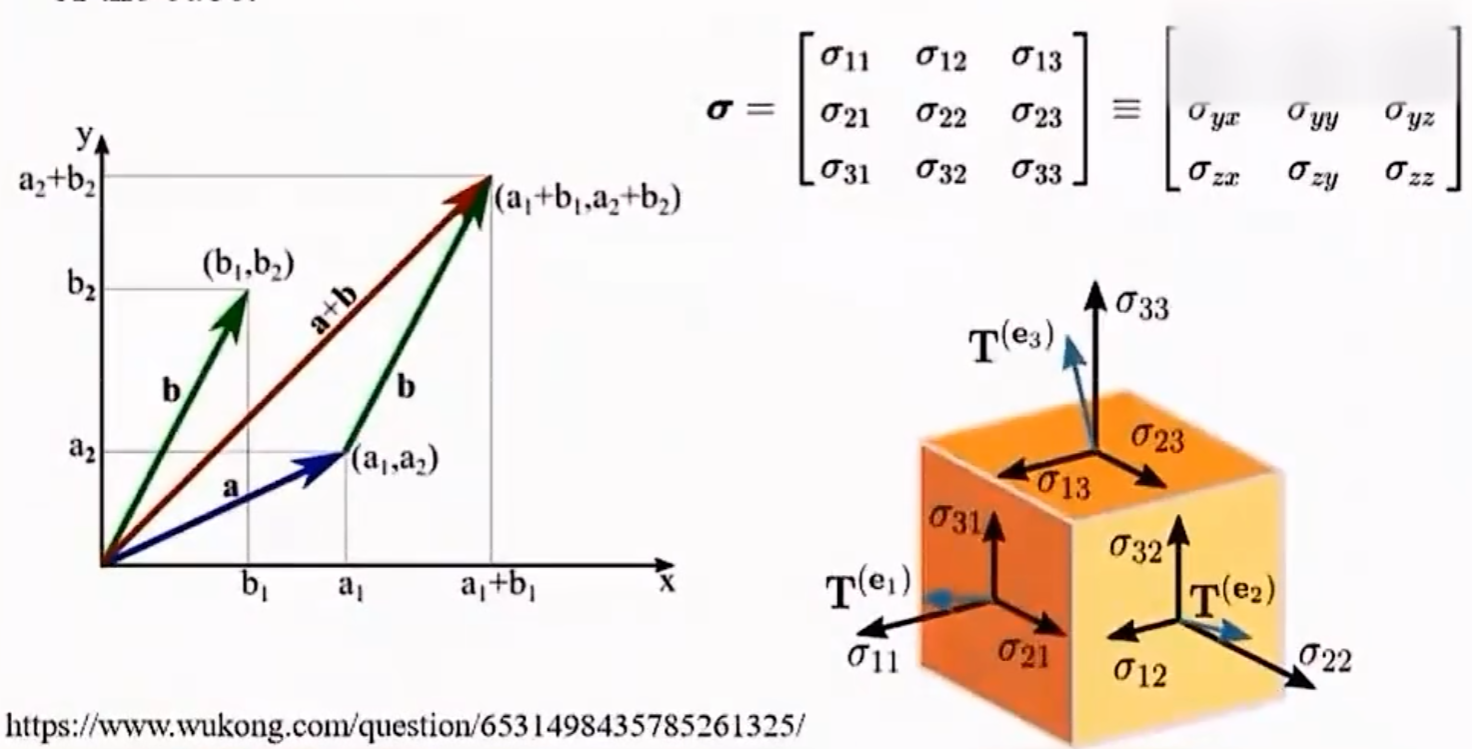
张量:
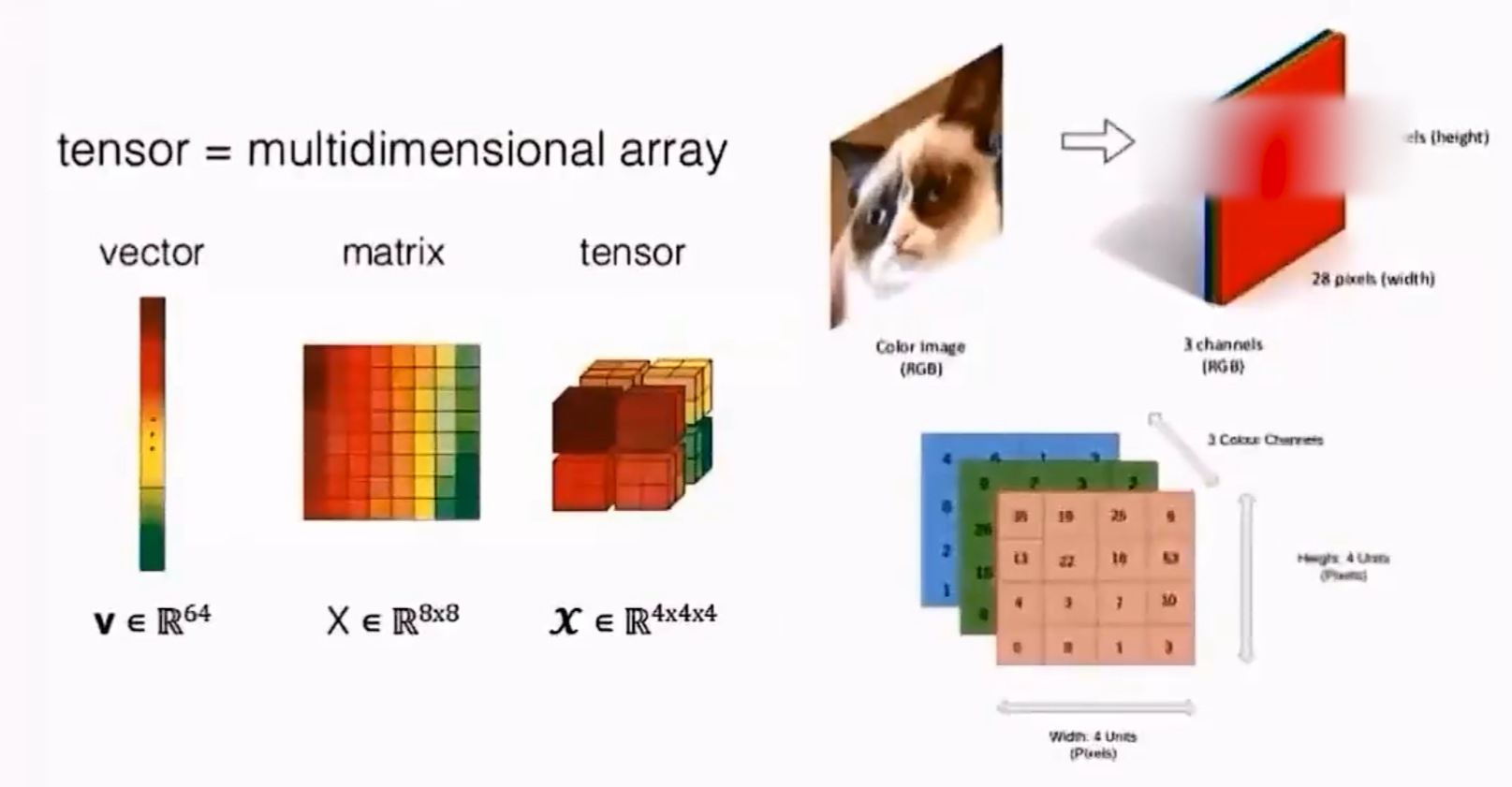
1.1.3 性质
奇偶性
- 关于y轴对称,$f(x)=f(-x)$ ,偶函数
- 关于原点对称,$f(-x)=-f(x)$,奇函数
周期性
$f(x+T)=f(x)$
单调性
1.2 极限
1.2.1 数列极限
$a_n$ 同项
等差数列:$a_n=a_1+(n-1)q$ ,$S_n=na_1+\frac{n(n-1)q}{2}$
等比数列:$a_n=a_1q$ ,$S_n=\frac{a_1-a_nq}{1-q}=\frac{a_1(1-q^n)}{1-q}$
当
数列的收敛表示为:
$\lim_\limits{n\rightarrow \infty} a_n=A$ 或 $a_n\rightarrow A(n\rightarrow \infty)$
eg:
$\lim_\limits{n\rightarrow \infty}\frac{1}{3^n}=0$ ,$\lim_\limits{n\rightarrow \infty}=\frac{n}{n+1}=1$
$\lim_\limits{n\rightarrow \infty}2^n=\infty$ 发散
1.2.2 函数极限
$\lim_\limits{x\rightarrow +\infty}e^{-x}=0$
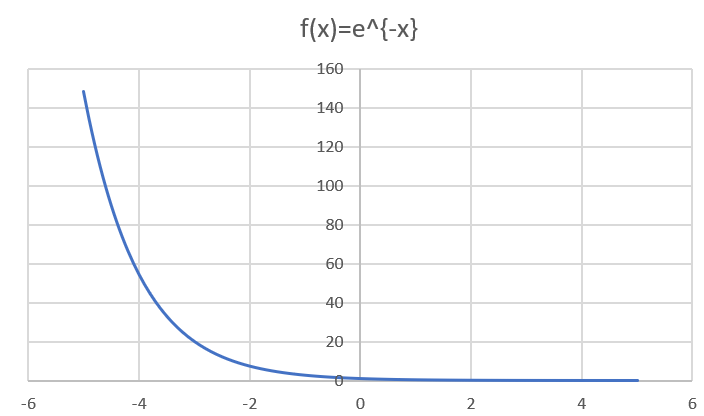
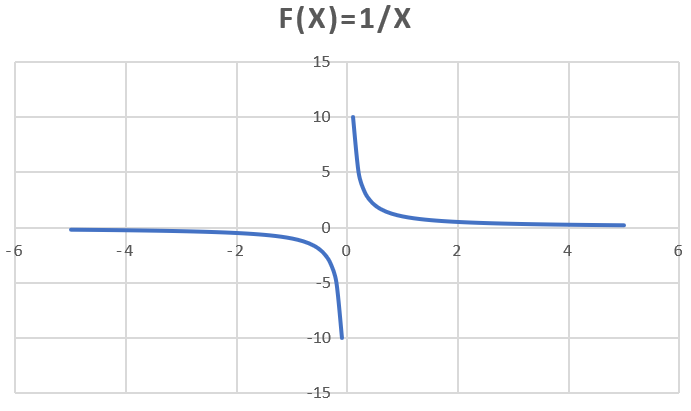
$\lim_\limits{x\rightarrow +\infty}\frac{1}{x}=0$
$\lim_\limits{x\rightarrow +\infty}arctanx=\frac{\pi}{2}$
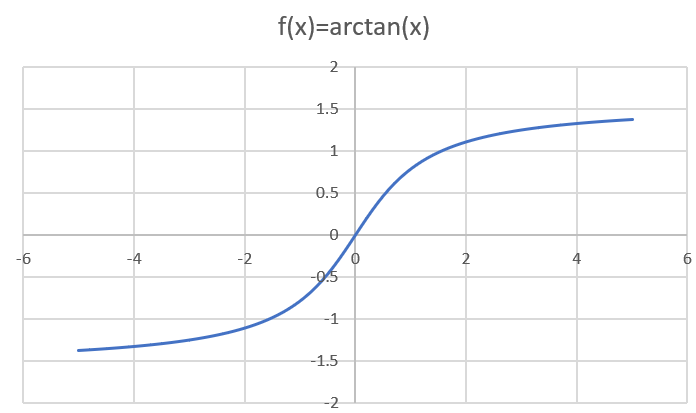
极限定义
左右极限
函数在左半邻域 $(x_0-\sigma,x_0)$,右半邻域 $(x_0,x_0+\sigma)$ 有定义
左极限:$\lim_\limits{x\rightarrow x_0^-}f(x)=A$ / $f(x)\rightarrow A(x\rightarrow x_0^-)$ / $f(x-x_0)=A$
右极限:$\lim_\limits{x\rightarrow x_0^+}f(x)=A$ / $f(x)\rightarrow A(x\rightarrow x_0^+)$ / $f(x+x_0)=A$
极限
函数在 $x_0$ 的邻域内有定义,且左极限=右极限 $\lim_\limits{x\rightarrow x_0}f(x)=A$ 或 $f(x)\rightarrow A(x\rightarrow x_0)$
充要条件:$\lim_\limits{x\rightarrow x_0^-}f(x)=\lim_\limits{x\rightarrow x_0^+}f(x)=A$
eg:
由于 $\lim_\limits{x\rightarrow 0^-}f(x)=-1\neq \lim_\limits{x\rightarrow 0^+}f(x)=1$ ,故 $\lim_\limits{x\rightarrow 0}f(x)$ 不存在
1.2.3 无穷大
表示无限增大,没有上界(收敛点)
无穷大与无穷小关系:在x的同一变换过程中, $f(x)=\infty\Rightarrow \frac{1}{f(x)}=0$
1.2.4 无穷小
以零为极限($x\rightarrow a$ 时,$\lim_\limits{x\rightarrow a}f(x)=0$)
性质 :
有限个无穷小的和、积是无穷小
无穷小个无穷小未必是无穷小
- $\lim_\limits{n\rightarrow \infty}\frac{1}{n^2}+\frac{2}{n^2}+\cdots+\frac{n}{n^2}=\lim_\limits{n\rightarrow \infty}\frac{\frac{n(n+1)}{2}}{n^2}=\frac{1}{2}$
有界变量x无穷小 $\iff$ 无穷小
无穷小的商未必无穷小
$\lim_\limits{x\rightarrow 0}\frac{x}{2x}=\frac{1}{2}$ ,$\lim_\limits{x\rightarrow 0}\frac{2x}{x^2}=\infty$
极限有无穷小的充要条件:$\lim_\limits{x\rightarrow x_0}f(x)=A\iff A+\alpha(x)$ ,$\alpha(x)$ 为 $x\rightarrow x_0$ 时的无穷小
无穷小比较
$\alpha(x),\beta(x)$ 为无穷小
- $\lim_\limits{x\rightarrow x_0}\frac{\beta(x)}{\alpha(x)}=0,\beta(x)为\alpha(x)的高阶无穷小$
- $\lim_\limits{x\rightarrow x_0}\frac{\beta(x)}{\alpha(x)}=\infty,\beta(x)为\alpha(x)的低阶无穷小$
- $\lim_\limits{x\rightarrow x_0} \frac{\beta(x)}{\alpha(x)}=C\neq 0,\beta(x)与\alpha(x)为同阶无穷小$
1.2.5 连续性
设 $f(x)$ 在x的邻域内有定义,当 $\Delta x\rightarrow0$ ,有 $\Delta y\rightarrow 0$,则 $f(x)$ 在 $x_0$ 处连续,$\lim_\limits{\Delta x\rightarrow 0}\Delta y=\lim_\limits{\Delta x\rightarrow0}(f(x+\Delta x)-f(x))=0$
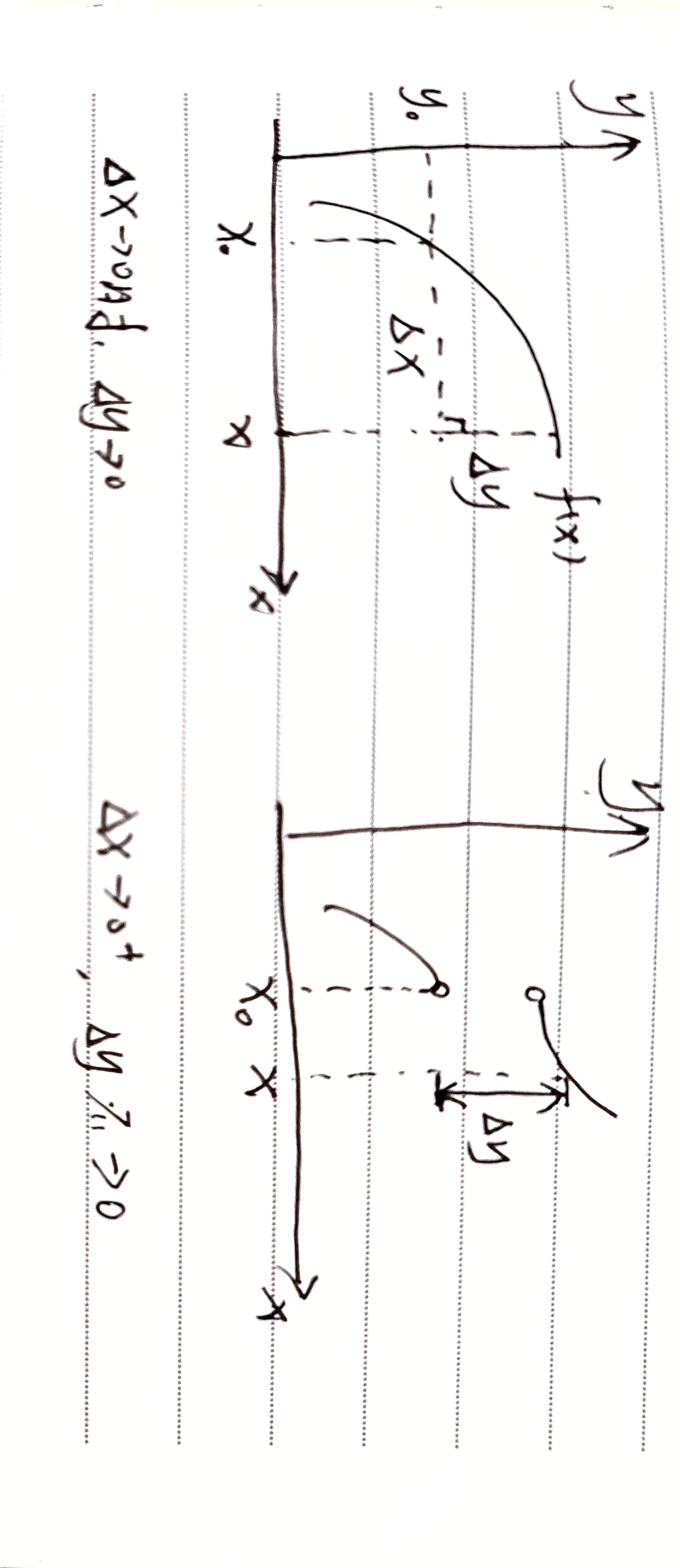
函数 $f(x)$ 在 $x_0$ 处连续,三个条件都满足 :
- 在 $x_0$ 处有定义
- $\lim_\limits{x\rightarrow x_0}f(x)$ 存在
- $\lim_\limits{x\rightarrow x_0}f(x)=f(x_0)$ 极限=函数值
1.2.6 间断点
$f(x)$ 在 $x=x_0$ 处不连续,则 $x_0$ 处为 $f(x)$ 的间断点,以下条件满足一个即为间断点
- $f(x)$ 在 $x_0$ 处无定义
- $\lim_\limits{x\rightarrow x_0}f(x)$ 不存在
- $\lim_\limits{x\rightarrow x_0}f(x)\neq f(x_0)$
分类
第一类间断点:$x\rightarrow x_0$ 时,$f(x)$ 左右极限都存在
- 跳跃间断点:$f(x_0-0)$ 与 $f(x_0+0)$ 都存在但不相同
- 可去间断点:$\lim_\limits{x\rightarrow x_0}f(x)$ 存在但 $\neq f(x_0)$
第二类间断点:至少一侧极限不存在
eg:
$f(x)=\frac{x^2-1}{x^2-3x+2}$ ,在 $x=1,2$ 处无定义,故不连续
$\lim_\limits{x\rightarrow 1^+}f(x)=\lim_\limits{x\rightarrow 1^+}\frac{x+1}{x-2}=-2$ ,$\lim_\limits{x\rightarrow 1^-}f(x)=\lim_\limits{x\rightarrow 1^-}\frac{x+1}{x-2}=-2$ ,所以 $x=1$ 为可去间断点
$\lim_\limits{x\rightarrow 2^-}f(x)=\lim_\limits{x\rightarrow 2^-}\frac{x+1}{x-2}=-\infty$ ,$\lim_\limits{x\rightarrow 2^+}f(x)=\lim_\limits{x\rightarrow 2^+}\frac{x+1}{x-2}=+\infty$ ,所以 $x=2$ 为第二类间断点
1.3 导数
表示平均变化率的极限 ,$\lim_\limits{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}=\lim_\limits{\Delta x\rightarrow 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$ ,记为 $f’(x)$
1.3.1 运算律
$(u\pm v)’=u’\pm v’$
$(\frac{u}{v})’=\frac{u’v-uv’}{v^2}(v\neq 0)$
$(uv)’=u’v+uv’$
$(cu)’=cu’$
$(\frac{c}{v})’=-\frac{cv’}{v^2}$
1.3.2 导数的几何意义
$\lim_\limits{\Delta x\rightarrow 0}\frac{\Delta y}{\Delta x}$
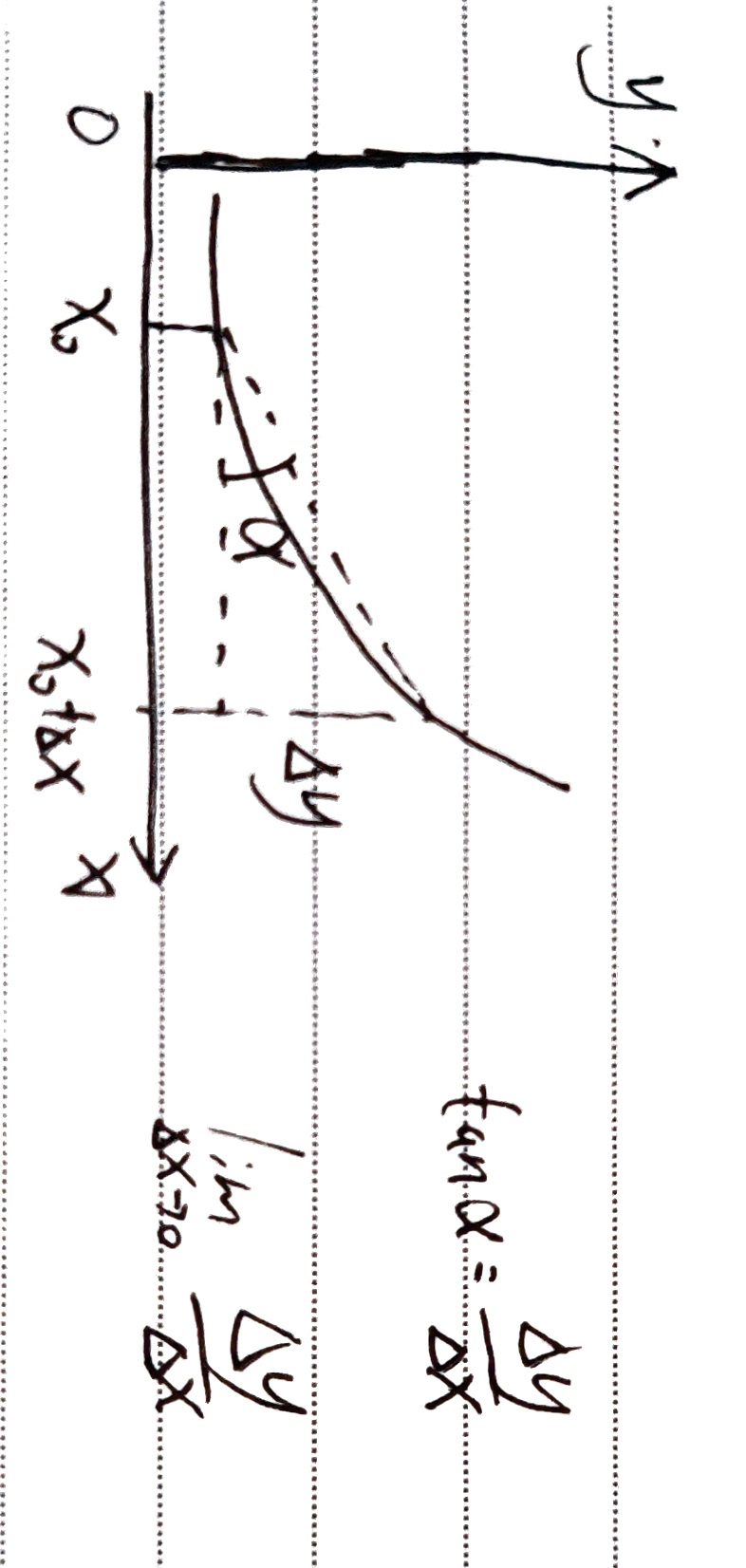
1.3.3 可微
$y=f(x)$ 在 $x_0$ 的某邻域内有定义,$x+\Delta x\in (x_0-\sigma,x_0+\sigma)$ ,若 $\Delta y=f(x_0+\Delta x)-f(x_0)$ 可表示为 $\Delta y=A\Delta x+o(x)$ ,则称 $y=f(x)$ 在 $x_0$ 处可微,记为 $dy=A\Delta x$
几何意义:
- dy:切线上纵坐标的增量
若 $y=f(x)$ 可微,则有 $\Delta y-dy=o(\Delta x)$
1.3.4 二元函数的导数
一元函数的导数:$y=f(x)$ ,$y’(x)=f’(x)$ ,只随一个变量x变化
二元函数导数:$z=f(x,y)$ ,$z=\left\{\begin{aligned}&随x变\\&随y变\\&随x,y变\end{aligned}\right.$
偏导(随一个变量变)
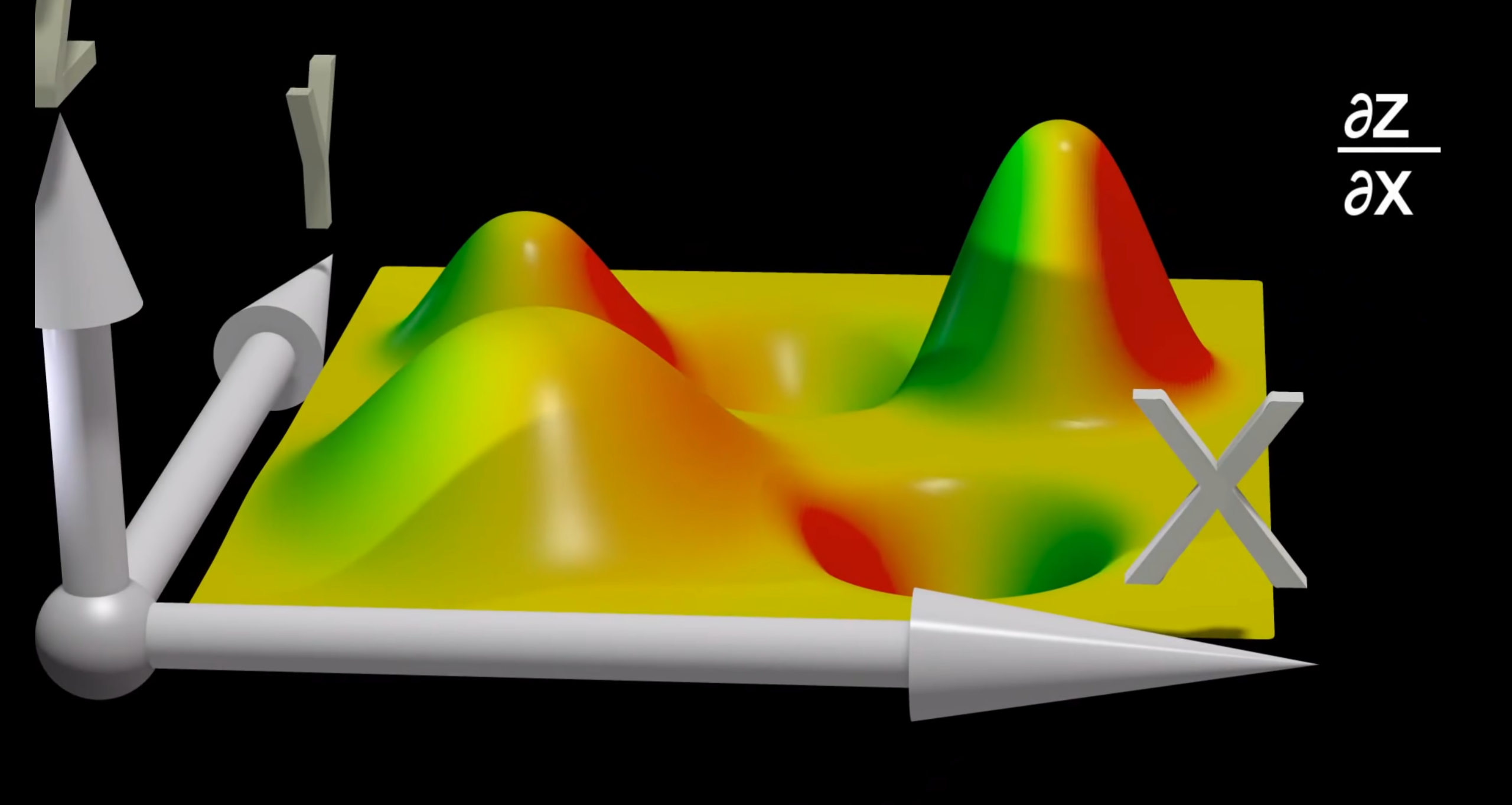
$z=f(x,y)$ 在 $(x_0,y_0)$ 的某个邻域内有定义,$y=y_0$ 时,$f(x,y_0)$ 在 $x=x_0$ 处可导,即 $\lim_\limits{\Delta x\rightarrow x_0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=A$ ,则 $z=f(x,y)$ 在 $(x_0,y_0)$ 处关于 $x$ 的偏导为 $A$ 。记为 $f_x(x_0,y_0)$ , $\frac{\partial z}{\partial x}\vert_{y=y_0,x=x_0}$
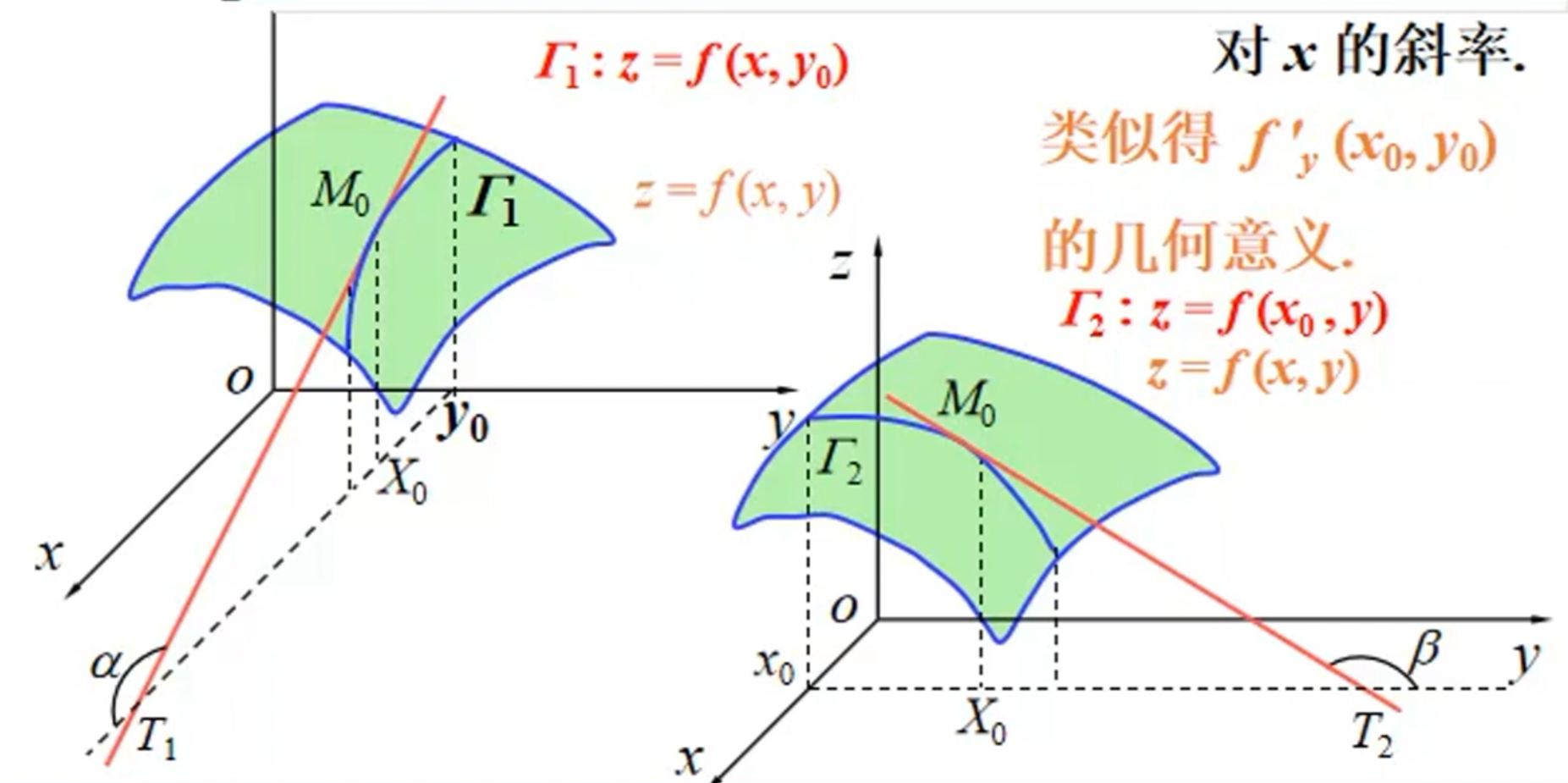
$\frac{\partial u}{\partial x}\vert_{x=x_0}$几何意义
曲线 $\Gamma:\left\{\begin{aligned}&z=f(x,y)\\&x=x_0\end{aligned}\right.$ 在 $x=x_0$ 处的切线:
- $\Gamma$ :平面 $\Pi$($x=x_0$)与 $z=f(x,y)$ 交线为 $\Gamma$
随 $y$ 的不同取值,斜率有不同取值


eg
$f(x,y)=x^2+3xy+y^2$ ,在 $(1,2)$ 处偏导,$f_x=2x+3y$ ,$f_y=3x+2y$ ,$f_x(1,2)=8$
$y(x)\vert_{y=2}=f(x,2)=x^2+6x+2,y’(x)=2x+6,y’(1)=8$
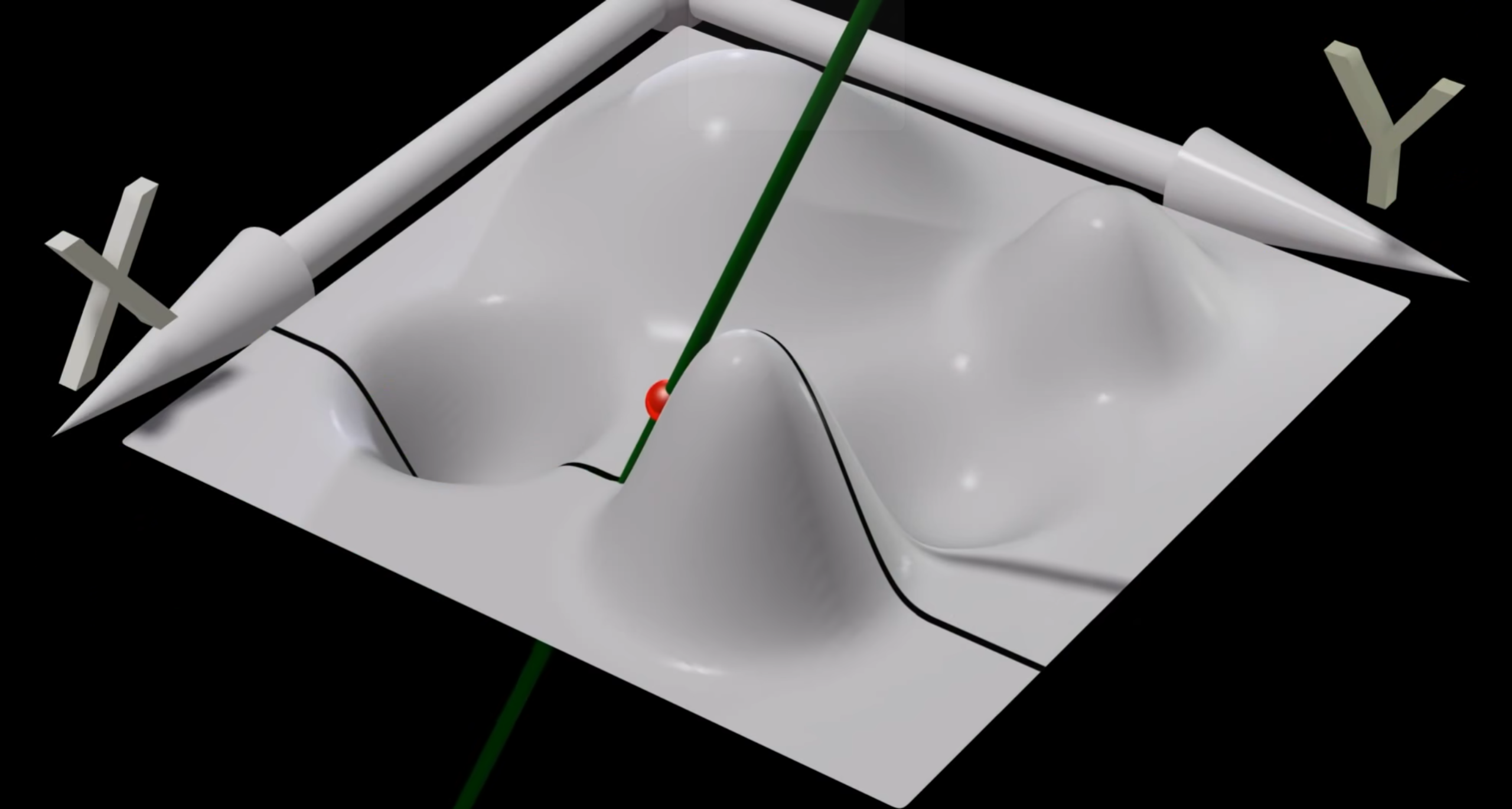
方向导(沿方向向量)
方向
$u=f(x,y,z)$ 在 $D\in R^3$ 内有定义,$R^3$ 内有一个确定点 $P_0(x_0,y_0,z_0)$ 和一个动点 $P(x,y,z)$ 确定方向向量 $\vec{l}=(a,b,c)\xRightarrow{单位化}\vec{l^0}=\left(\frac{a}{\sqrt{a^2+b^2+c^2}},\frac{b}{\sqrt{a^2+b^2+c^2}},\frac{c}{\sqrt{a^2+b^2+c^2}}\right)=(cos\alpha,cos\beta,cos\gamma)$
方向向量 $\vec{l}=\vec{P_0P}=(x-x_0,y-y_0,z-z_0)$ ,模长 $\vert \vec{l}\vert=\vert P_0P\vert=\sqrt{\Delta x^2,\Delta y^2,\Delta z^2}=t$
方向余弦
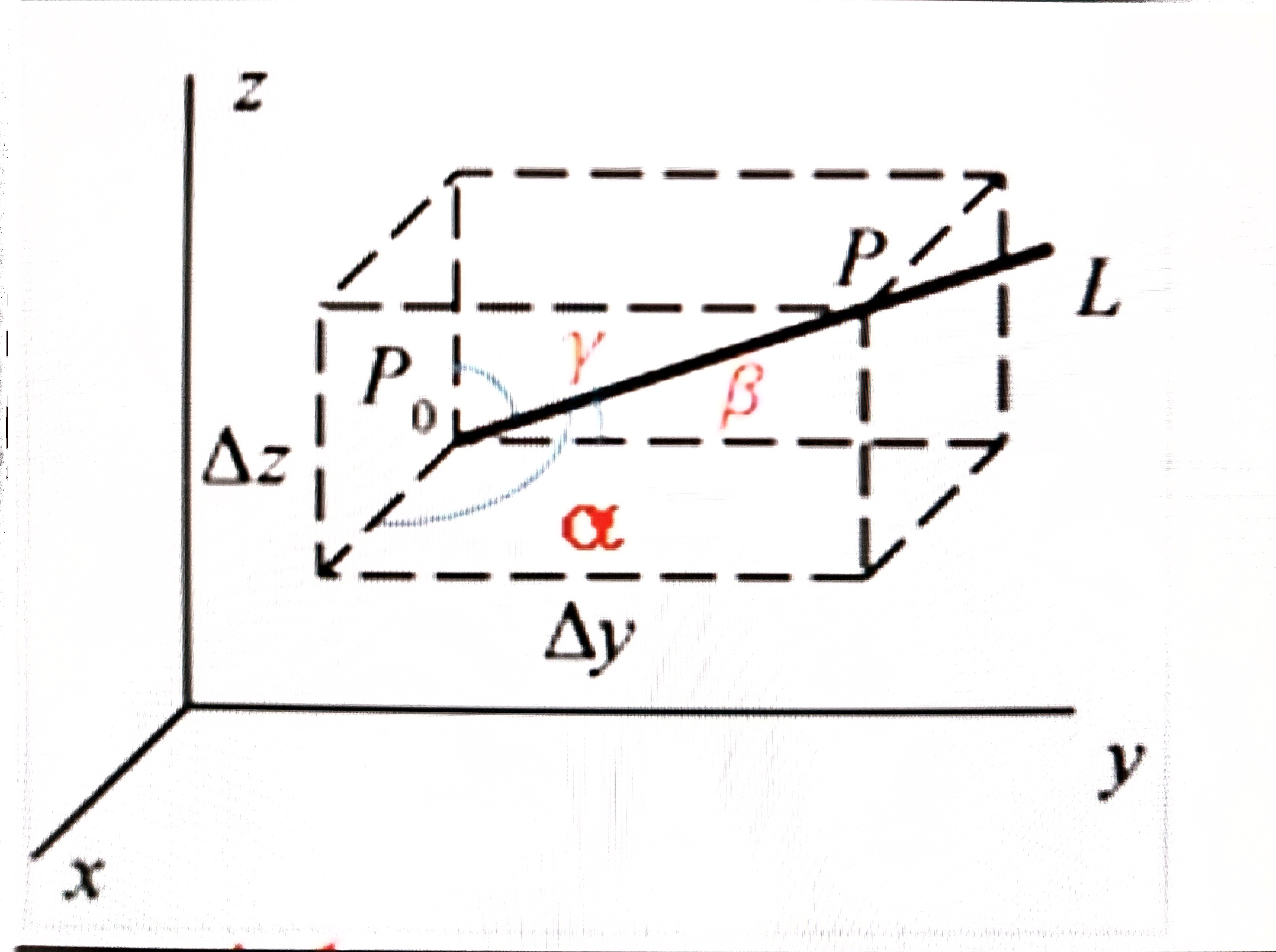
方向导
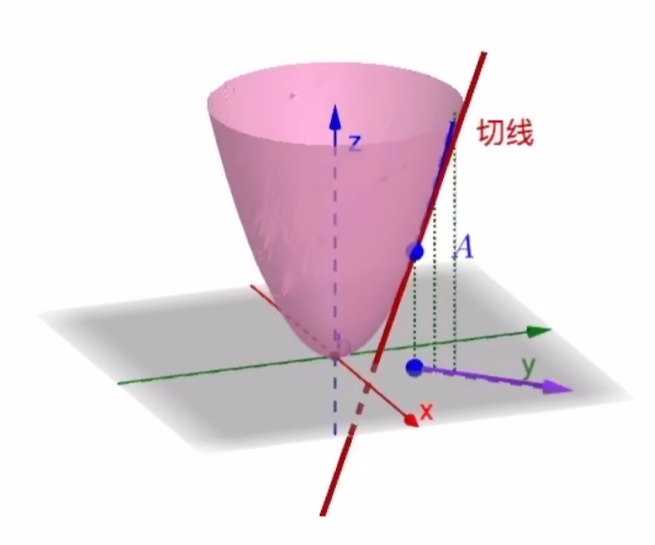
$\lim_\limits{\Delta 自变量\rightarrow 0}=\frac{\Delta 因变量}{\Delta 自变量}$
若 $\lim_\limits{\Delta l\rightarrow 0}\frac{f(x_0+\Delta lcos\alpha,y_0+\Delta lcos\beta,z_0+\Delta lcos\gamma)-f(x_0,y_0,z_0)}{\Delta l}$ 存在,则称其为 $u=f(x,y,z)$ 在 $P(x_0,y_0,z_0)$ 沿 $\vec{e_l}$ 方向的方向导数,记为 $\frac{\partial u}{\partial l}\vert_{P_0}$ ,$\frac{\partial f}{\partial l}\vert_{P_0}$
方向导几何意义
曲线 $\Gamma$ 在 $P(x_0,y_0)$ 处切线
$\Gamma$ :过方向向量 $\vec{e_l}=\left(\frac{x-x_0}{\sqrt{(x-x_0)^2+(y-y_0)^2}},\frac{y-y_0}{\sqrt{(x-x_0)^2+(y-y_0)^2}}\right)$ 做 $xoy$ 面的垂面 $\Pi$ 与 $u=f(x,y,z)$ 有交线 $\Gamma$
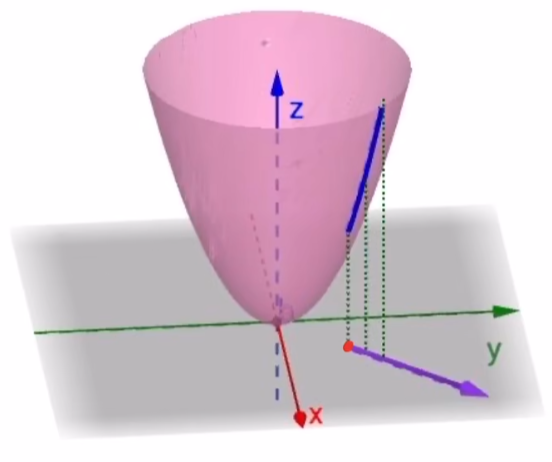
$P(x,y)$ 沿 $\vec{e_l}$ 变化,对应不同的坐标点 P,方向导为 $z=f(x,y)$ 在 $P_0$ 点切线
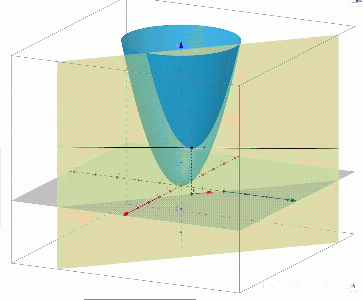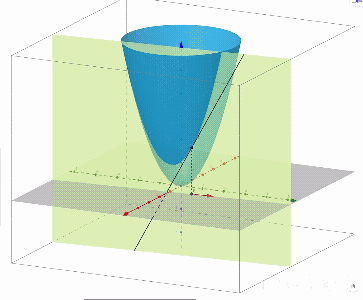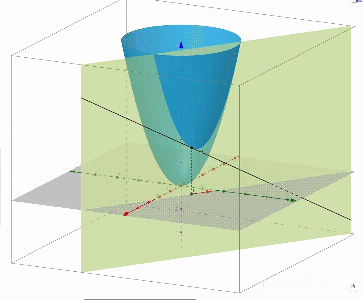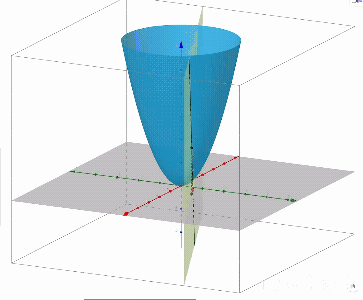
特殊方向导
沿 $x$ 轴方向 $\vec{e_l}=(1,0)$ ,$\frac{\partial f}{\partial l}=\lim_\limits{\Delta l\rightarrow 0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\sqrt{\Delta x^2}}=f_x(x_0,y_0)$
沿 $y$ 轴方向 $\vec{e_l}=(0,1)$ ,$\frac{\partial f}{\partial l}=\lim_\limits{\Delta l\rightarrow 0}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\sqrt{\Delta y^2}}=f_y(x_0,y_0)$
方向导计算
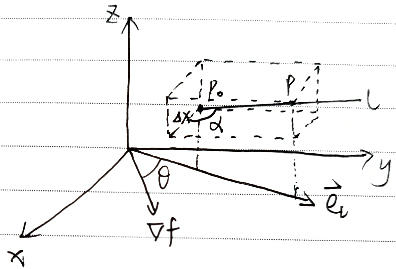
若 $u=f(x,y)$ 在 $P_0(x_0,y_0)$ 处可微,则 $f$ 在 $P_0$ 处沿任一方向导都存在,且有
eg:
求 $z=xe^{2y}$ 在 $P(1,0)$ 处沿 $P(1,0)$ 到 $Q(2,-1)$ 方向的方向导
$\vec{l}=\overrightarrow{PQ}=(1,-1)$ ,方向向量 $\vec{e_l}=\left(\frac{\sqrt{2}}{2},-\frac{\sqrt{2}}{2}\right)$ ,方向余弦 $cos\alpha=\frac{\sqrt{2}}{2},cos\beta=-\frac{\sqrt{2}}{2}$
$\frac{\partial z}{\partial l}=\frac{\partial z}{\partial x}cos\alpha+\frac{\partial z}{\partial y}cos\beta=\frac{\sqrt{2}}{2}\frac{\partial z}{\partial x}-\frac{\sqrt{2}}{2}\frac{\partial z}{\partial y}=\frac{\sqrt{2}}{2}e^{2y}-\frac{\sqrt{2}}{2}2xe^{2y}=\frac{\sqrt{2}}{2}e^{2y}(1-2x)$
在 $P(1,0)$ 的方向导为 $\frac{\partial z}{\partial l}\vert_{(1,0)}=-\frac{\sqrt{2}}{2}$
1.3.5 梯度 gradient
使方向导数最大的方向向量:
- $z=f(x,y)$ 沿梯度方向递增(假设方向向量的起点为原点)
方向导:
当 $\theta=0$ 时,有 $\frac{\partial z}{\partial l}\vert_{max}=\vert \bigtriangledown f\vert$
某一方向上的方向到为 $\Gamma$ 的切线
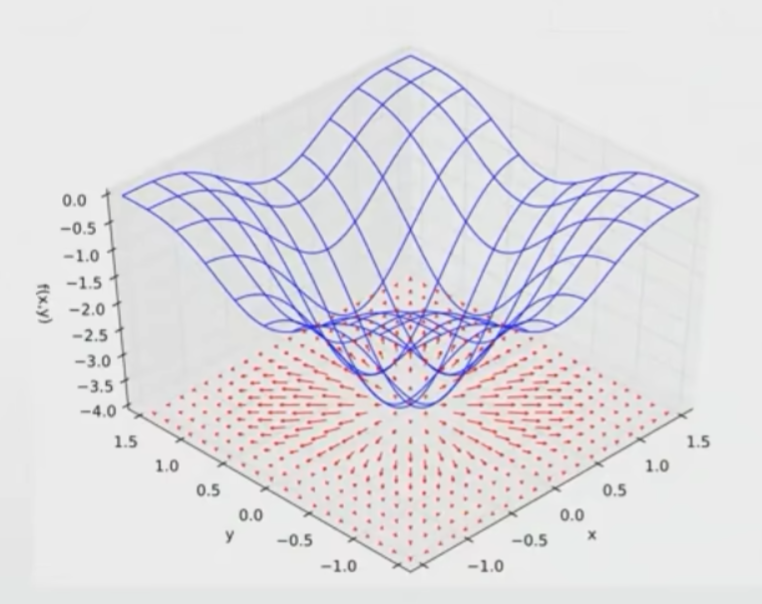
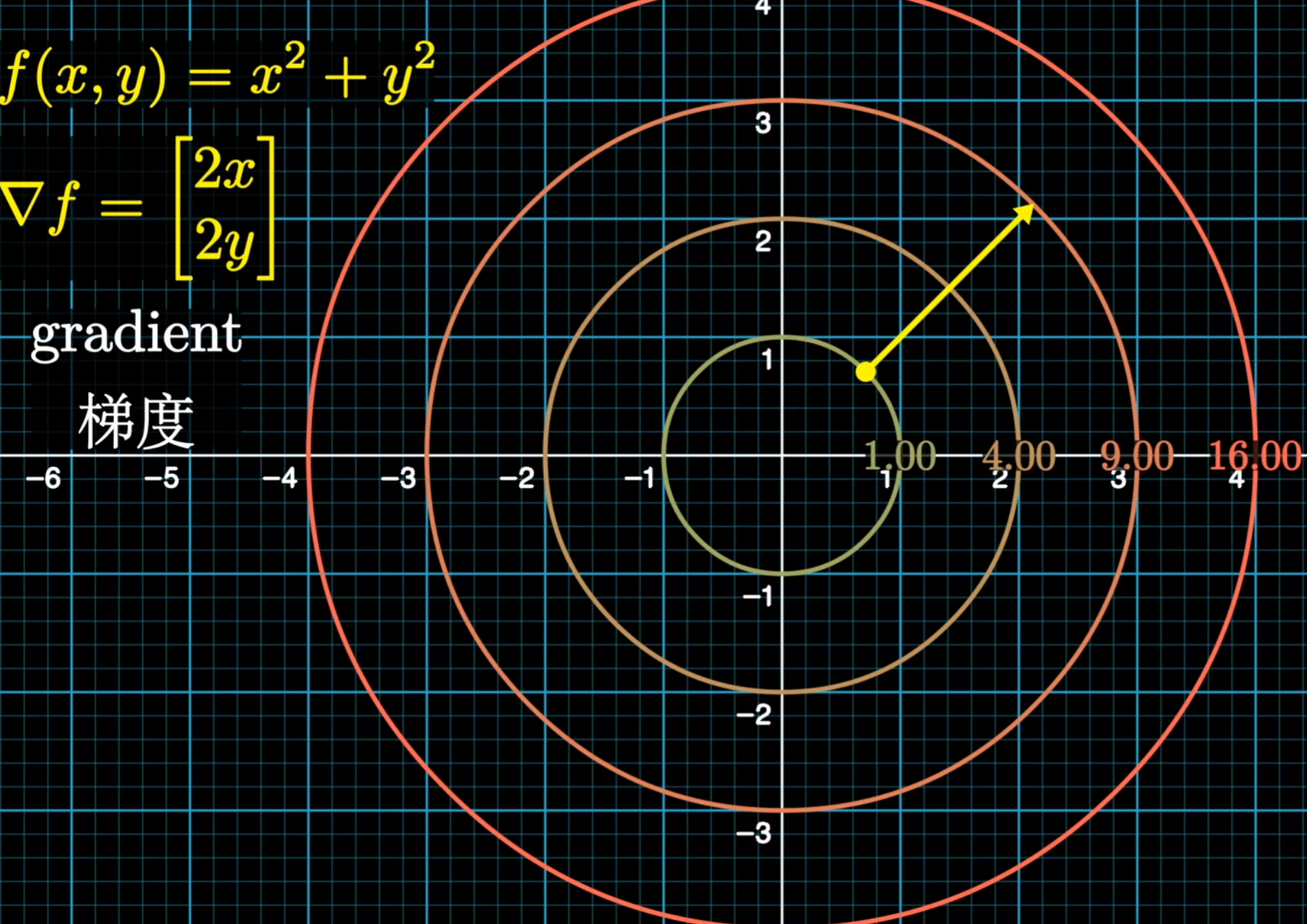
某一点沿着不同方向有不同的方向导,方向导最大的方向为梯度方向 $\bigtriangledown f\overset{\Delta}{=}(f_x’,f_y’)$ ,且为 $\vert \bigtriangledown f\vert=\sqrt{(f_x’)^2+(f_y’)^2}$
梯度方向与 $f$ 等值线垂直
如:$z=x^2+y^2$
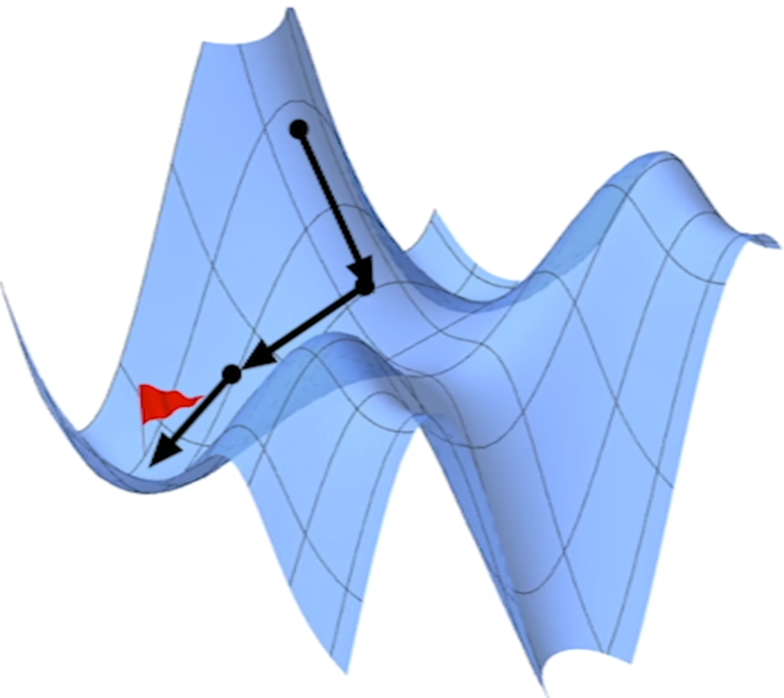
梯度下降法(方向导与极值)
找极小值:
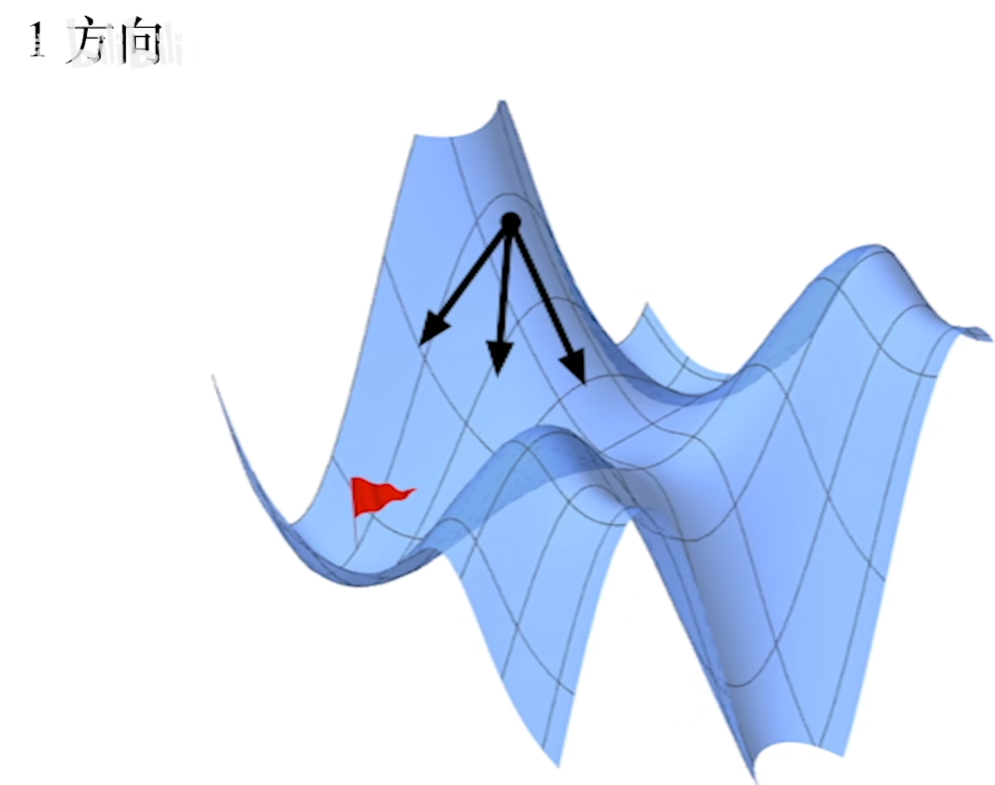
方向: $梯度反方向(-\bigtriangledown f)$
大小
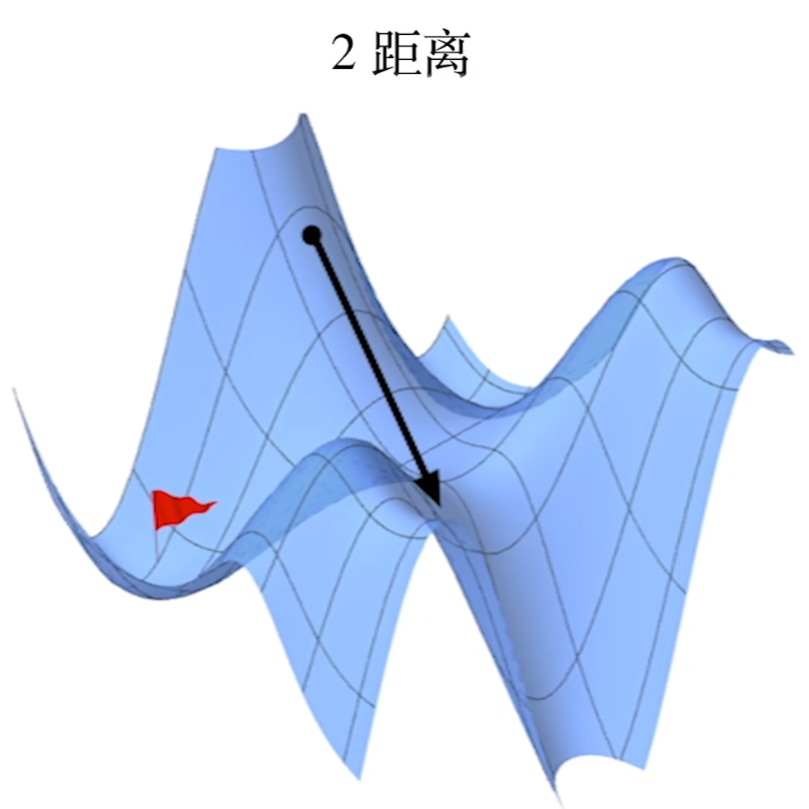
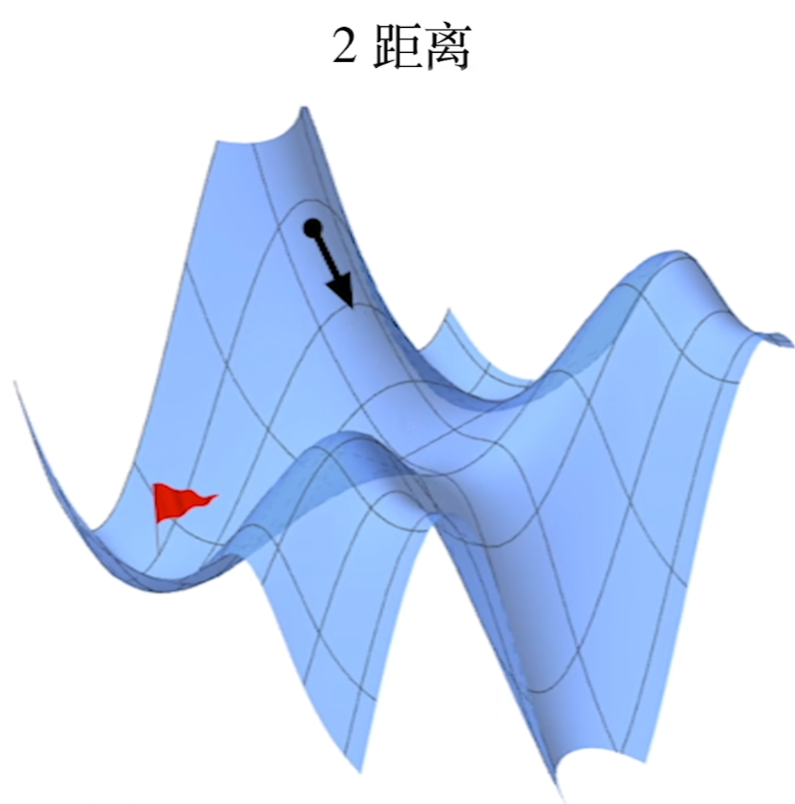
终止条件: $\vert \bigtriangledown f\vert\le \epsilon,梯度随z下降,在最低点 \vert \bigtriangledown f\vert\approx 0$
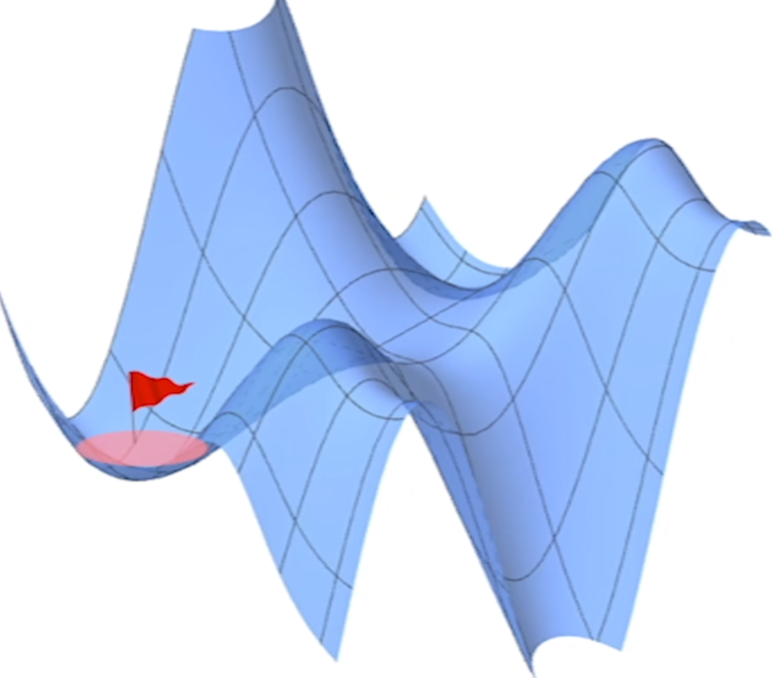
- $z=f(x,y)$ 沿梯度方向递增,沿梯度反方向递减
已知导数为沿曲线 $\Gamma$ 运动的点的切线
- 方向向量:运动方向
- 方向向量 $\vec{e_l}$ 上的点:$\Gamma$ 上的点
根据可微,$-\bigtriangledown f=\frac{\Delta f}{\vec{e_l}}\iff \frac{z_1-z_0}{\vec{e_l}}=-\bigtriangledown f\Rightarrow z_1-z_0=-\bigtriangledown f\cdot \vec{e_l}=-\bigtriangledown f\Rightarrow z_1-z_0=-\bigtriangledown f$
eg:
假设 $z=f(x,y)=x^2+y^2$ ,$z_0=f(1,2)$ 梯度 $\bigtriangledown f=\left(\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}\right)=(2x,2y)$
$z_1=z_0-\bigtriangledown f\vert_{(1,2)}=f(1,2)-f(2,4)=f(-1,-2)$
$z_2=z_1-\bigtriangledown f\vert_{(-1,-2)}=f(-1,-2)-f(-2,-4)=f(1,2)$
…
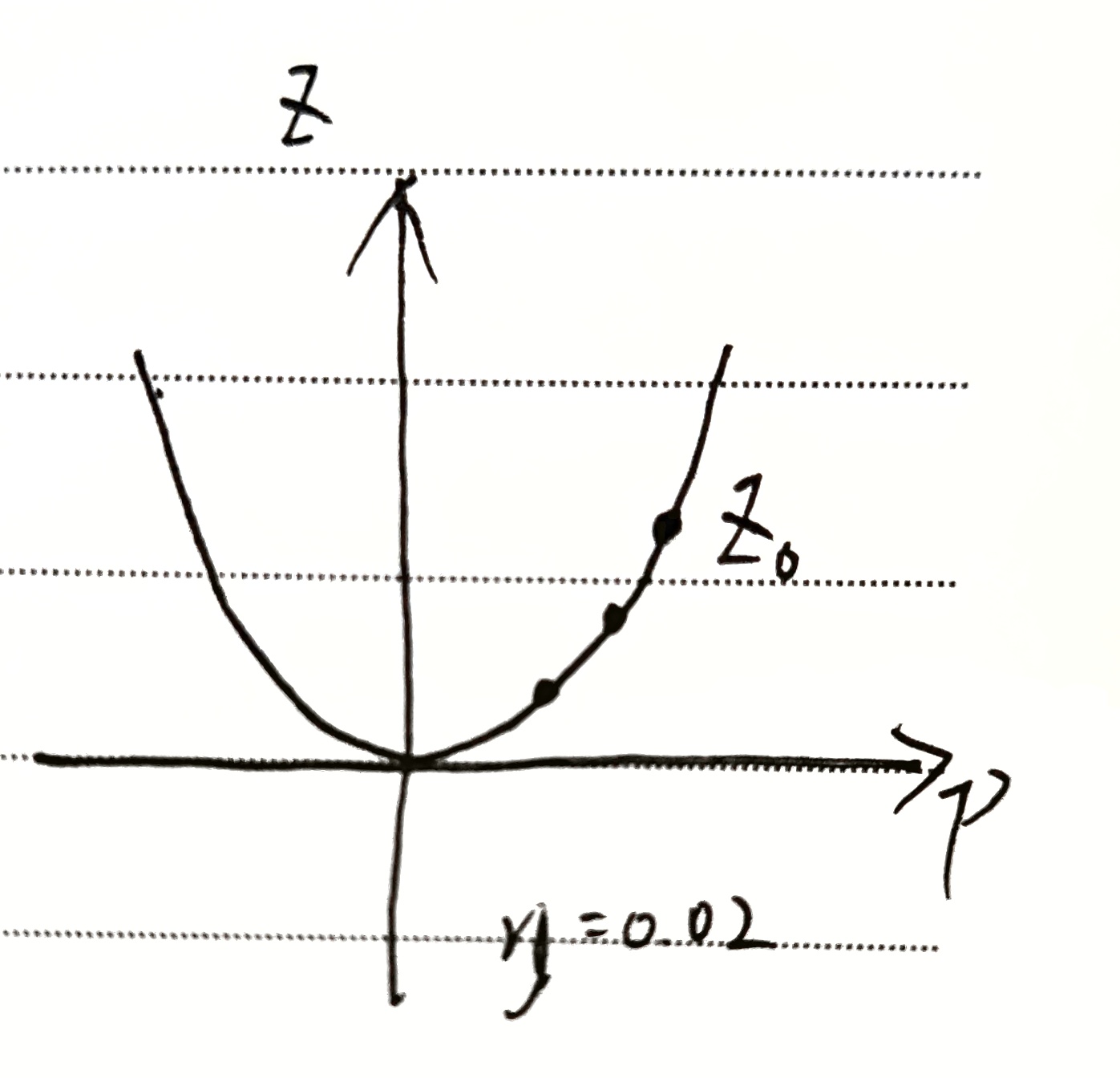
会进入循环,所以需要引入学习率 $\eta$ 来控制步长,即 $z=z’-\eta \bigtriangledown f$
$\eta > 1$ ,$z$ 上升
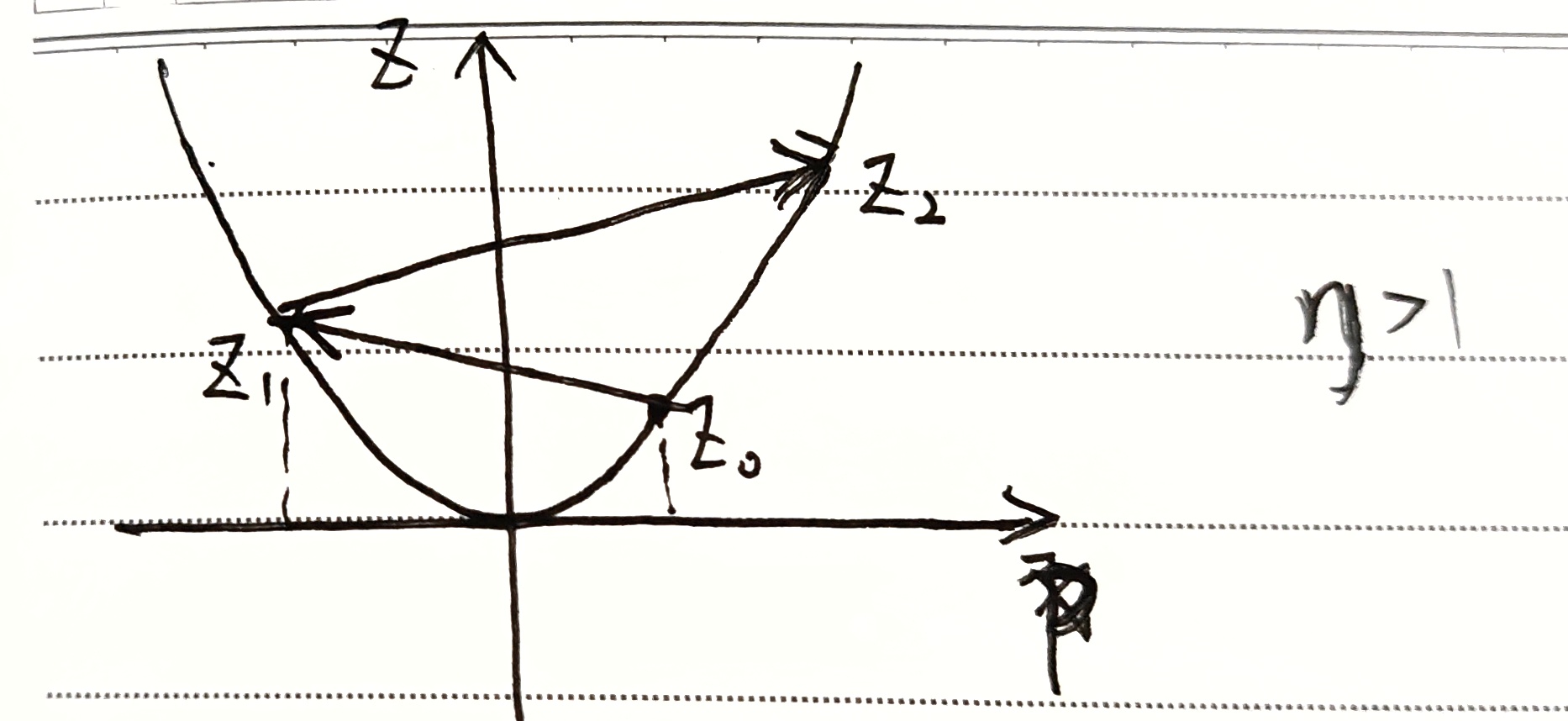
$\eta = 1$ ,$z$ 振荡
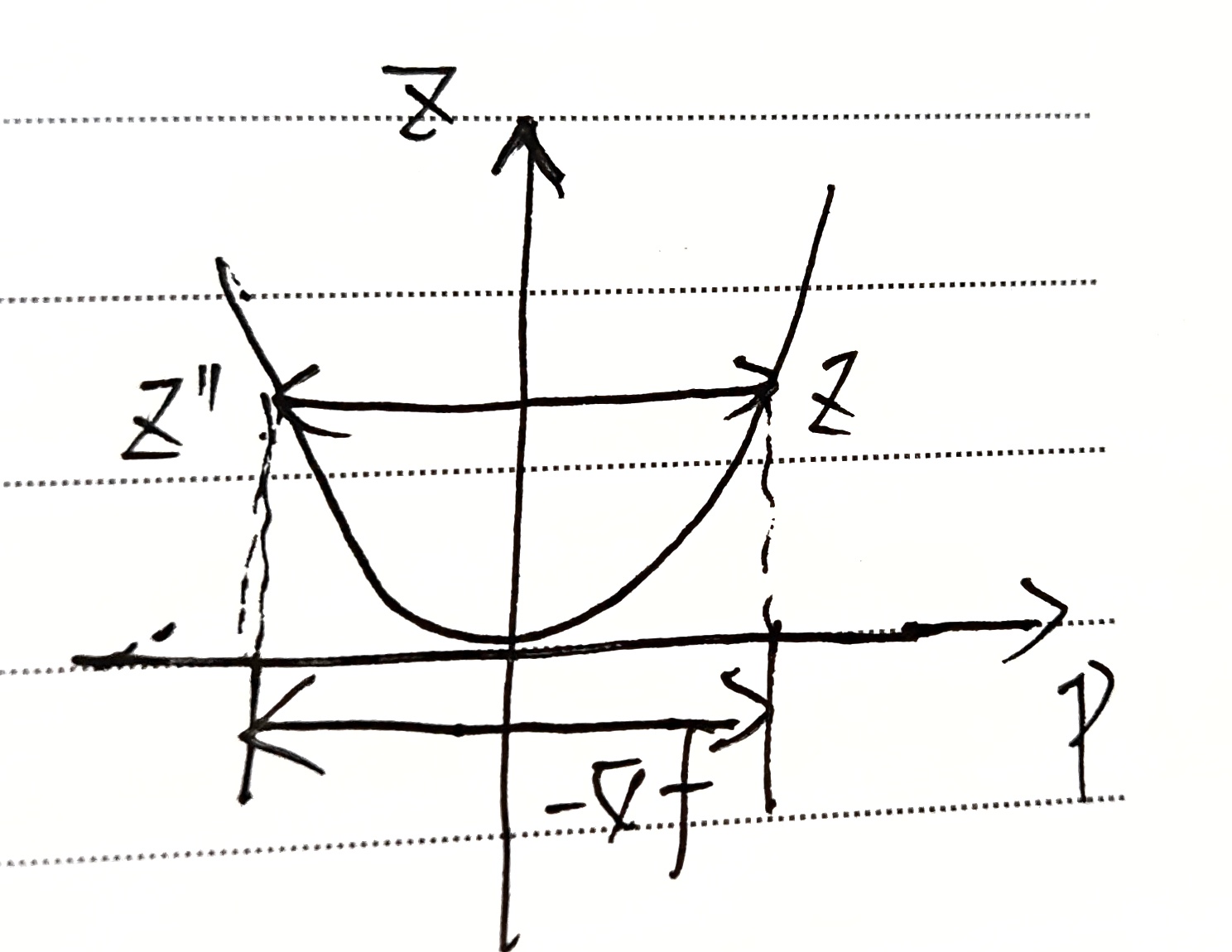
$\eta < 1$ ,$z$ 下降。且 $\eta$ 越大,下降速度越快
$\eta = 0.02$
$\eta = 0.2$
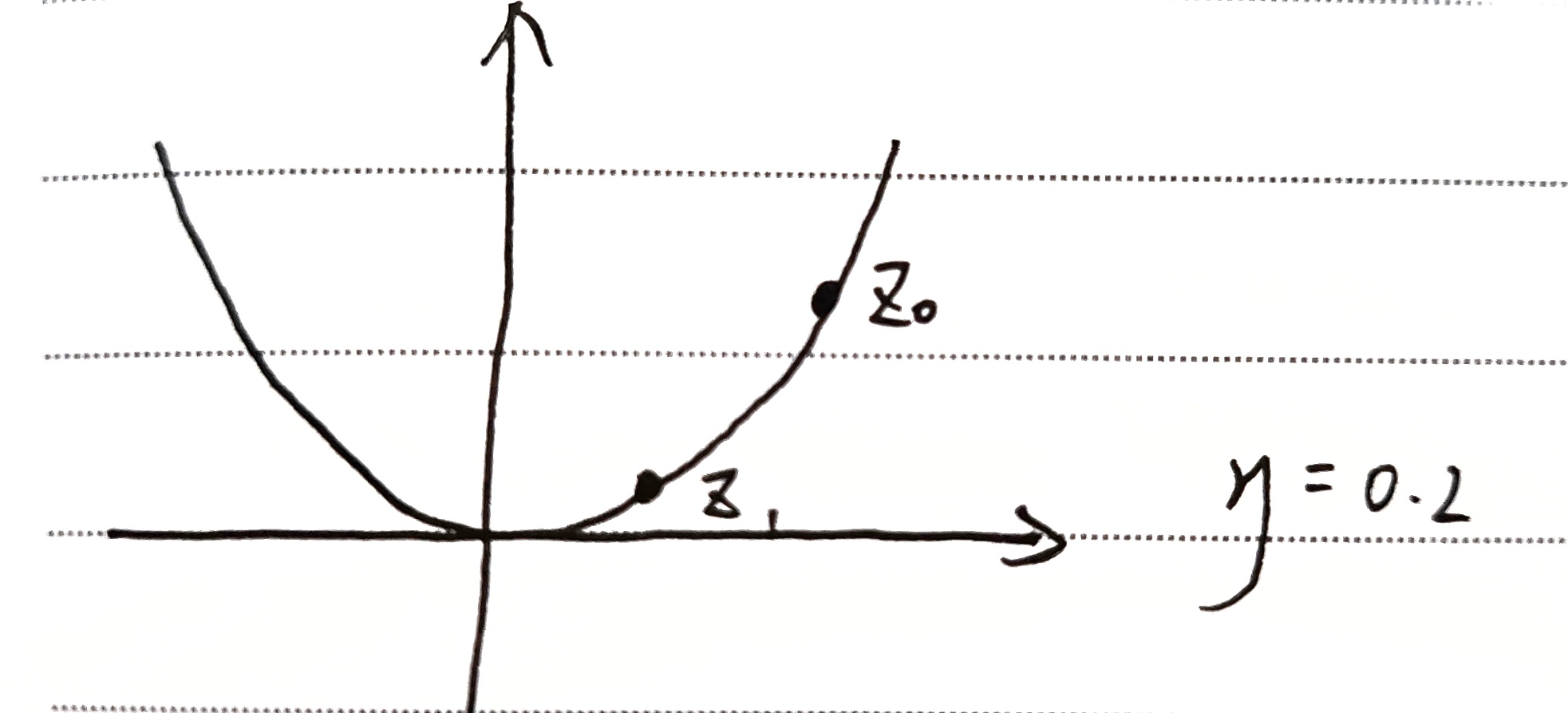
eg:
有 $u=f(x,y)=x^2+2y^2$ ,$(x_0,y_0)=(-3.5,-3.5),\eta=0.1$

1.4 微积分
用于求解速度、面积、体积等可累积量
1.4.1 基本思想
以直代曲
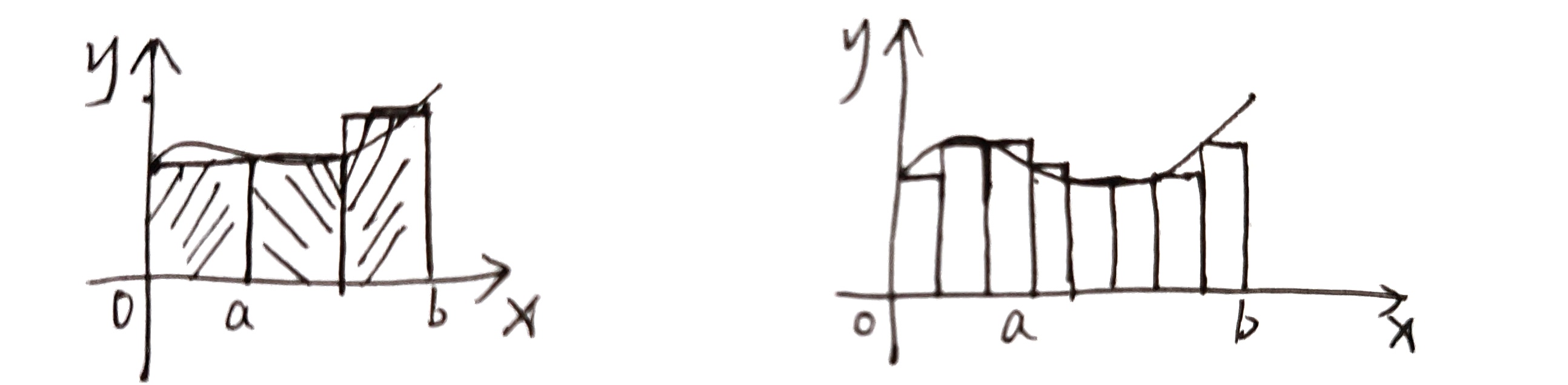
在 $[a,b]$ 间插入若干点,得到 $n$ 个小区间,每个小矩形面积 $A_i=f(\xi_i)\Delta x_i\Rightarrow A_{(a,b)}=\sum_\limits{i=1}^n f(\xi_i)\Delta x_i$
设 $\lambda$ 为小区间的最大值,$A=\lim_\limits{\lambda\rightarrow 0}\sum_\limits{i=1}^n f(\xi_i)\Delta x_i$
记为 $\int_{a}^b f(x)dx$
微分与导数关系
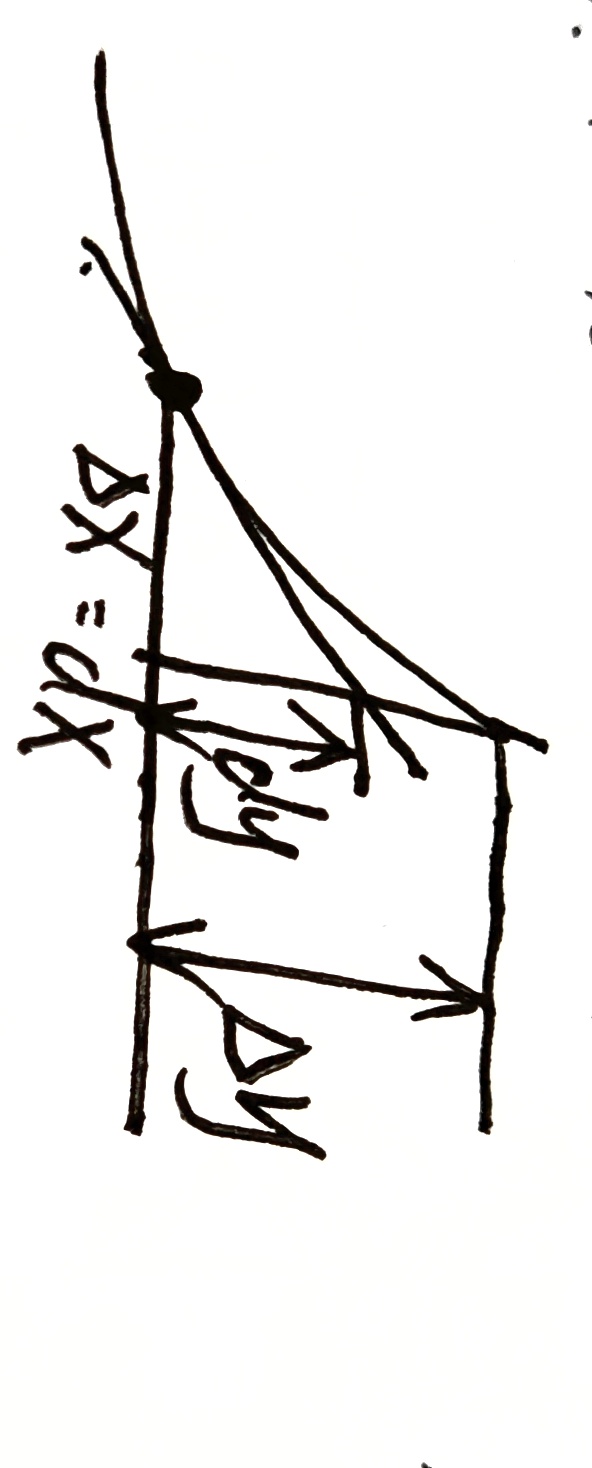
$dy$ :切线增量
$\Delta y$ :曲线增量
导数(切线斜率):$f’(x)=\frac{dy}{dx}$
$\Delta y=dy+o(\Delta x)$
1.4.2 定积分
定义
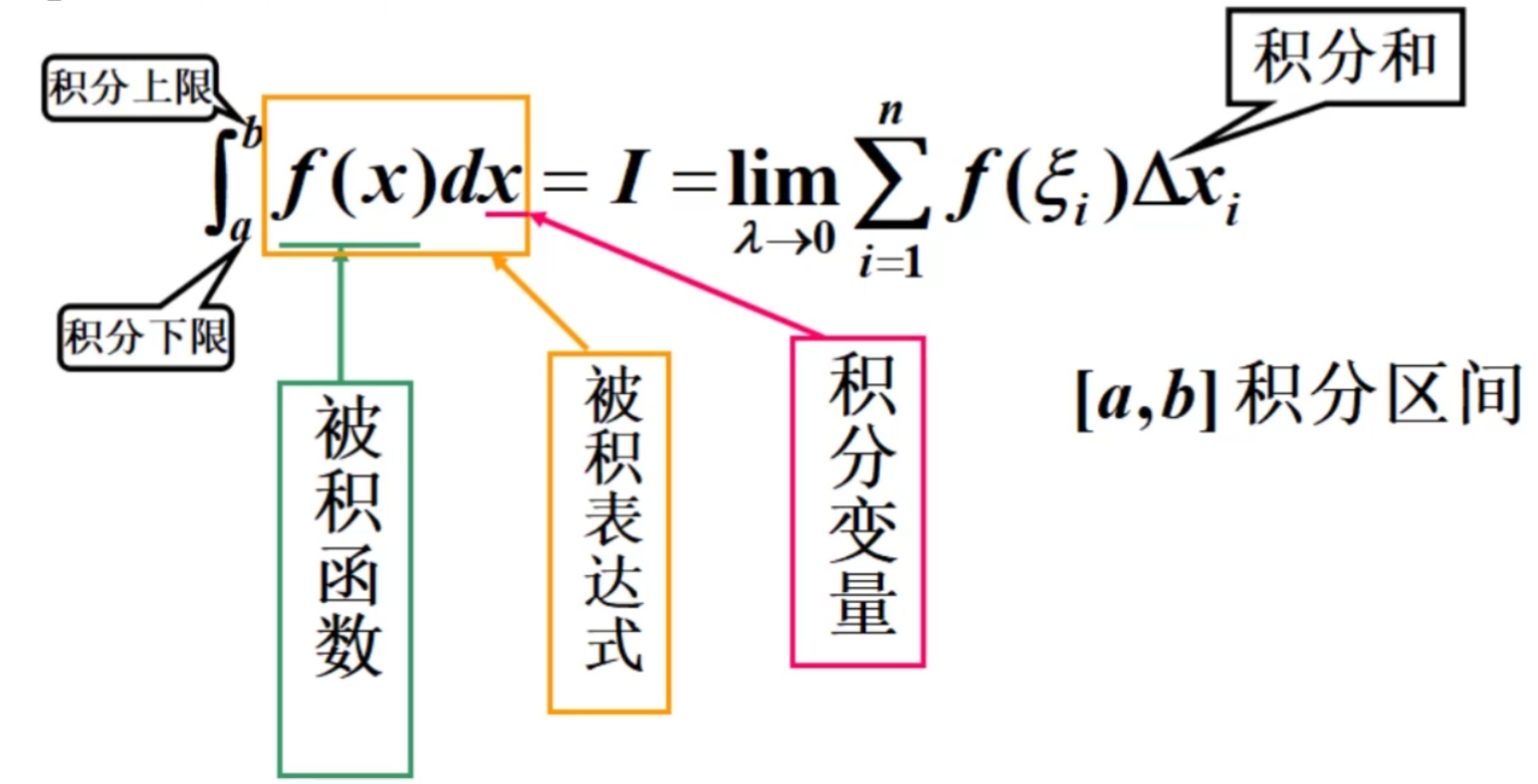
函数可积定义:$f(x)$ 在 $[a,b]$ 上的定积分存在时,则称 $f(x)$ 在 $[a,b]$ 可积
几何意义:面积A
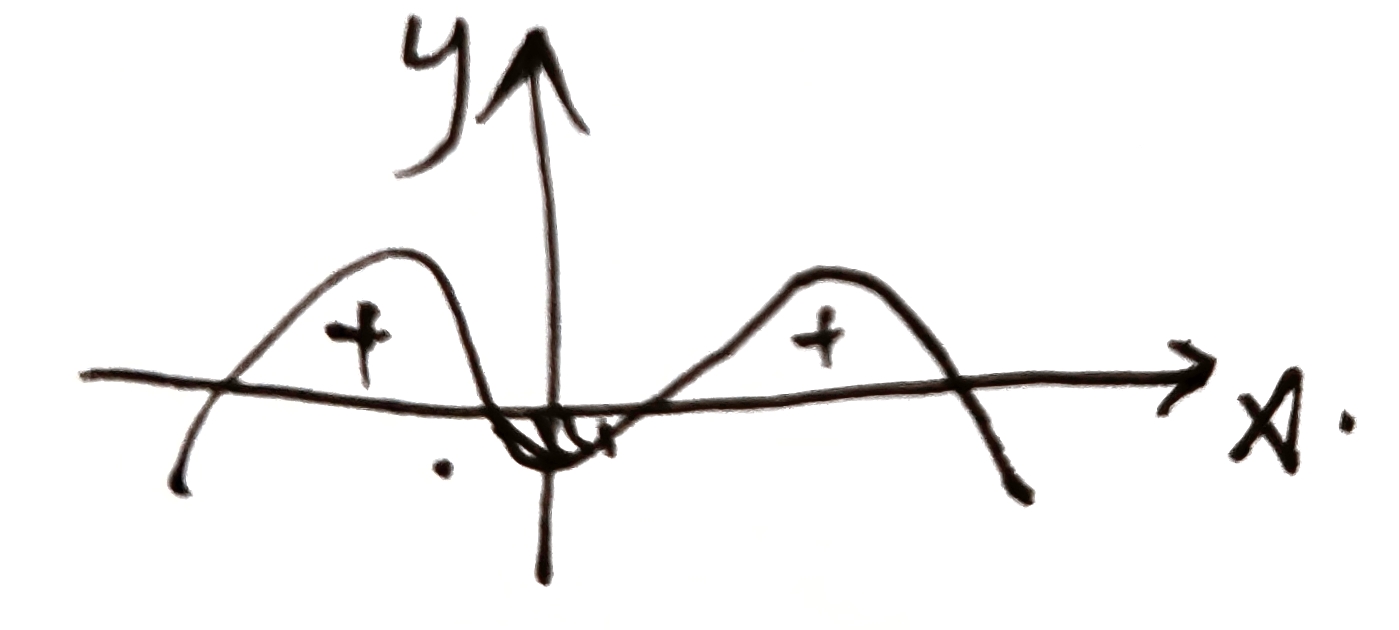
定义计算定积分
$\int_0^1x^2dx$ :将 $[0,1]$ n等分,分点为 $x_i=\frac{i}{n},(i=1,2,\cdots,n)$
小区间 $[x_{i-1},x_i]$ 的长度 $\Delta x_i=\frac{1}{n},(i=1,2,\cdots,n)$
取 $\xi_i=x_i$ ,$\sum_\limits{i=1}^n f(\xi_i)\Delta x_i=\sum_\limits{i=1}^n\xi_i^2\Delta x_i=\sum_\limits{i=1}^n(\frac{i}{n})^2\frac{1}{n}=\frac{1}{n^3}\sum_\limits{i=1}^ni^2=\frac{1}{n^3}\frac{n(n+1)(2n+1)}{6}$
$\vert \Delta x\vert\rightarrow 0\Rightarrow n\rightarrow \infty$ ,$\lim_\limits{n\rightarrow \infty}\frac{(n+1)(2n+1)}{6n^2}=\frac{1}{3}\Rightarrow \int_0^1x^2dx=\sum_\limits{i=1}^nf(\xi_i)\Delta x_i=\frac{1}{3}$
定积分性质
$\int_{a}^b[f(x)\pm g(x)]dx=\int_a^bf(x)dx\pm \int_a^bg(x)dx$
$\int_a^bkf(x)dx=k\int_a^bf(x)dx,(k为常数)$
$\int_a^b{f(x)}dx=\int_a^cf(x)dx+\int_c^bf(x)dx$
若 $[a,b]$ 上,$f(x)\ge 0\Rightarrow \int_a^bf(x)dx\ge 0,(a<b)$
定理
积分第一中值定理:$f(x)$ 在 $[a,b]$ 上连续,则在 $[a,b]$ 上至少存在一点 $\xi$ ,使 $\int_a^b f(x)dx=f(\xi)(b-a)$
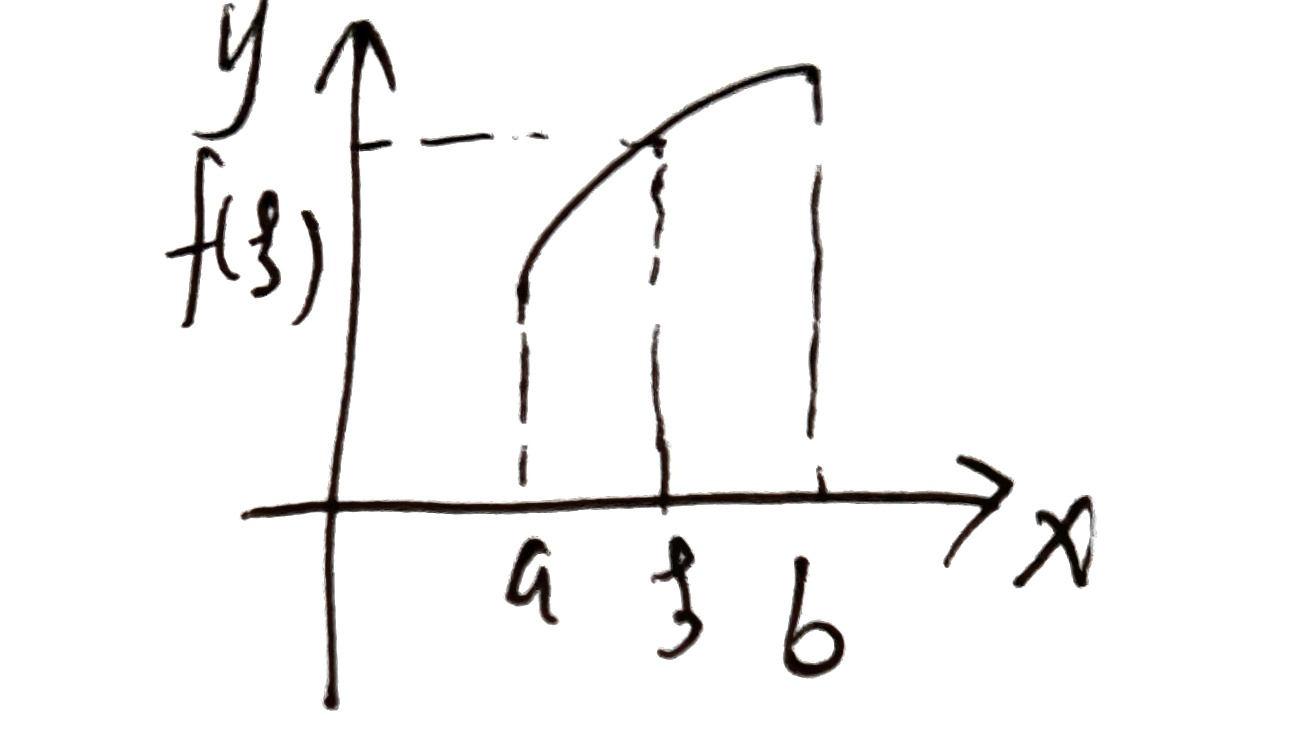
积分上限函数:$f(x)$ 在 $[a,b]$ 上连续,对于定积分 $\int_a^x f(x)dx$ 每个取值 $f(x)$ 有一个值 $\Phi(x)=\int_a^x f(t)dt$
N-L公式
$F(x)$ 连续且未 $f(x)$ 在 $[a,b]$ 上原函数,$\int_{a}^bf(x)dx =F(b)-F(a)$
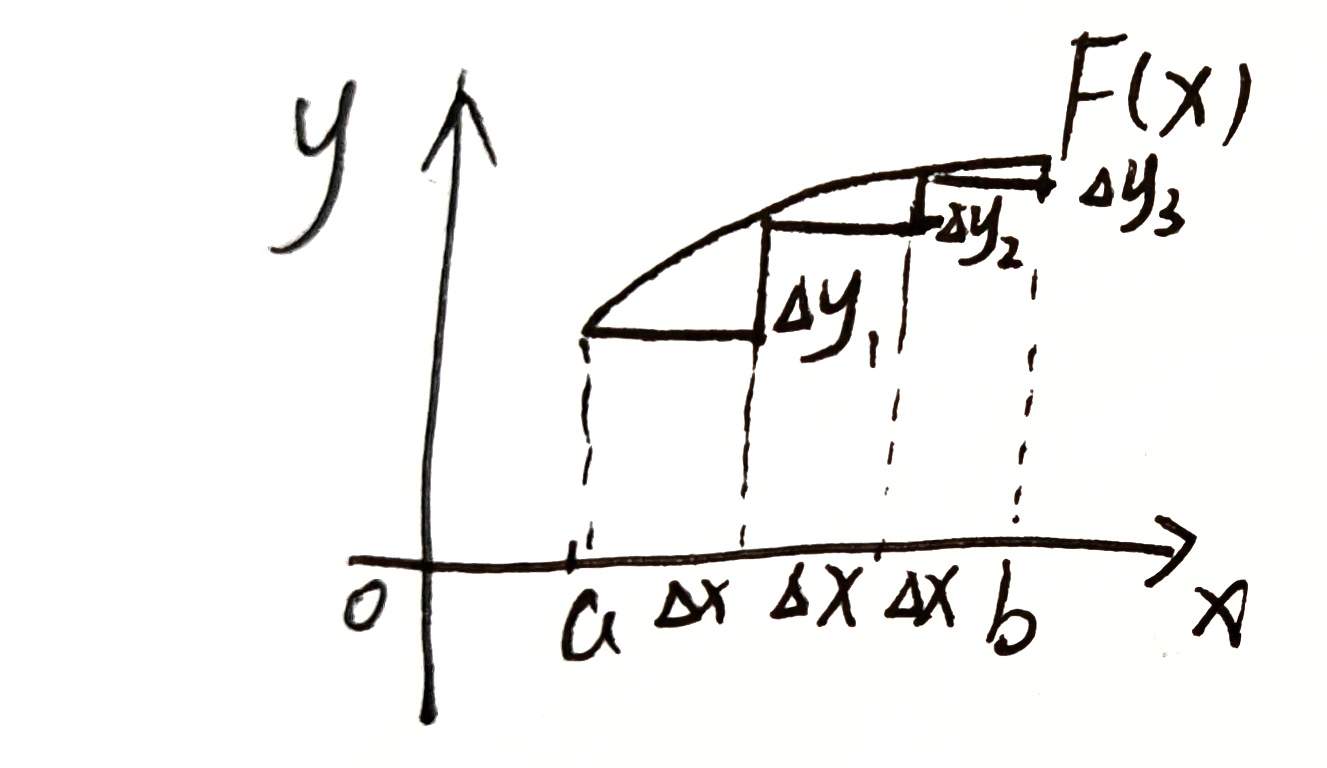
几何意义:
$F(b)-F(a)=\sum\Delta y_i$
当 $\Delta x\rightarrow 0$ 时,有 $dy_i\approx \Delta y_i,F’(x)=\frac{dF(x)}{dx}=\frac{dy}{dx}$
$\therefore\quad F(b)-F(a)=\sum\Delta y_i=\sum dy_i=\sum f(x)dx=\int_a^bf(x)dx$
基本公式
$\underbrace{\int_{a}^bf(x)dx=f(\xi)(b-a)}_{积分中值定理}=\underbrace{F’(\xi)(b-a)}_{微分中值定理}=F(b)-F(a)$
泰勒公式
以直代曲:多项式代替原函数
常用泰勒公式
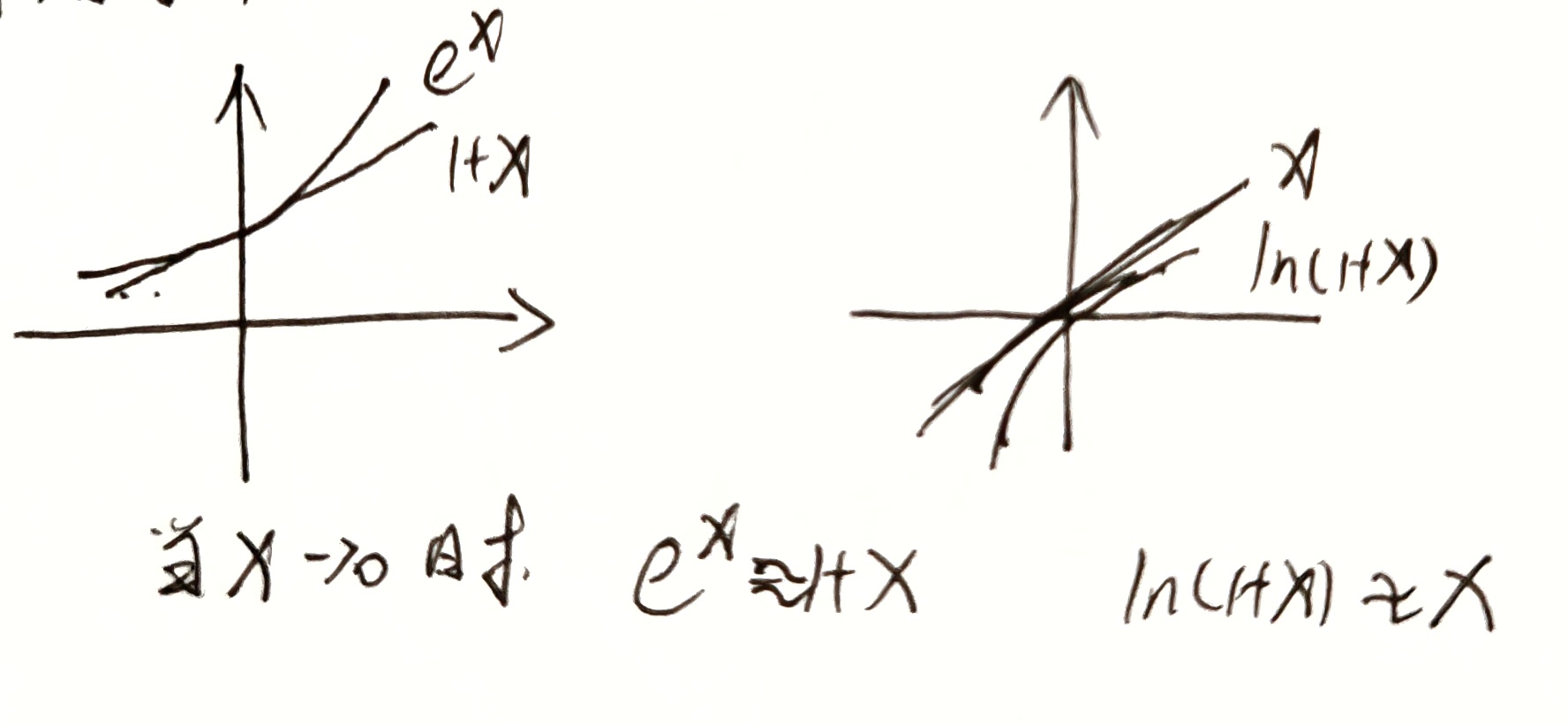
当 $x\rightarrow 0$ 时,$e^x\approx 1+x$ ,$ln(1+x)\approx x$
$P_n(x)=f(x_0)+f’(x_0)(x-x_0)+f’’(x_0)\frac{(x-x_0)^2}{2!}+f’’’(x_0)\frac{(x-x_0)^3}{3!}+\cdots+f^{(n)}(x_0)\frac{(x-x_0)^n}{n!}$
导数作用
一阶导作用:确定上升/下降趋势
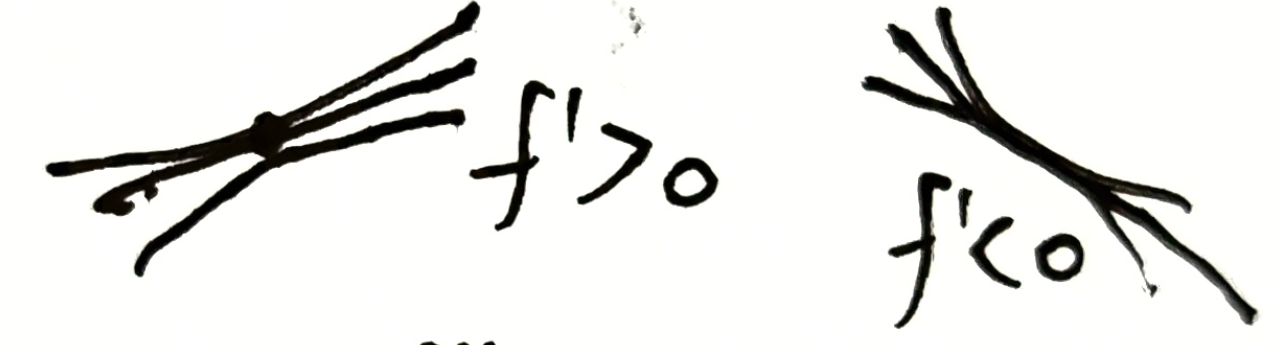
二阶导作用:确定弯曲方向(凹凸性)
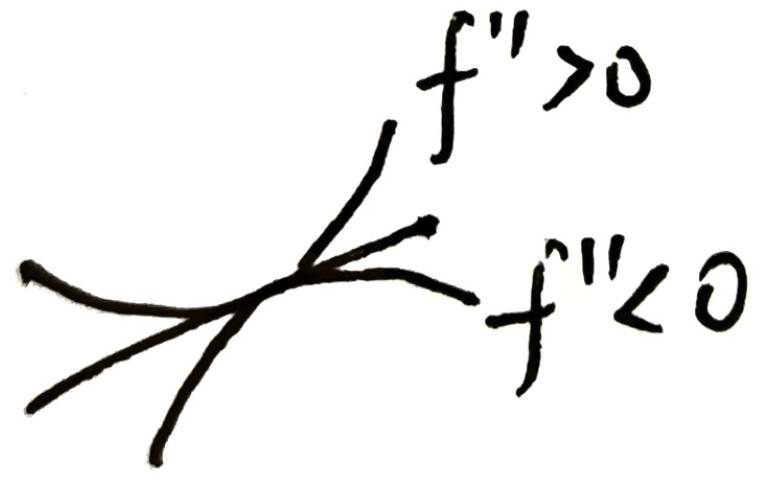
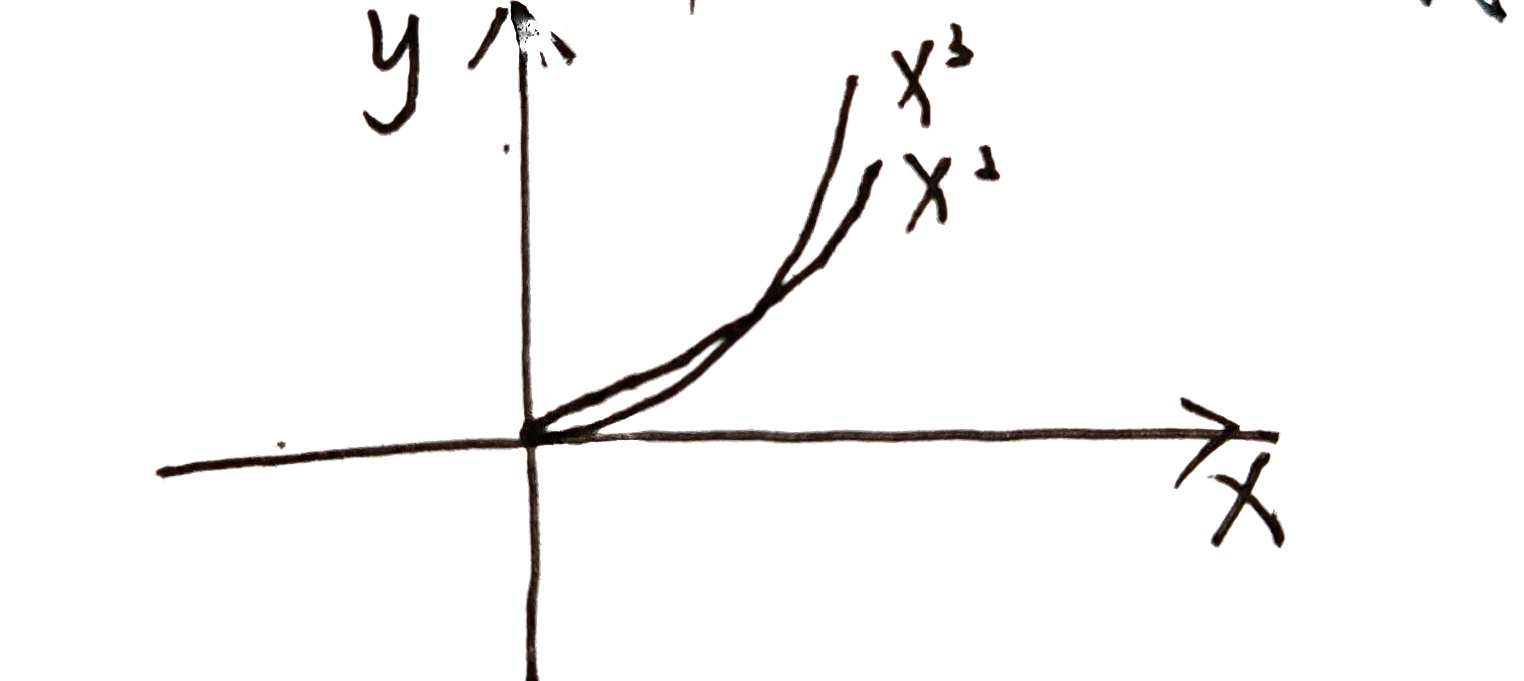
阶越高,增长速度越快
低阶能更好描述当前点,阶越高在右侧影响越大
阶乘作用
在低阶,保证 $x^5,x^6$ 次项作用(高次项) $x+\frac{x^2}{2!}+\cdots+\frac{x^5}{5!}$
在高阶,保证 $x,x^2$ 次项作用(低次项)
若无阶乘,高阶压制低阶,函数呈高次项特性
如:$x^9+x^2$
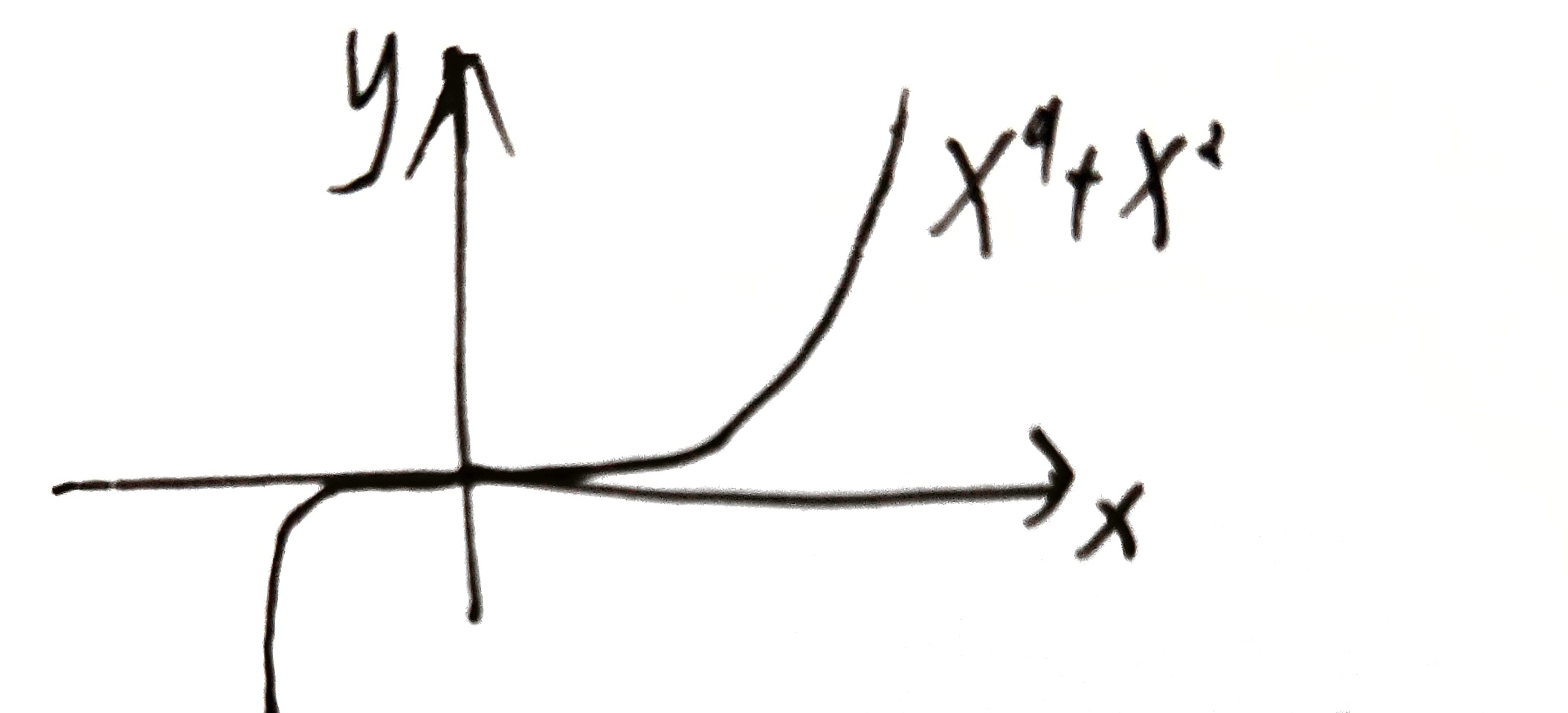
引入阶乘,图像先呈现 $x^2$ 特性,再呈现 $x^9$ 特性
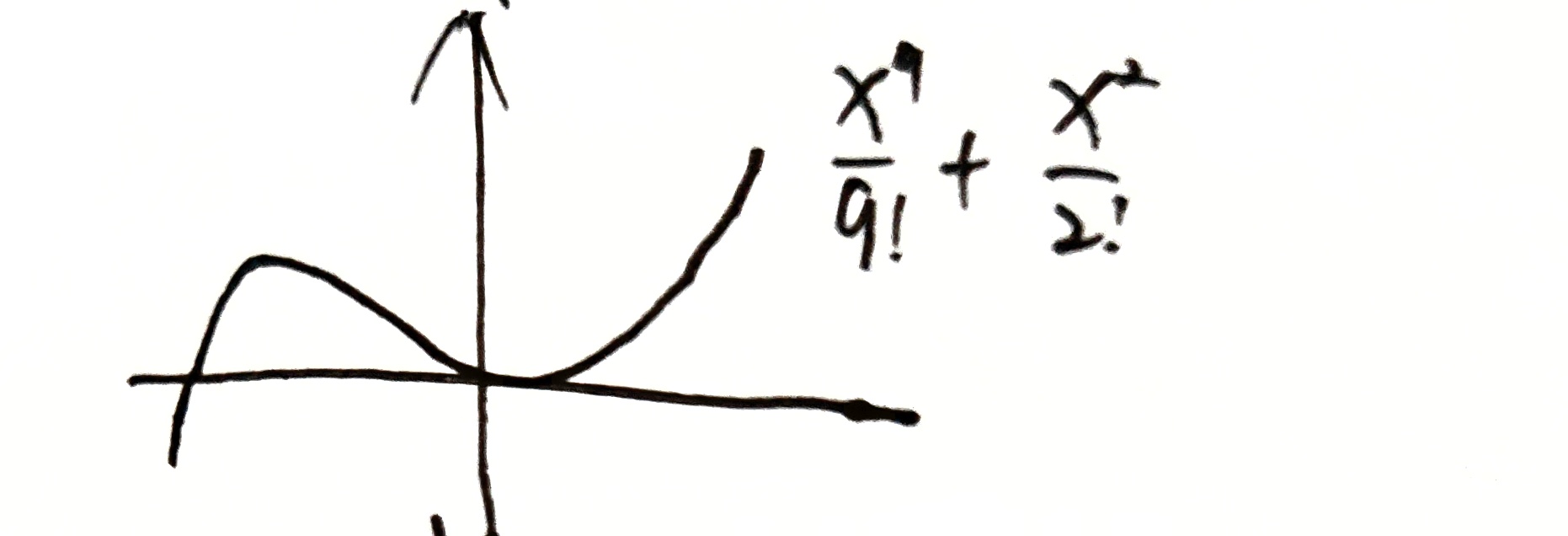
$x$ 小时,$\frac{1}{9!}$ 可限制 $x^9$ 项
随 $x$ 增加,$\frac{1}{9!}$ 作用变小,无法再限制 $x^9$
麦克劳林公式
$f(x)=f(0)+f’(0)x+f’’(0)\frac{x^2}{2!}+\cdots+f^{(n)}\frac{x^n}{n!}+f^{(n+1)}(\theta x)\frac{x^{(n+1)}}{(n+1)!},0<\theta < 1$
$sinx=f’(0)x-\frac{x^3}{3!}f^{(3)}(0)+\frac{x^5}{5!}f^{(5)}(0)-\cdots=x-\frac{x^3}{3!}+\frac{x^5}{5!}+\cdots+(-1)^{(n-1)}\frac{x^{(2n-1)}}{2n-1}$
$R_{n+1}=(-1)^{n}\frac{cos(\theta x)}{(2n+1)!}x^{(2n+1)},(0<\theta < 1)$
1.5 求极值
1.5.1 无条件极值
$z=f(x,y)$ 在 $P_0$ 邻域内连续,且有一阶、二阶偏导数,求 $z$ 在邻域内的极值
求解:
令$f_x(x,y)=0,f_y(x,y)=0\Rightarrow P_0(x_0,y_0)$
令 $A=f_{xx}(x,y)\vert _{P_0}$ ,$B=f_{xy}(x,y)\vert_{P_0}$ ,$C=f_{yy}(x,y)\vert_{P_0}$
若
- $AC-B^2>0$ ,则 $f(x,y)$ 在 $P_0$ 处为极值点
- $A>0$ ,则为极小值
- $A<0$ ,则为极大值
- $AC-B^2<0$ ,则 $f(x,y)$ 在 $P_0$ 处不是极值点
- $AC-B^2=0$ ,待定
1.5.2 条件极值
$x,y$ 满足 $\varphi(x,y)=0\varphi(x,y)=0$ , 求 $z=f(x,y)$ 的极值
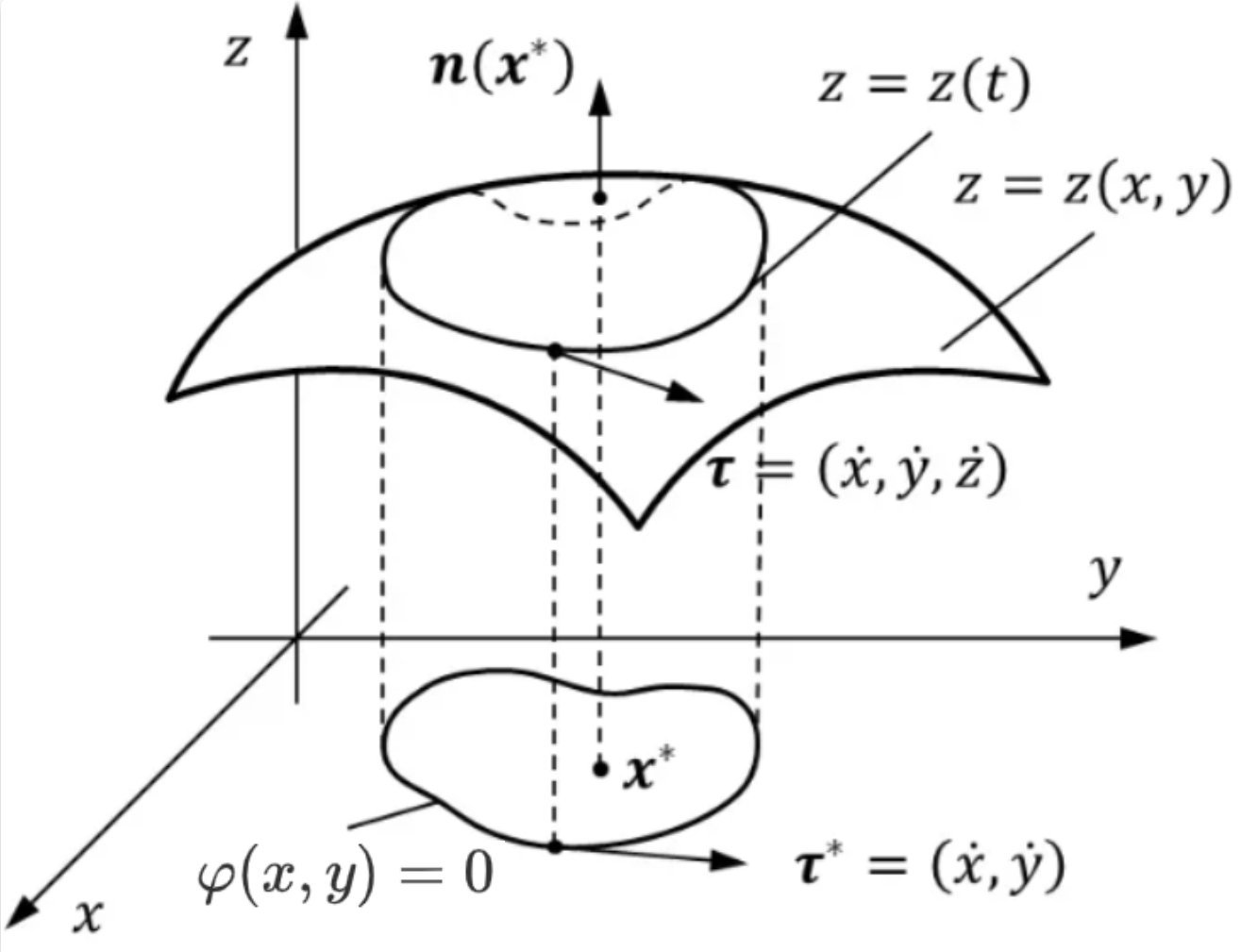
$\varphi(x,y)=0$ 为 $xoy$ 面上的曲线,将 $\varphi(x,y)=0$ 投影到曲面 $z=f(x,y)$ 上,有曲线 $\Gamma(x,y,z)$ 。
在曲线 $\Gamma$ 上找极值点为一个无条件极值问题,故用一个独立参数 $t$ 表示曲线 $\Gamma$ 不受任何约束,即 $\left\{\begin{aligned}x=x(t)\\y=y(t)\end{aligned}\right.$ ,有 $z=\{x(t),y(t)\}\Rightarrow z=z(t)$
极值条件:
显然,有 $\left(\frac{\partial \varphi}{\partial y},-\frac{\partial \varphi}{\partial x}\right)$ 与 $\bigtriangledown \phi=\left(\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}\right)$ 垂直
故可得结论:极值点处满足 $\bigtriangledown z$ 与 $\bigtriangledown \varphi$ 共线,即 $\bigtriangledown z+\lambda \bigtriangledown \varphi=0\Rightarrow \bigtriangledown\left[z(x,y)+\lambda\varphi(x,y)\right]=0$
1.5.3 多条件极值
$u=f(x,y,z,t)$ 在条件 $\varphi(x,y,z,t)=0,\psi(x,y,z,t)=0$ 下的极值,构造函数 $F(x,y,z,t)=f(x,y,z,t)+\lambda_1\varphi(x,y,z,t)+\lambda_2\psi(x,y,z,t)$
eg1
$u=x^3y^2z,x+y+z=12$ ,求最大值
构造拉格朗日函数 $F(x,y,z,t)=x^3y^2z+\lambda(x+y+z-12)=0$
令 $\left\{\begin{aligned}&F_x’=3x^2y^2z+\lambda=0\\&F_y’=2x^3yz+\lambda=0\\&F_z’=x^3y^2+\lambda=0\\&x+y+z=12\end{aligned}\right.\Rightarrow \left\{\begin{aligned}x_0=6\\y_0=4\\z_0=2\end{aligned}\right.$
1.5.4 凹函数与凸函数
已知两点 $(x,f(x))$ ,$(y,f(y))$ ,验证 $f(tx+(1-t)y)\le tf(x)+(1-t)f(y),t\in (0,1]$ ,则 $f(z)$ 为凸函数
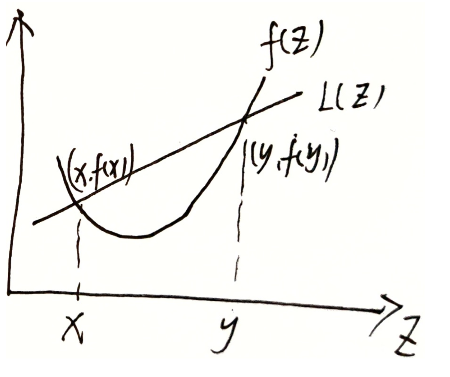
设直线 $L(z)$ 为 $Y-f(x)=\frac{f(y)-f(x)}{y-x}(X-x)$
在 $[x,y]$ 中间的任一点横坐标可表示为 $tx+(1-t)y$ ,代入后直线方程可得 $Y=\frac{f(y)-f(x)}{y-x}[tx+(1-t)y-x]+f(x)=\frac{f(y)-f(x)}{y-x}(1-t)(y-x)+f(x)=tf(x)+(1-t)f(y)$
若某一自变量曲线上值 $f(z)$ 小于直线上值 $L(z)$ , 即满足 $f(tx+(1-t)y)\le tf(x)+(1-t)f(y),t\in (0,1]$ ,函数 $f(z)$ 为凸函数
易于沿梯度寻找最优值,作为激活函数