AmosTian

0%

8.常用矩阵总结

发表于 更新于 分类于 >
本文字数 11.6k字 | 阅读时长 ≈ 40 分钟

常用矩阵总结

8.1 秩1矩阵

8.1.1 秩1矩阵特征方程

eg

image-20220914074542612

8.1.2 秩1矩阵的特征值

若 $A = A_{n\times n}$ ，$r(A)=1$ ，则全体特征值为 $\lambda(A)=\{tr(A),0,…,0\}$ ，其中 $tr(A)=a_1b_1+a_2b_2+…+a_nb_n=\beta^T\alpha$

证明：

由换位公式可知，$\alpha_{n\times 1}\beta_{1\times n}^T$ 与 $\beta_{1\times n}^T\alpha_{n\times 1}$ 相差 n-1 个零根，即有一个相等的非零特征根，而 $\beta_{1\times n}^T\alpha_{n\times 1}$ 为1阶矩阵，所以 $\lambda_1=\beta_{1\times n}^T\alpha_{n\times 1}=a_1b_1+a_2b_2+…+a_nb_n=tr(A)$

8.1.3 秩1矩阵特征向量

$A=\alpha \beta^T$ 的列向量都是 $\lambda_1=tr(A)$ 的特征向量

证明：

eg

image-20221216162018820

image-20221216163159365

8.2 优阵(正交阵)

预：非单位列向量

半：$p$ 个 $n$ 维列向量 $(p<n)$

8.2.1 预-半优阵(预-半正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_p$ 是 $n$ 维列向量，且 $p\le n$ ，且 $\alpha_1\bot\alpha_2\bot \cdots\bot\alpha_p$
，则称 $A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 为预半优阵

判定

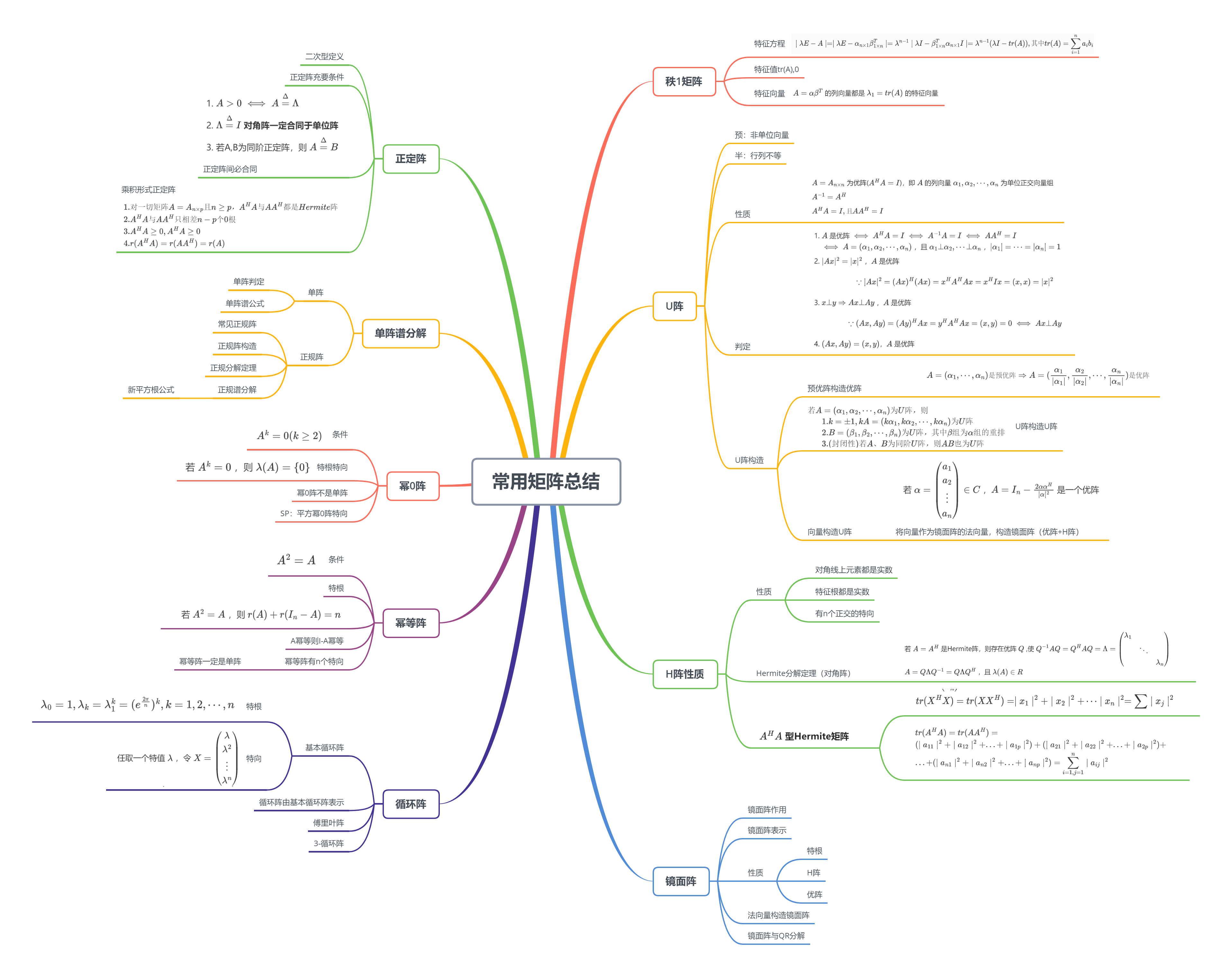
$A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 是预半优阵 $\iff A^HA=\left(\begin{matrix}(\alpha_1,\alpha_1)&\cdots&0\\\vdots&\ddots&0\\0&\cdots&(\alpha_p,\alpha_p)\end{matrix}\right)$ 是对角阵，其中 $\alpha_1,\alpha_2,\cdots,\alpha_p$ 是 $n$ 维列向量

image-20220918204358611

区分： $A^HA$ 是 $p \times p$ 阶满秩方阵，而 $AA^H$ 是 $n\times n$ 不满秩方阵

8.2.2 半优阵(半正交阵)

$A=(\alpha_1,\alpha_2,\cdots,\alpha_p)$ 是预半优阵，其中 $\alpha_i$ 是 $n$ 维列向量，若满足 $\vert \alpha_1 \vert=\vert \alpha_2 \vert=\cdots=\vert \alpha_p \vert = 1$ ，则A为半优阵

判定

$A=(\alpha_1,\cdots,\alpha_p)$ 是半优阵 $\iff \alpha_1\bot\cdots\bot\alpha_p$ ，且 $\vert \alpha_1 \vert=\cdots=\vert \alpha_p \vert=1$ $\iff A^HA=I_{p}$

性质

  1. 保模长 A为半优阵，则 $\vert Ax \vert^2=\vert x \vert^2$

    $\vert Ax \vert^2=(Ax)^H(Ax)=x^HA^HAx=\vert X\vert^2$

  2. 保正交 A为半优阵，$x\bot y$ ，则$Ax\bot Ay$

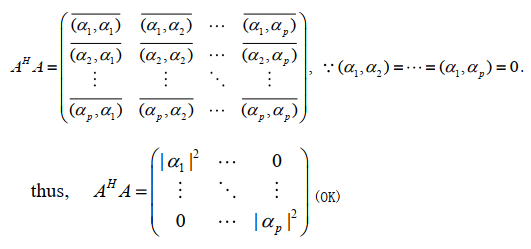
8.2.3 预优阵(预-单位正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_n$ 是 $n$ 维列向量，且 $\alpha_1\bot\alpha_2\bot\cdots\bot\alpha_n$ ，则 $A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ 是预优阵

eg

判定

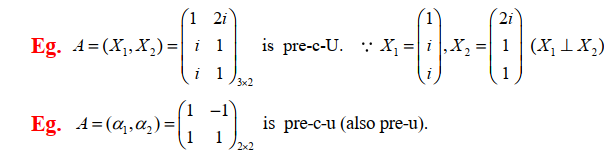
image-20220918205245673

8.2.4 优阵(正交阵)

$\alpha_1,\alpha_2,\cdots,\alpha_n$ 是 $n$ 维列向量，$\alpha_1\bot\alpha_2\bot\cdots\bot\alpha_n$ 且 $\vert \alpha_1 \vert=\cdots=\vert \alpha_n \vert=1$ ，则 $A$ 是一个优阵(正交阵)

a. 判定

  • $A=A_{n\times n}$ 为优阵($A^HA=I$)，即 $A$ 的列向量 $\alpha_1,\alpha_2,\cdots,\alpha_n$ 为单位正交向量组
  • $A^{-1}=A^H$
  • $A^HA=I,且AA^H=I$

  1. $A$ 是优阵 $\iff A^HA=I\iff A^{-1}A=I\iff AA^H=I$ $\iff A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ ，且 $\alpha_1\bot\alpha_2,\cdots\bot\alpha_n$ ，$\vert \alpha_1\vert=\cdots=\vert\alpha_n\vert=1$

  2. $\vert Ax\vert^2=\vert x \vert^2$ ，$A$ 是优阵

  3. $x\bot y \Rightarrow Ax\bot Ay$ ，$A$ 是优阵

  4. $(Ax,Ay)=(x,y)$，$A$ 是优阵

b. 优阵构造

预优阵到优阵

$A=(\alpha_1,\cdots,\alpha_n)$ 是预优阵 $\Rightarrow A=(\frac{\alpha_1}{\vert \alpha_1\vert},\frac{\alpha_2}{\vert \alpha_2\vert},\cdots,\frac{\alpha_n}{\vert \alpha_n \vert})$ 是优阵

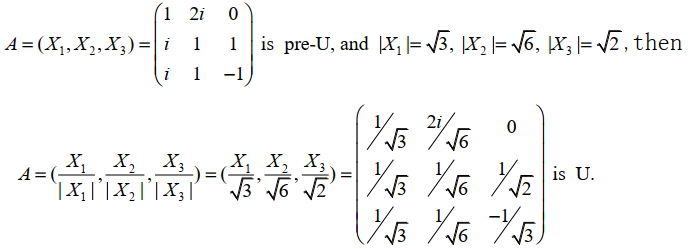
image-20220918213824439

优阵到优阵

若 $A=(\alpha_1,\alpha_2,\cdots,\alpha_n)$ 为优阵，则

  1. $k=\pm1,kA=(k\alpha_1,k\alpha_2,\cdots,k\alpha_n)$ 为优阵
  2. $B=(\beta_1,\beta_2,\cdots,\beta_n)$ 为优阵，其中 $\beta$ 组为 $\alpha$ 组的重排
  3. (封闭性)若 $A$、$B$ 为同阶优阵，则 $AB$ 也为优阵

向量构造优阵

将向量作为镜面阵的法向量，构造镜面阵（优阵+H阵）

若 $\alpha=\left(\begin{matrix}a_1\\a_2\\\vdots \\ a_n\end{matrix}\right)\in C$ ，$A=I_n-\frac{2\alpha\alpha^H}{\vert \alpha \vert^2}$ 是一个优阵

  1. $A^H=A$ 且 $A^2=I(A^{-1}=A)$

  2. $A$ 为优阵 $(A^HA=I)$

eg ：

8.3 Hermite阵

定义：$A^H=A$ ，则矩阵为 $A$

8.3.1 性质

a. 对角线上元素都是实数

证明：

$A=\left(\begin{matrix}a_{11}&\quad&\quad &\\\quad&a_{22}&\quad&\quad \\\quad &\quad&\ddots&\quad\\&\quad&\quad&a_{nn}\end{matrix}\right)$ ，而 $A^H=\left(\begin{matrix}\overline{a_{11}}&\quad&\quad &\\\quad&\overline{a_{22}}&\quad&\quad \\\quad &\quad&\ddots&\quad\\&\quad&\quad&\overline{a_{nn}}\end{matrix}\right)$ ，由Hermite性质，$A^H=A$ ，则 $a_{11}=\overline{a_{11}},a_{22}=\overline{a_{22}},…,a_{nn}=\overline{a_{nn}}$ ，可见 Hermite阵对角线元素为实数

b. 特根

若 $A^H=A$ 是Hermite矩阵，则特征根都是实数，$\{\lambda_1,\cdots,\lambda_n\}\in R$

c. 特向

若 $A=A^H\in C^{n\times n}$ ，则 $A$ 有 $n$ 个互相正交的特征向量，即 $X_1\bot X_2\bot…\bot X_n$

推论

若 $A$ 为Hermite阵 $A^H=A$ ,且 $\lambda_1 \neq \lambda_2$ ，则相应的特征向量正交

证明：

8.3.2 Hermite分解定理（对角阵）

若 $A=A^H$ 是Hermite阵，则存在优阵 $Q$ ,使 $Q^{-1}AQ=Q^HAQ=\Lambda=\left(\begin{matrix}\lambda_1&\quad&\quad\\\quad&\ddots&\quad\\\quad&\quad&\lambda_n\end{matrix}\right)$ $A=Q\Lambda Q^{-1} = Q\Lambda Q^H$ ，且 $\lambda(A)\in R$

8.3.3 $A^HA$ 型的 $Hermite$ 矩阵

任一矩阵 $A_{n\times p}$ ，$A^HA$ 与 $AA^H$ 都是 $Hermite$ 矩阵

a. 向量 $XX^H$ 的迹

  • $tr(XY^H)=tr(Y^HX)=x_1\overline{y_1}+\cdots+x_n\overline{y_n} =\sum\limits_{i=1}\limits^{n}x_i\overline{y_i}$ ，$X$ 为列向量

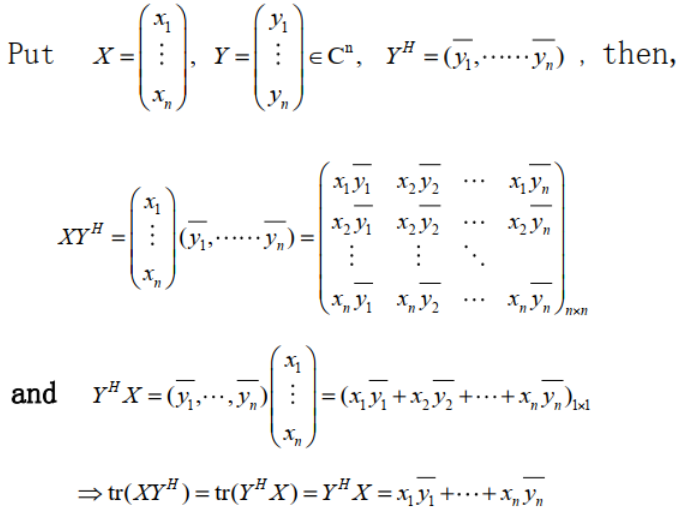
    image-20220918005502843

b. 矩阵 $A^HA$ 的迹

$A_{n\times p}=\left(\begin{matrix}a_{11}&\cdots&a_{1p}\\\vdots&\ddots&\vdots\\a_{n1}&\cdots&a_{np}\end{matrix}\right)\in C^{n\times p}$ ，$A^H_{p\times n}=\left(\begin{matrix}\overline{a_{11}}&\cdots&\overline{a_{n1}}\\\vdots&\ddots&\vdots\\\overline{a_{1p}}&\cdots&\overline{a_{np}}\end{matrix}\right)\in C^{p\times n}$

image-20220917235434977

推论

$tr(AB^H)=tr(B^HA)=\sum a_{ij}\overline{b_{ij}}$

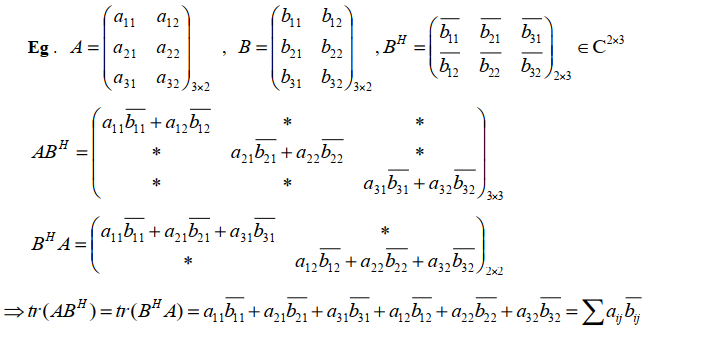
image-20220918001146003

  • 将 A、B 矩阵按列分块，可验证 $tr(B^HA)$

  • 将 A、B 矩阵按行分块，可验证 $tr(AB^H)$

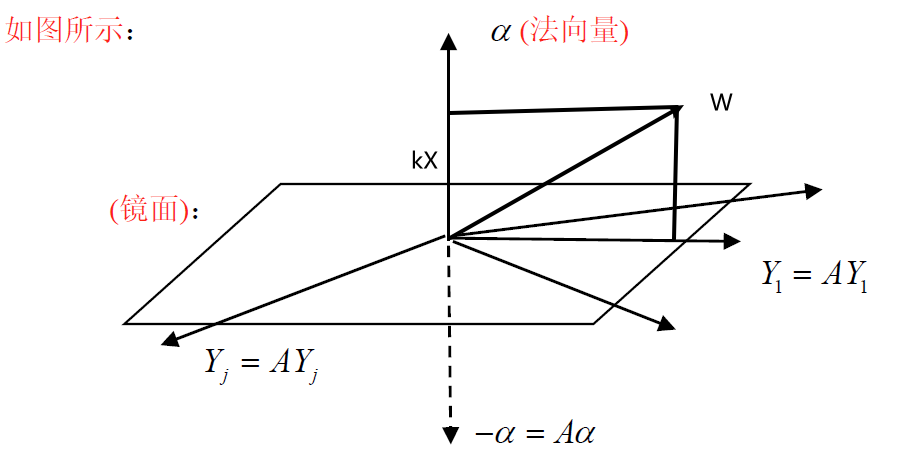
8.4 镜面阵

法向量确定一个镜面

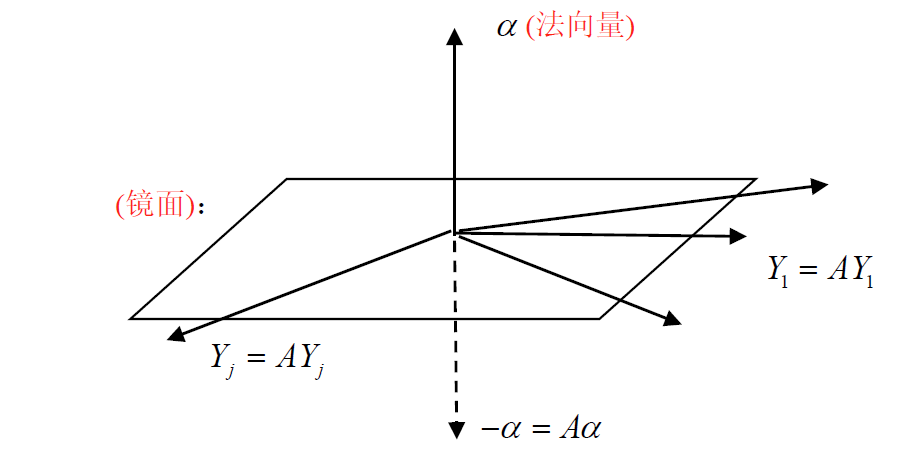
image-20230106171901212

8.4.1 镜面阵的作用

对法向量

  • $A\alpha=-\alpha$
  • $A(A\alpha)=A^2\alpha=\alpha$

对镜面上向量

  • $AY=Y$

8.4.2 镜面阵表示

令 $\epsilon=\frac{\alpha}{\vert \alpha\vert}$ ，镜面阵 $A=I-2\epsilon\epsilon^H$ ，满足 $\epsilon^H\epsilon=\vert\epsilon\vert^2=1$

验证：

8.4.3 性质

a. 特根

镜面阵至少有两个特征向量 $\alpha$ 与 $Y$

  • $A\alpha=-\alpha$ ，特根为 $-1$
  • $AY=Y$ ，特根为 $1$

代数方法求特根

特征多项式 $\vert \lambda I-A\vert=(\lambda+1)(\lambda-1)^{n-1}$

b. 特向

镜面上有 $n-1$ 个独立的(线性无关)向量，$Y_1,Y_2,\cdots,Y_{n-1}$ $(AY_1=Y_1,AY_2=Y_2,\cdots,AY_{n-1}=Y_{n-1})$ 都是 $1$ 的特向

  • $Y_1,Y_2,\cdots,Y_{n-1}$ 为 $\alpha^HX=0$ 的 $n-1$ 个线性无关的解

    证明：

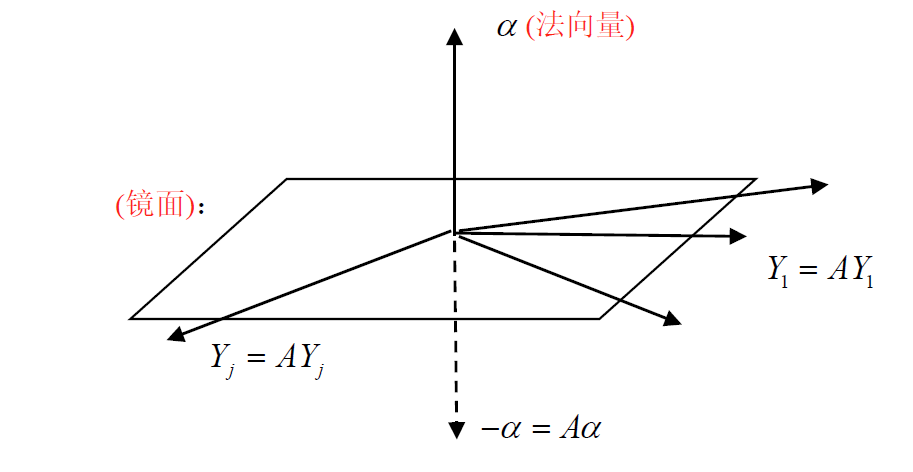
image-20230106171901212

  • 镜面阵内 $n-1$ 个特征向量有不同选法，可取 $Y_1\bot Y_2\bot\cdots\bot Y_{n-1}$ (互正交)，故可对镜面阵有 $n$ 个正交特向 $\{X\bot Y_1\bot Y_2\bot \cdots \bot Y_{n-1}\}$

    正规阵，Hermite阵有 $n$ 个相互正交的向量

$A$ 的全体特根为 $\lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1个1}\}$

c. 镜面阵为 $Hermite$ 阵

$A=I_n-\frac{2(\alpha\alpha^H)}{\vert \alpha\vert^2}$ Hermite阵的差

d. $A^2=I$

$A^2\alpha=A(A\alpha)=A(-\alpha)=-(A\alpha)=-(-\alpha)=\alpha$

即证明： $A^2=I$

image-20230106175439693

d. $A^{-1}=A$

e. $A$ 为优阵

由于 $A^H=A$ ，且 $A^{-1}=A$ ，故 $A^HA=A^{-1}A=I$ ，$A$ 为优阵

特根 $\lambda(A)=\{-1,\underbrace{1,\cdots,1}_{n-1}\}$ ，特向 $\alpha\bot Y_1\bot\cdots\bot Y_{n-1}$ ，优阵 $Q=\left(\frac{\alpha}{\vert \alpha\vert},\frac{Y_1}{\vert Y_1\vert},\cdots,\frac{Y_{n-1}}{\vert Y_{n-1}\vert}\right)$ ，$Q^{-1}=Q^H$

$\Rightarrow Q^{-1}AQ=Q^HAQ=D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right)$ 为对角阵

$D=\left(\begin{matrix}-1&&&\\&1&&\\&&\ddots&\\&&&1\end{matrix}\right)$ 为一个特殊镜面阵，法向量指向 $x$ 轴方向

8.4.3 向量构造镜面阵

设 $R^n$ 中2个 实向量，$\alpha=\left(\begin{matrix}a_1\\\vdots\\a_n\end{matrix}\right),\beta=\left(\begin{matrix}b_1\\\vdots\\b_n\end{matrix}\right)\in R^n$ ，且 $\left\{ \begin{aligned}&\vert\alpha\vert=\vert\beta\vert\\&\alpha\neq \beta\end{aligned}\right.$ ，则有镜面阵 $P=I-\frac{2(\alpha-\beta)(\alpha-\beta)^H}{\vert (\alpha-\beta)\vert^2}$ ，使得 $P\alpha=\beta,P\beta=\alpha$

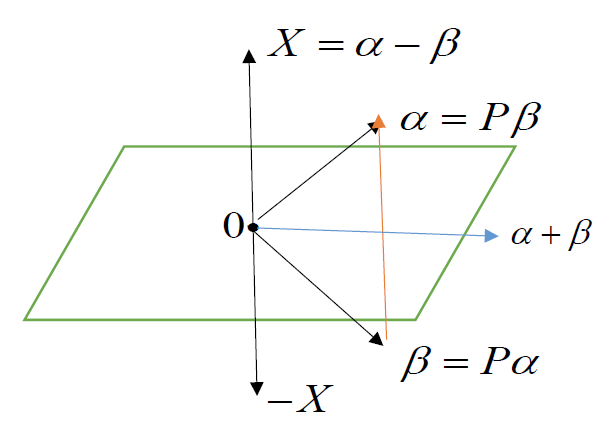
image-20230106212814216.

证明：

eg

image-20230106223537609

8.4.4 镜面阵与QR分解

$P_{i}$ 表示 $i$ 阶镜面阵 ，$A_{i}$ 表示 $i$ 阶方阵

故有镜面阵 $Q=P_n\left(\begin{matrix}1&0\\0&P_{n-1}\end{matrix}\right)\cdots\left(\begin{matrix}1&0&0&\cdots&0\\0&1&0&\cdots&0\\0&0&1&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&P_{2}\end{matrix}\right)$ ，使 $QA=R$ ，由于镜面阵为优H阵 $Q^H=Q^{-1}=Q$ ，故有 $QR$ 分解 $A=QR$

2阶例题

image-20230107163412850

3阶例题

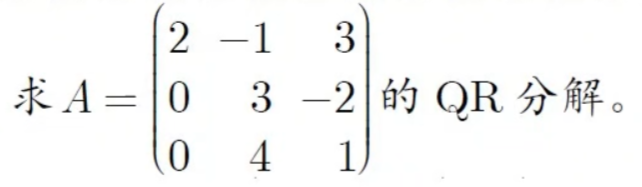
image-20230107171310008

8.5 正定阵

8.5.1 二次型

a. 二次型定义

令 $A$ 为 $Hermite$ 阵 $(A^H=A\in C^{n\times n})$， $X=\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)$ ，称 $X^HAX=\left(\overline{x_1},\overline{x_2},\cdots,\overline{x_n}\right)A\left(\begin{matrix}x_1\\x_2\\\vdots\\x_n\end{matrix}\right)$ ，为矩阵 $A$ 产生的二次型，记为 $f(x)=X^HAX$

b. 正定二次型与正定阵定义

若 $A^H=A$ ,对一切 $X\neq 0$ ,有 $X^HAX>0$ ,则 $f(x)=X^HAX$ 为正定二次型，A为正定阵，记为 $A>0$
若 $A^H=A$ ,对一切 $X\neq 0$ ，有 $X^HAX\ge 0$ ,则 $f(x)=X^HAX$ 为半正定二次型，A为半正定阵，记为 $A\ge 0$

8.5.2 正定阵的定理

$A>0\iff$ $A$ 为Hermite阵，且 $\lambda_1,\lambda_2,\cdots,\lambda_n > 0$
$A\ge 0 \iff$ $A$ 为Hermite阵，且 $\lambda_1,\lambda_2,\cdots,\lambda_n \ge 0$

证明

$\Rightarrow$

若 $A$ 为正定阵，则 $A$ 生成的二次型 $f(x)=X^HAX>0$ ，$\therefore \lambda_i=\frac{X^HAX}{\vert X\vert^2}>0$

$\Leftarrow$

单位阵是正定阵 ：$\lambda_i= 1$ 显然大于0

8.5.3 正定阵间必合同

  1. $A>0（正定阵） \iff A\overset{\Delta}{=}\Lambda$
  2. $\Lambda\overset{\Delta}{=}I$ 对角阵一定合同于单位阵
  3. 若A,B为同阶正定阵，则 $A\overset{\Delta}{=} B$

证明1：

证明2：

证明3：

8.5.4 乘积形式的正定阵

  1. 对一切矩阵 $A=A_{n\times p}$ 且 $n\ge p$ ，$A^HA$ 与 $AA^H$ 都是Hermite阵
  2. $A^HA$ 与 $AA^H$ 只相差 $n-p$ 个0根
  3. $A^HA\ge0$ ，$A^HA\ge 0$
  4. $r(A^HA)=r(AA^H)=r(A)$

a. $A^HA$ 为Hermite阵

b. $A^HA与AA^H$ 相差n-p个0根

c. $A^HA与AA^H$ 是半正定阵（不是方阵的正定阵）

d. $r(AA^H)=r(A^HA)=r(A)$

8.6 单阵

单阵 $A$（又叫单纯阵，可对角阵），即满足 $P^{-1}AP=D=\left(\begin{matrix}\lambda_1&&0\\&\ddots&\\0&&\lambda_n\end{matrix}\right)$ ， $P$ 可逆， $P$ 中列向量为 $A$ 的特征向量

8.6.1 单阵谱公式

若 $A$ 为单阵，全体不同特征根为 $\lambda_1,\lambda_2,\cdots,\lambda_k$ ，则有 $A=\lambda_1G_1+\cdots+\lambda_kG_k$ 为 $A$ 的谱分解

满足性质：

  • 谱阵： $G_i=\frac{(A-\lambda_1)\cdots(A-\lambda_{i-1})(A-\lambda_{i+1})\cdots(A-\lambda_k)}{(\lambda_i-\lambda_1)\cdots(\lambda_i-\lambda_{i-1})(\lambda_i-\lambda_{i+1})\cdots(\lambda_i-\lambda_k)}$，谱阵 $G_1,\cdots,G_k$ 中各列都是A的特征向量
  • 和为单位阵： $G_1+G_2+\cdots+G_k=I$
  • 相互正交： $G_1G_2=0,\cdots,G_iG_j=0(i\neq j)$
  • 幂等： $G_1^2=G_1,\cdots,G_k^2=G_k$ ，但 $G_1^H=G_1,\cdots,G_k^H=G_k$ 不一定成立

a. 单阵谱函数

$f(A)=f(\lambda_1)G_1+\cdots+f(\lambda_k)G_k$

幂次

$A^p=\lambda_1^pG_1+\cdots+\lambda_k^pG_p,p=0,1,…$

单阵逆公式

$A^{-1}=\frac{1}{\lambda_1}G_1+\frac{1}{\lambda_2}G_2+\cdots+\frac{1}{\lambda_k}G_k$ ，其中 $A$ 为单阵

b. 单阵函数公式

若 $f_1(x),f_2(x),\cdots,f_k(x)$ 为 $x$ 的 $k-1$ 次多项式，且 $f_1(x)+f_2(x)+\cdots+f_k(x)=1$ ，则 $f_1(A)+f_2(A)+\cdots+f_k(A)=I$ ，$f_1(A),\cdots,f_k(A)$ 中非0列都是 $A$ 的特征向量

8.6.2 单阵判定

a. 充分条件

若存在可逆阵 $P$ ，使 $A$ 相似于对角阵，则 $A$ 为单阵

  1. 单阵特例

    image-20221107205702307

    $A$ 为正规阵，则 $A$ 必相似于对角阵

    证： $A$ 为正规阵，则存在U阵 $Q$ 使 $Q^HAQ= \Lambda$ ，使A阵U相似于对角阵，故正规阵一定是单阵

  2. 设 $n$ 阶方阵 $A$ 恰有 $n$ 个不同根 $\lambda_1,\cdots,\lambda_n$ ，则 $A$ 为单阵（必相似于对角阵）

  3. A有 $n$ 个无关的特征向量 $X_1,X_2,\cdots,X_n$

    令 $P=\left(X_1,X_2,\cdots,X_n\right) \Rightarrow P^{-1}AP=D$

  4. 若每个 $k$ 重根 $\lambda$ ，恰有 $k$ 个特征向量，则 $A$ 为单阵

    • 方程 $(A-\lambda_1)X=0$ 有 $n-r(A-\lambda_1I)$ 个基本解 $\Rightarrow AX=\lambda_1X 有n-r(A-\lambda_1I)个基本解$

      常通过判断 $r(A-重根I)$ 判断A是否为单阵

      $\Rightarrow r(A-\lambda_1I)=n-k$ ，$\lambda_1$ 有k个特征向量 ，则A可能是单阵

      $\Rightarrow r(A-\lambda_1I)\neq n-k$ ，则A必不是单阵

    • eg1

      验证A是否为单阵：

    • eg2

      验证A是否为单阵：

  5. 设 $\lambda_1,\lambda_2,\cdots,\lambda_k$ 为A的全体不同根

    Cayley定理：

    若方阵 $A$ 的特征多项式 $T(x)=\vert A-x I\vert=c_0+c_1x+c_2x^2+\cdots+c_nx^n$ ，则 $T(A)=c_0I+c_1A+c_2A^2+\cdots+c_nA^n=0$

    • 方阵A的特征多项式可分解为 $T(x)=(x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_n)$ 满足 $T(A)=(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_nI)=0$

    若 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)=0$ ，则 $A$ 为单阵( $A$ 相似于对角阵)
    若 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)\neq 0$ ，则 $A$ 不是单阵

    eg

    上述判定方法也适用于分块阵

b. 单阵充要条件：0化式判别法(了解，判断用重根矩阵秩)

0化式与极小式定义

若多项式 $f(x)$ 使 $f(A)=0$ ，则称 $f(x)$ 为 $A$ 的0化式

极小式为次数最少的0化式 ： 若 $\lambda_1,\cdots,\lambda_k$ 为不同根，且 $(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_kI)=0$ ，则 $A$ 必为单阵，此时称 $m(x)=(x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_k)$ 为 $A$ 的极小式

  • eg1：

  • eg2:

    极小式求法

  1. 对于 $\vert xI-A \vert=(x-a)^2(x-b)=0$

    • 若 $(A-aI)(A-bI)=0$ ，则极小式为 $m(x)=(x-a)(x-b)$

    • 若 $(A-aI)(A-bI)\neq 0$ ，则极小式为 $m(x)=(x-a)^2(x-b)$

  2. 对于 $\vert xI-A \vert=(x-a)(x-b)(x-c)$ ，则极小式为 $m(x)=(x-a)(x-b)(x-c)$

若f(x)=0无重根，且f(A)=0,则A必为单阵

定理：

  • 若 $f(A)=0$ ，则 $f(A)g(A)=0$ ,可知 $f(x)g(x)$ 也是0化式

  • 特征多项式 $f(x) = \vert xI-A \vert=a_0+a_1x+a_2x^2+\cdots+a_nx^n$ 一定是0化式，即 $f(A)=a_0+a_1A+\cdots+a_nA^n=0$

  • 极小式为特征多项式的因式，可表示为 $\vert xI-A \vert=m(x)g(x)$

  • 极小式必为每个0化式 $f_i(x)$ 的因子，即若 $f_i(A)=0$ ，则 $f_i(x)=m(x)g_i(x)$

应用

  1. 列出特征方程，求出极小式，即证明A是单阵
  2. 根据极小式，写出单阵谱分解
  3. 计算f(A)

8.6.3 正规阵

a. 定义

若方阵A满足 $A^HA=AA^H$ ，则A为正规阵

正规条件：$A^HA=AA^H$

b. 正规阵特点

  1. 正规阵必为方阵 ($A^HA与AA^H$ 的阶数相等，即行列数相等)
  2. $A正规\iff A^H正规$ ，$A不正规\iff A^H不正规$

c. 常见正规阵

对角阵

对角阵 $A=\left(\begin{matrix}a_1&&\\&\ddots&\\&&a_n\end{matrix}\right)$ 必正规

三角正规阵必对角

若三角阵 $B=\left(\begin{matrix}b_{1}&b_{12}&\cdots&b_{1n}\\&b_{2}&\cdots&b_{2n}\\&&\ddots&\\&&&b_n\end{matrix}\right)$ 正规，则 $B=\left(\begin{matrix}b_1&&&\\&b_2&&\\&&\ddots&\\&&&b_n\end{matrix}\right)$ 为对角形

证明：严格三角阵不是正规阵

若分块阵 $A=\left(\begin{matrix} B&C\\0&D \end{matrix}\right)$ 正规，则 $C=0$ ，且 $B，D$ 都正规，即 $A=\left(\begin{matrix} B&0\\0&D \end{matrix}\right)$

由证明过程可见，严格三角阵为非正规阵

H阵与斜H阵

Hermite阵与斜Hermite阵必正规

  • 实对称阵与反对称阵都是正规阵
优阵

优阵必正规（实正交阵）

e. 正规阵的构造方法

倍数法则

若 $A$ 正规，取倍数 $k$ ，则 $kA$ 为正规阵

平移法则

若 $A$ 正规，则 $A\pm cI$ 正规

优相似

若 $A$ 正规，则 $Q^HAQ$ 也正规，其中 $Q$ 为优阵($Q^H=Q^{-1}$)，即正规阵的优相似阵一定正规

证明：

多项式正规

若 A 正规，则 $f(A)=\lambda_0I+\lambda_1A+\lambda_2A^2+\cdots+\lambda_nA^K$ 正规

f. 正规阵与其H阵的特征向量相同

若A正规，则 $A^H$ 与 A 有相同的向量

证明

8.7 幂0阵

8.7.1 条件

$A^k=0(k\ge 2)$ ，且 $A\neq 0$ ，则为 $k$ 次幂0阵

  • 若 $(A-bI)^k=0$ ，$A\neq bI$ ，则 $A$ 为平移幂0阵

8.7.2 特根特向

若 $A^k=0$ ，则 $\lambda(A)=\{0\}$

  • 由 Cayley 定理，$\lambda^k=0\Rightarrow \lambda=0$
  • 由特向(4.1)求法，$A\cdot A=0$ ，则 $A$ 中各列都是0根的特向

若 $(A-bI)^k=0\Rightarrow \lambda(A)=\{b,\cdots,b\}$

8.7.3 幂0阵不是单阵

推论：$A$ 与 $A-bI$ 同为单阵或非单阵，则 平移不改变单阵或非单阵

  • 若 $(A-bI)^k=0$ 且 $A-bI\neq 0$ 则A非单阵 ，且 $\lambda(A)=\{b,b,\cdots,b\}$

    则 $f(A)=f(b)I+\frac{f’(b)}{1!}(A-bI)+\frac{f’’(b)}{2!}(A-bI)^2+\cdots \frac{f^{k-1}(b)}{(k-1)!}(A-bI)^{k-1}$ 为 $f(x)$ 的解析式

8.7.4 记忆：平方幂0

若 $A^2=0(A\neq 0)$ ，则A中列都是0根特向

  • A中列 $\left(\begin{matrix}1\-1\end{matrix}\right),\left(\begin{matrix}1\\1\end{matrix}\right)$ 为 $\lambda=0$ 的特向

eg

8.8 幂等阵性质

幂等条件：$A^2=A$

特根：$\lambda(A)=1或0$

8.8.1 幂等阵一定为单阵(相似于对角阵)

$A\sim D=\left(\begin{matrix}1\\&\ddots\\&&1\\&&&0\\&&&&\ddots\\&&&&&0\end{matrix}\right)$

单阵引理：

  • $f(x)$ 为A的0化式，若 $f(A)=0$ ,且f(x)无重根，则A为单阵

8.8.2 r(A)与r(I-A)关系

若 $A^2=A$ ，则 $r(A)+r(I_n-A)=n$

8.8.3 A幂等$\iff$ I-A幂等

$A^2=A\iff (I-A)^2=(I-A)$

  • 则有 $tr(I-A)=tr(I)-tr(A)=n-r=r(I-A)$

证明：

8.8.4 幂等阵的特向

A是幂等阵，则 $A$ 有 $n$ 个无关特向

8.8.5 谱分解中谱阵为幂等阵

谱分解 $A=\lambda_1G_2+\cdots+\lambda_kG_k$ 中 $G_i$ 为幂等阵（$G_1^2=G_1,\cdots,G_k^2=G_k$

8.9 循环矩阵

$n$ 阶循环阵定义为：$C=[c_0,c_1,\cdots,c_{n-1}]\left(\begin{matrix}c_0&c_1&c_2&\cdots&c_{n-1}\\c_{n-1}&c_0&c_1&\cdots&c_{n-2}\\\vdots&\vdots&\vdots&\ddots&\vdots\\c_1&c_{2}&c_{3}&\cdots&c_{0}\end{matrix}\right)$

8.9.1基本循环阵

$A=[1,0\cdots,0]=\left(\begin{matrix}0&1&0&\cdots&0\\0&0&1&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&1\\1&0&0&\cdots&0\end{matrix}\right)\xlongequal{按列}(e_n,e_1,e_2,\cdots,e_{n-1})\xlongequal{按行}\left(\begin{matrix}e_2^{H}\\e_3^{H}\\\vdots\\e_{n}^H\\e_{1}^H\end{matrix}\right)$

a. $A$ 特根

由 $A^n=I\Rightarrow\lambda(A^n)=\{\lambda_1^n,\lambda_2^n,\cdots,\lambda_n^n\}=\lambda(I)=\{1,1,\cdots,1\}$ ，有 $\lambda_1^n=1,\lambda_2^n=1,\cdots,\lambda_n^n=1$

$\lambda^n=1$ 的根恰是单位圆上的 $n$ 个分点，$\lambda_0=1$ ，$\lambda_1=e^{\frac{2\pi}{n}i}=\cos\frac{2\pi}{n}+isin\frac{2\pi}{n}$ ，$\lambda_2=e^{\frac{2\pi}{n}2i}$ ，$\cdots$ ，$\lambda_{n-1}=e^{\frac{2\pi}{n}(n-1)i}$

  • $\lambda_0=1,\lambda_k=\lambda_1^k=(e^{\frac{2\pi}{n}})^k,k=1,2,\cdots,n$

  • $\lambda_k^n=1$

b. $A$ 的特向

任取一个特值 $\lambda$ ，令 $X=\left(\begin{matrix}\lambda\\\lambda^2\\\vdots\\\lambda^n\end{matrix}\right)$ ，$\Rightarrow AX=\left(\begin{matrix}0&1&0&\cdots&0\\0&0&1&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&1\\1&0&0&\cdots&0\end{matrix}\right)\left(\begin{matrix}\lambda\\\lambda^2\\\vdots\\\lambda^{n-1}\\\lambda^n\end{matrix}\right)=\left(\begin{matrix}\lambda^2\\\lambda^3\\\vdots\\\lambda^{n-1}\\\lambda\end{matrix}\right)=\left(\begin{matrix}\lambda^2\\\lambda^3\\\vdots\\\lambda^{n-1}\\\lambda^{n+1}\end{matrix}\right)=\lambda\left(\begin{matrix}\lambda\\\lambda^2\\\vdots\\\lambda^{n-1}\\\lambda^n\end{matrix}\right)=\lambda X$

故取 $\lambda_0=1$ ，$\lambda_1=e^{\frac{2\pi}{n}i}$ ，$\lambda_2=e^{\frac{2\pi}{n}2i}$ ，$\cdots$ ，$\lambda_{n-1}=e^{\frac{2\pi}{n}(n-1)i}$

令 $X_0=\left(\begin{matrix}\lambda_0\\\lambda_0^2\\\vdots\\\lambda_0^n\end{matrix}\right)=\left(\begin{matrix}1\\1\\\vdots\\1\end{matrix}\right)$ ，$X_1=\left(\begin{matrix}\lambda_1\\\lambda_1^2\\\vdots\\\lambda_1^n\end{matrix}\right)$ ，$\cdots$ ，$X_{n-1}=\left(\begin{matrix}\lambda_{n-1}\\\lambda_{n-1}^2\\\vdots\\\lambda_{n-1}^n\end{matrix}\right)$

  • 或可写作： $X_0=\left(\begin{matrix}1\\1\\\vdots\\1\end{matrix}\right)$ ，$X_1=\left(\begin{matrix}1\\\lambda_1\\\vdots\\\lambda_1^{n-1}\end{matrix}\right)=\left(\begin{matrix}\lambda_1^n\\\lambda_1\\\vdots\\\lambda_1^{n-1}\end{matrix}\right)$ ，$\cdots$ ，$X_{n-1}=\left(\begin{matrix}1\\\lambda_{n-1}\\\vdots\\\lambda_{n-1}^{n-1}\end{matrix}\right)=\left(\begin{matrix}\lambda_{n-1}^n\\\lambda_{n-1}\\\vdots\\\lambda_{n-1}^{n-1}\end{matrix}\right)$

$\vert X_0\vert^2=\vert X_1\vert^2=\cdots=\vert X_{n-1}\vert^2=n$ ，且 $X_0\bot X_1\bot\cdots\bot X_{n-1}$ ，$\vert X_j\vert=\sqrt{n}$

8.9.2 循环阵可由基本循环阵表示

  • $A^0=(e_1,e_2,e_3,\cdots,e_{n})=I$
  • $A^1=(e_n,e_1,e_2,\cdots,e_{n-1})$
  • $A^2=(e_{n-1},e_{n},e_1,\cdots,e_{n-2})$
  • $A^{n-1}=(e_2,e_3,e_4,\cdots,e_1)$
  • $A^n=(e_1,e_2,e_3,\cdots,e_n)$

令矩阵函数 $f(A)=c_0I+c_1A+c_2A_2+\cdots+c_{n-1}A^{n-1}=C$

  • 可知基本循环阵 $A$ 正规 $\Rightarrow f(A)$ 正规，$C$ 正规
  • $A$ 与 $f(A)$ 有相同特向，$\lambda(A)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\}$ ，$\lambda(f(A))=\{f(\lambda_1),f(\lambda_2),\cdots,f(\lambda_n)\}$

8.9.3 傅里叶阵

令 $Q=\left(\frac{X_0}{\vert X_0\vert},\frac{X_1}{\vert X_1\vert},\cdots,\frac{X_{n-1}}{\vert X_{n-1}\vert}\right)=\frac{1}{\sqrt{n}}\left(X_0,X_1,\cdots,X_{n-1}\right)$ 为优阵（傅里叶阵）

$\Rightarrow Q^{-1}AQ=Q^HAQ=D=\left(\begin{matrix}\lambda_0&&&\\&\lambda_1&&\\&&\ddots&\\&&&\lambda_{n-1}\end{matrix}\right)$

因为 $C=f(A)$ 与 $A$ 有相同的特向 ，有相同的优阵 $Q$

$\Rightarrow Q^{-1}CQ=Q^{-1}f(A)Q=Q^Hf(A)Q=D=\left(\begin{matrix}f(\lambda_0)&&&\\&f(\lambda_1)&&\\&&\ddots&\\&&&f(\lambda_{n-1})\end{matrix}\right)$

8.9.4 3-循环阵

求 3-循环阵 $A=[a_0,a_1,a_2]=\left(\begin{matrix}a_0&a_1&a_2\\a_2&a_0&a_1\\a_1&a_2&a_0\end{matrix}\right)$ 的三个正交特征向量

令基本循环阵 $\Omega=(e_3,e_1,e_2)=\left(\begin{matrix}0&1&0\\0&0&1\\1&0&0\end{matrix}\right)$ ，有基本循环阵性质可知 $\Omega^3=I$ ，特根

$\lambda(\Omega)=\{\lambda_1,\lambda_2,\lambda_3\}$ 为平面上单位圆周的三等分点，满足 $\lambda_1^3=\lambda_2^3=\lambda_3^3=1$

$\lambda_j=e^{\frac{2\pi}{3}ji},j=1,2,3$

令 $X_j=\left(\begin{matrix}\lambda_1\\\lambda_1^2\\\lambda_1^3\end{matrix}\right)$ ，可知 $\Omega X_j=\Omega \left(\begin{matrix}\lambda_j\\\lambda_j^2\\\lambda_j^3\end{matrix}\right)=\left(\begin{matrix}\lambda_j^2\\\lambda_j^3\\\lambda_j\end{matrix}\right)=\left(\begin{matrix}\lambda_j^2\\\lambda_j^3\\\lambda_j^4\end{matrix}\right)=\lambda_j\left(\begin{matrix}\lambda_j\\\lambda_j^2\\\lambda_j^3\end{matrix}\right)=\lambda_jX_j$

即 $X_j$ 是属于 $\lambda_j$ 的 $\Omega$ 的特向，故 $\Omega$ 恰有3个特向 $X_1,X_2,X_3$ 且 $X_1\bot X_2 \bot X_3$ ，$\vert X_1\vert=\vert X_2\vert=\vert X_3\vert=\sqrt{3}$

令优阵 $Q=(q_1,q_2,q_3)=\left(\frac{X_1}{\vert X_1\vert},\frac{X_2}{\vert X_2\vert},\frac{X_3}{\vert X_3\vert}\right)=\frac{1}{\sqrt{3}}\left(\begin{matrix}\lambda_1&\lambda_2&\lambda_3\\\lambda_1^2&\lambda_2^2&\lambda_3^2\\\lambda_1^3&\lambda_2^3&\lambda_3^3\end{matrix}\right)$ (为傅里叶优阵)

可得优分解 $Q^{-1}\Omega Q=D\left(\begin{matrix}\lambda_1&&\\&\lambda_2&\\&&\lambda_3\end{matrix}\right)$ ，其中 $\Omega=(e_3,e_1,e_2)=\left(\begin{matrix}0&1&0\\0&0&1\\1&0&0\end{matrix}\right)$

  • 或者 $Q=\frac{1}{\sqrt{3}}\left(\begin{matrix}1&1&1\\\lambda_1&\lambda_2&\lambda_3\\\lambda_1^2&\lambda_2^2&\lambda_2^2\end{matrix}\right)$ ， $\Omega=\left(\begin{matrix}0&1&0\\0&0&1\\1&0&0\end{matrix}\right)$ 特向 $\left(\begin{matrix}1\\\lambda_1\\\lambda_1^2\end{matrix}\right),\left(\begin{matrix}1\\\lambda_2\\\lambda_2^2\end{matrix}\right),\left(\begin{matrix}1\\\lambda_3\\\lambda_3^2\end{matrix}\right)$

    优分解 $Q^{-1}\Omega Q=D=\left(\begin{matrix}\lambda_1&&\\&\lambda_2&\\&&\lambda_3\end{matrix}\right)$

可写 3-循环阵 $A=[a_0,a_1,a_2]=\left(\begin{matrix}a_0&a_1&a_2\\a_2&a_0&a_1\\a_1&a_2&a_0\end{matrix}\right)=a_0I+a_1\Omega+a_2\Omega^2$

-------------本文结束-------------