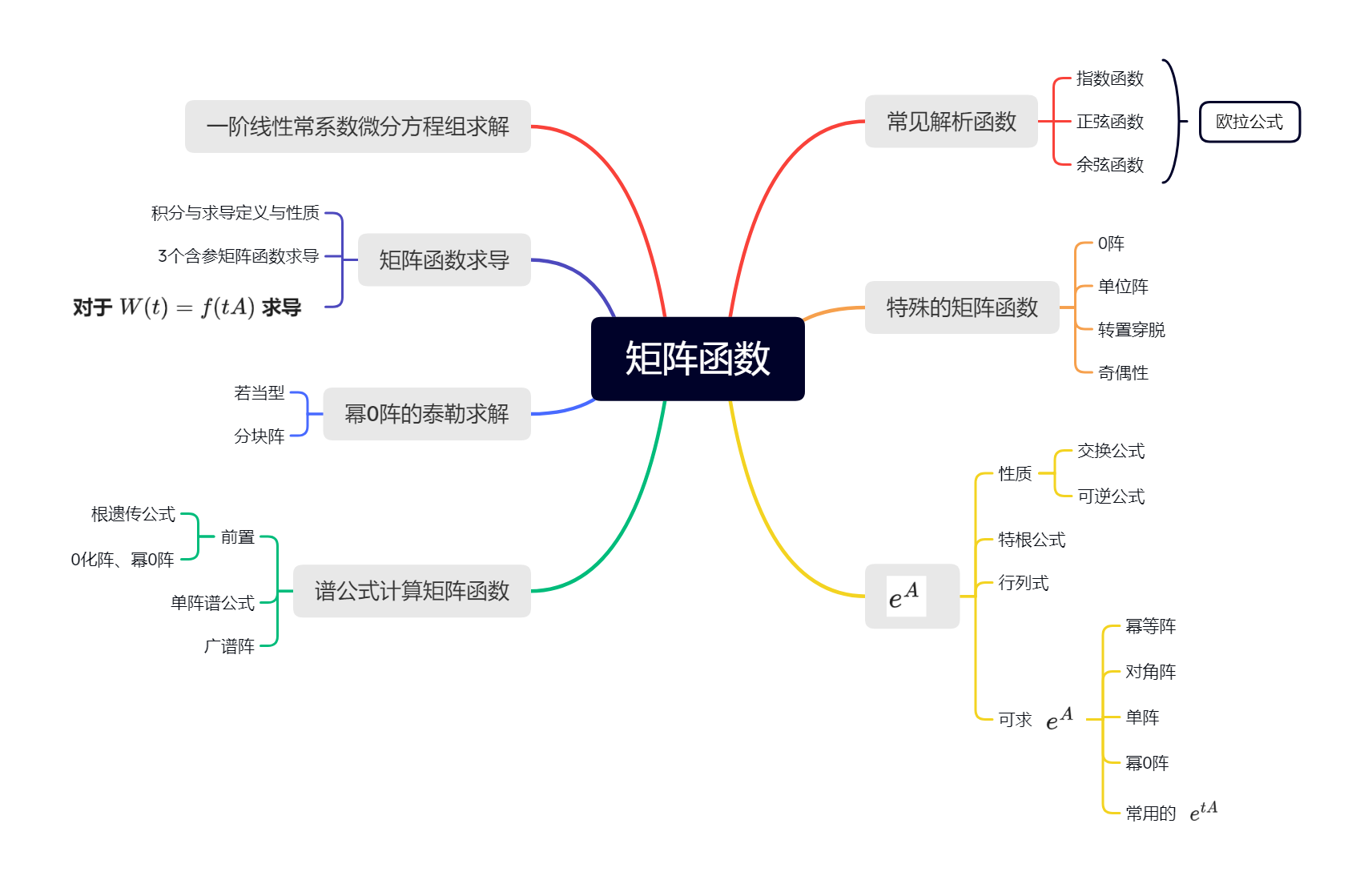
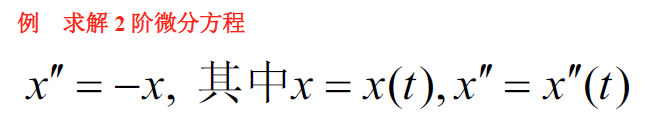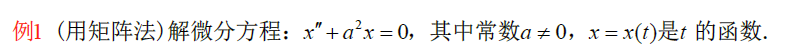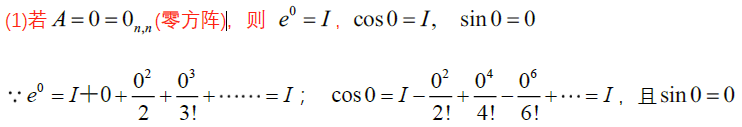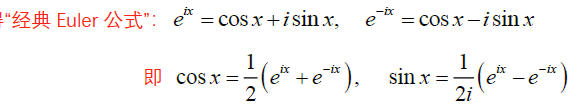矩阵函数
3.1 常见泰勒解析函数
3.1.1 指数函数

引入参数

3.1.2 正弦级数
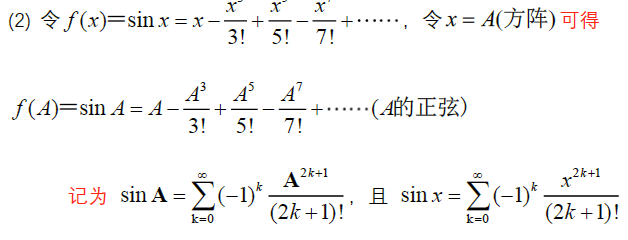
引入参数

3.1.3 余弦级数
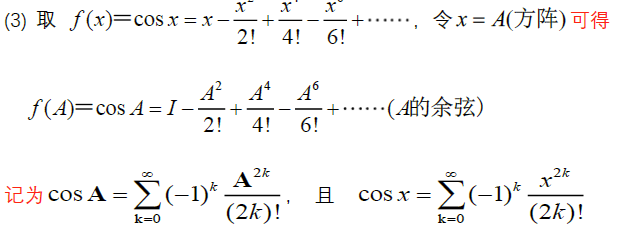
引入参数
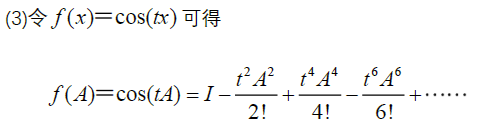
3.1.4 一些约定
a. A为0阵
b. 奇偶性
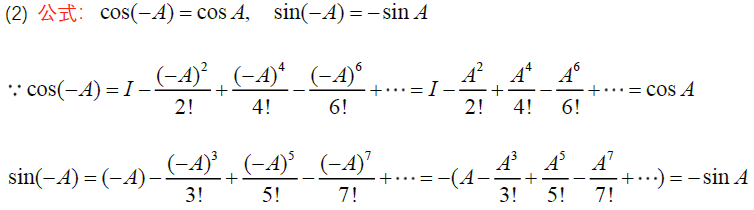
c. 单位阵
$e^{tI}=e^tI,sin(tI)=sin(t)I,cos(tI)=cos(t)I$
d. 转置穿脱
e. H阵
3.2 欧拉公式
$e^x$ 与 $cosx$ 和 $sinx$ 的关系
引入参数
3.3 $e^A$
3.3.1 $e^A$ 性质
a. 交换公式
若满足交换公式,则有
SP
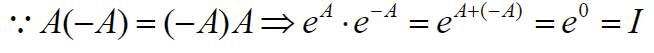
b. 可逆公式
任一方阵 $A$ 都有 $e^A$ 可逆,且 $(e^A)^{-1}=e^{-A}$
引入参数
$(e^{tA})^{-1}=e^{-tA}$ ,且 $e^{tA}e^{-tA}=I$
eg:证明 $sin^2A+cos^2A=I$
3.3.2 $e^A$ 特根公式
设方阵A特根 $\lambda(A)=\{\lambda_1,\cdots,\lambda_n\}$ ,则 $e^A$ 特根为 $\lambda(e^A)=\{e^{\lambda_1},e^{\lambda_2},\cdots,e^{\lambda_n}\}$
3.3.3 $e^A$ 行列式
3.3.4 一些特殊矩阵 $e^A$ 可求
a. 幂等阵
若 $A^2=A$ ,则有 $e^{tA}=I+(e^t-1)A$
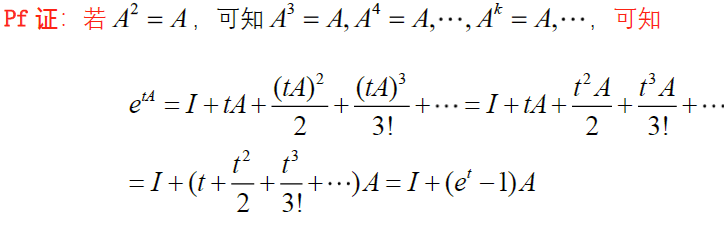
第一列与第二列每个元素绝对值差1的,很有可能是幂等阵
eg
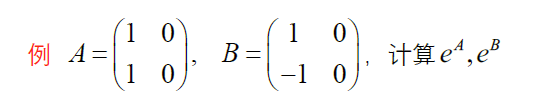
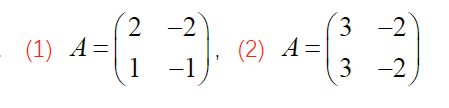
b. 对角阵
对角阵 $D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)$ ,则 $f(D)=\left(\begin{matrix}f(\lambda_1)&&\\&\ddots&\\&&f(\lambda_n)\end{matrix}\right)$
令函数 $f(x)=e^{tA}(t为参数)=\sum_{k=0}\limits^\infty\frac{(tx)^k}{k!}$ ,则 $f(D)=e^{tD}=\sum_{k=0}\limits^\infty\frac{(tD)^k}{k!}$
sp
eg
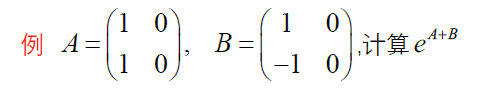
c. 单阵(谱公式)
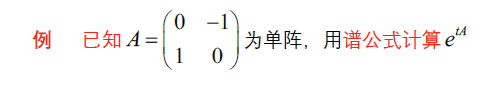
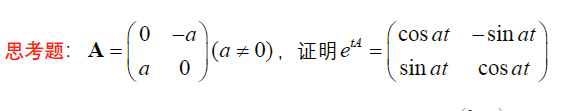

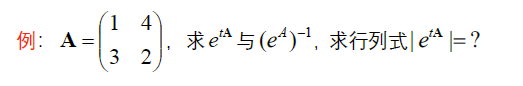
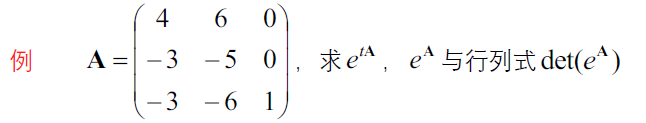
d. 幂0阵(泰勒公式)
$A^k=0$ ,则 $A$ 为幂0阵
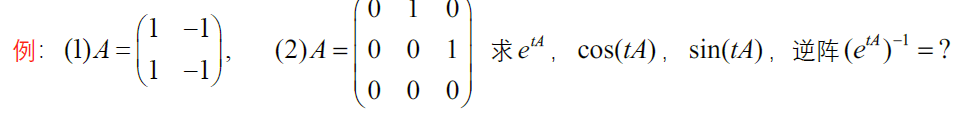

3.3.5 常用 $e^{tA}$
3.4 谱公式计算矩阵函数
3.4.1 前置知识
a. 根遗传公式
设 $n$ 阶方阵 $A$ 特根 $\lambda(A)=\{\lambda_1,\cdots,\lambda_n\}$ ,则 $f(A)$ 的特根为 $\lambda(f(A))=\{f(\lambda_1),\cdots,f(\lambda_n)\}$ ,其中 $\lambda(f(A))=\{f(\lambda_1),\cdots,f(\lambda_n)\}$ 为任意多项式函数,满足 $f(A)=c_0I+c_1A+c_2A^2+\cdots+c_kA^k$
b. 0化式、特根与幂0阵
0化式:若多项式 $f(x)$ 使 $f(A)=0$ ,称 $f(x)$ 为 $A$ 的0化式
- A的全体特根是任意0化式 $f(x)$ 的根 或 A的0化式 $f(x)$ 含有A的全体不同根
- sp :若 $A$ 为单阵,则0化式 $f(x)$ 不含重复根,即不含大于2的幂次项

若 $A^k=0(k\ge 2)$ 为幂0阵,则A的全体特根为 $\lambda(A)=\{0,\cdots,0\}$

若 $(A-aI)^k=0(k\ge 2)$ 为平移幂0阵,则A的全体根为 $\lambda(A)=\{a,\cdots,a\}$

3.4.2 单阵谱公式

3.4.3 广谱公式(非单阵2根2重)
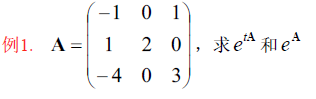

3.5 幂0与Taylor求解f(A)(最一般化求解)
若有 $A^k=0(k\ge 2)$ ,则 $f(x)$ 为任一解析式,则有
- 对于平移幂0阵 $(A-aI)^k=0(k\ge 2)$ ,$f(x)$ 为任一解析函数,则有公式 $f(A)=f(a)I+f’(a)(A-aI)+\frac{f’’(a)}{2!}(A-aI)^2+\cdots+\frac{f(a)^{k-1}}{(k-1)!}(A-aI)^{k-1}$
eg
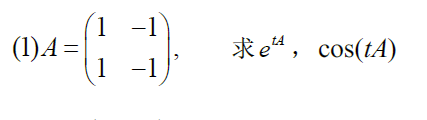


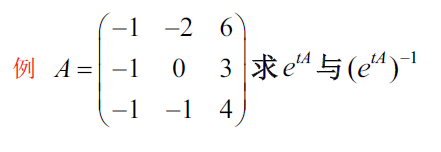
3.5.1 若当阵的矩阵函数
a. 若当阵
对于n阶0根若当阵,有
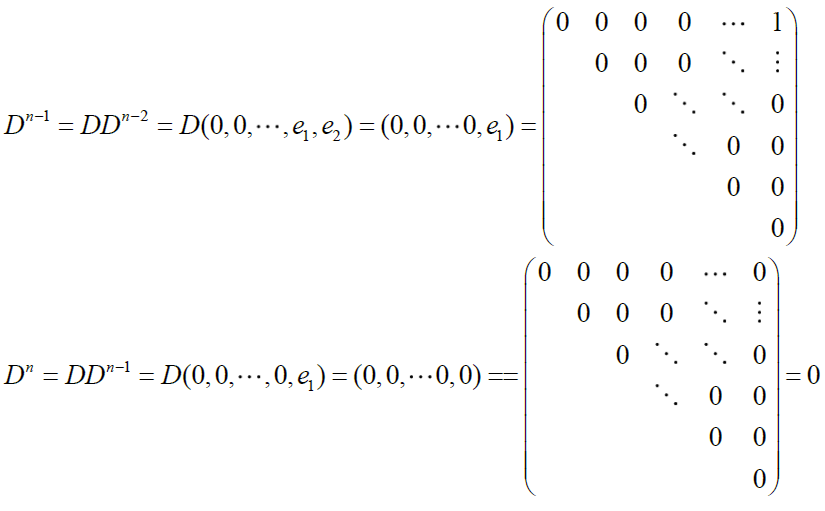
b. n阶若当阵的矩阵函数
对于n阶若当阵 $\left(\begin{matrix}a&1&&&0\\&a&1&&\\&&\ddots&\ddots&\\&&&\ddots&1\\&&&&a\end{matrix}\right)$ ,对任一解析函数 $f(x)$ 有
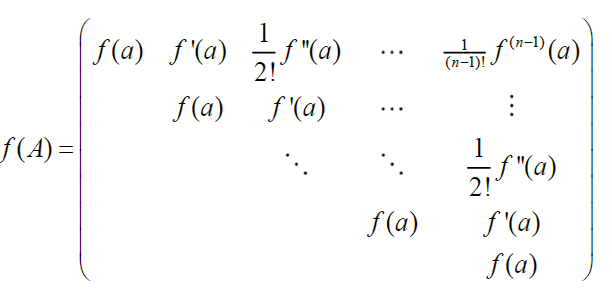

eg

3.5.2 分块阵

eg



3.6 矩阵函数求导
3.6.1 积分与求导定义
设 $m\times n$ 阶矩阵 $A(x)=\left(a_{ij}(x)\right)_{m\times n}$ 中的元素都是 x 的可导函数,则 $A(x)$ 为关于 $x$ 的求导为:
设 $A(x)=\left(a_{ij}(x)\right)_{m\times n}$ 的元素在区间 $[a,b]$ 连续,在区间 $[a,b]$ 上的积分记为
eg

3.6.2 运算性质
若 $A’(x)=\frac{dA(x)}{dx}\equiv 0$ $\iff$ $A(x)=D(常数矩阵)$
求和求导:设 $A(x)=(a_{ij}(x))_{n\times n}$ ,$B(x)=(b_{ij}(x))_{n\times n}$ 在区间 $[a,b]$ 可到,则有 $\frac{d(A(x)+B(x))}{dx}=\frac{dA(x)}{dx}+\frac{dB(x)}{dx}=A’(x)+B’(x)$
乘积求导:
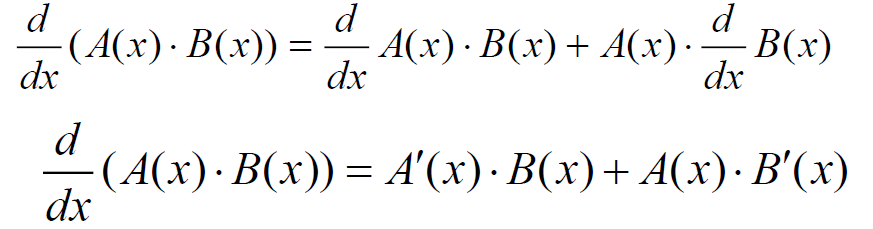
参数化:
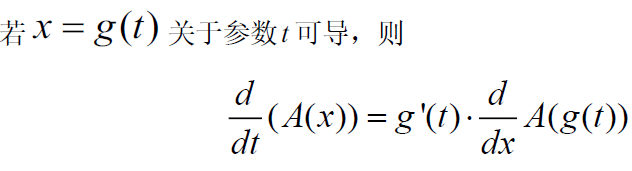
求和积分:
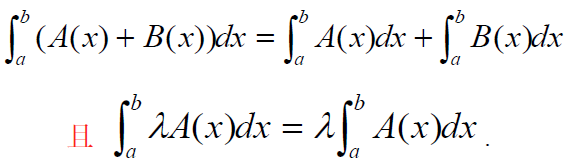
积分倍乘:
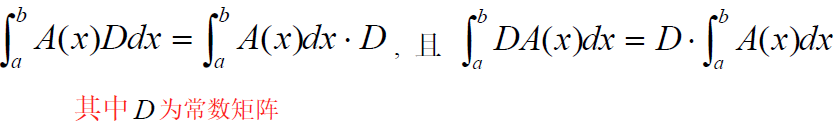
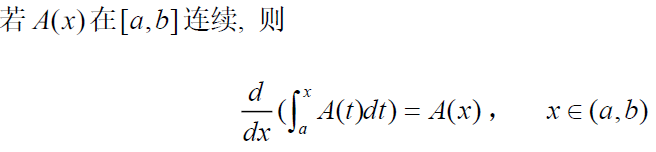
N-L公式

逆阵求导:
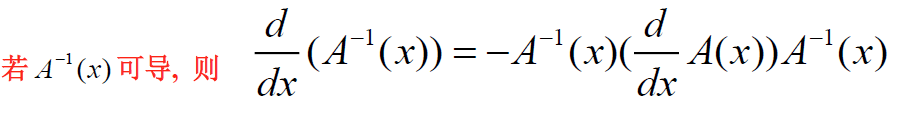
3.6.3 讨论含参阵的求导

3.6.4 3个含参矩阵函数的求导
对于三个矩阵函数 $f(tA)=e^{tA},cos(tA),sin(tA)$ ,设方阵 $A\in C^{n\times n}$ ,则有求导公式
SP
由欧拉公式
3.6.5 对于 $W(t)=f(tA)$ 求导
若已知 $W(t)=f(tA)$ ,两边求导 $\frac{df(tA)}{dt}=\frac{dW(t)}{dt}\Rightarrow W’(t)=Af’(tA)$
- 令 $t=0$ ,可得 $W’(0)=f’(0)A$
若 $W(t)=e^{tA}$ ,两边求导 $\frac{dW(t)}{dt}=\frac{d(e^{tA})}{dt} \Rightarrow W’(t)=Ae^{tA}$
- 令 $t=0$ ,可得 $W’(0)=A$
eg
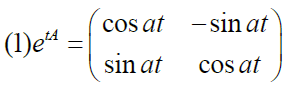
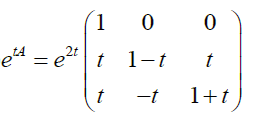
3.7 一阶线性常系数微分方程组
3.7.1 求解齐次方程组
a. 一阶微分
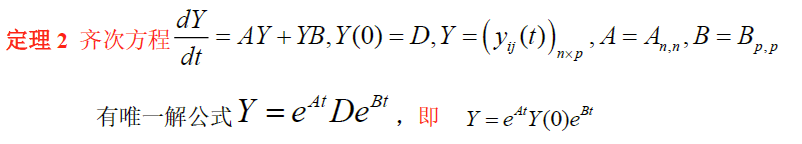
eg


二阶微分