5.查找 | AmosTian

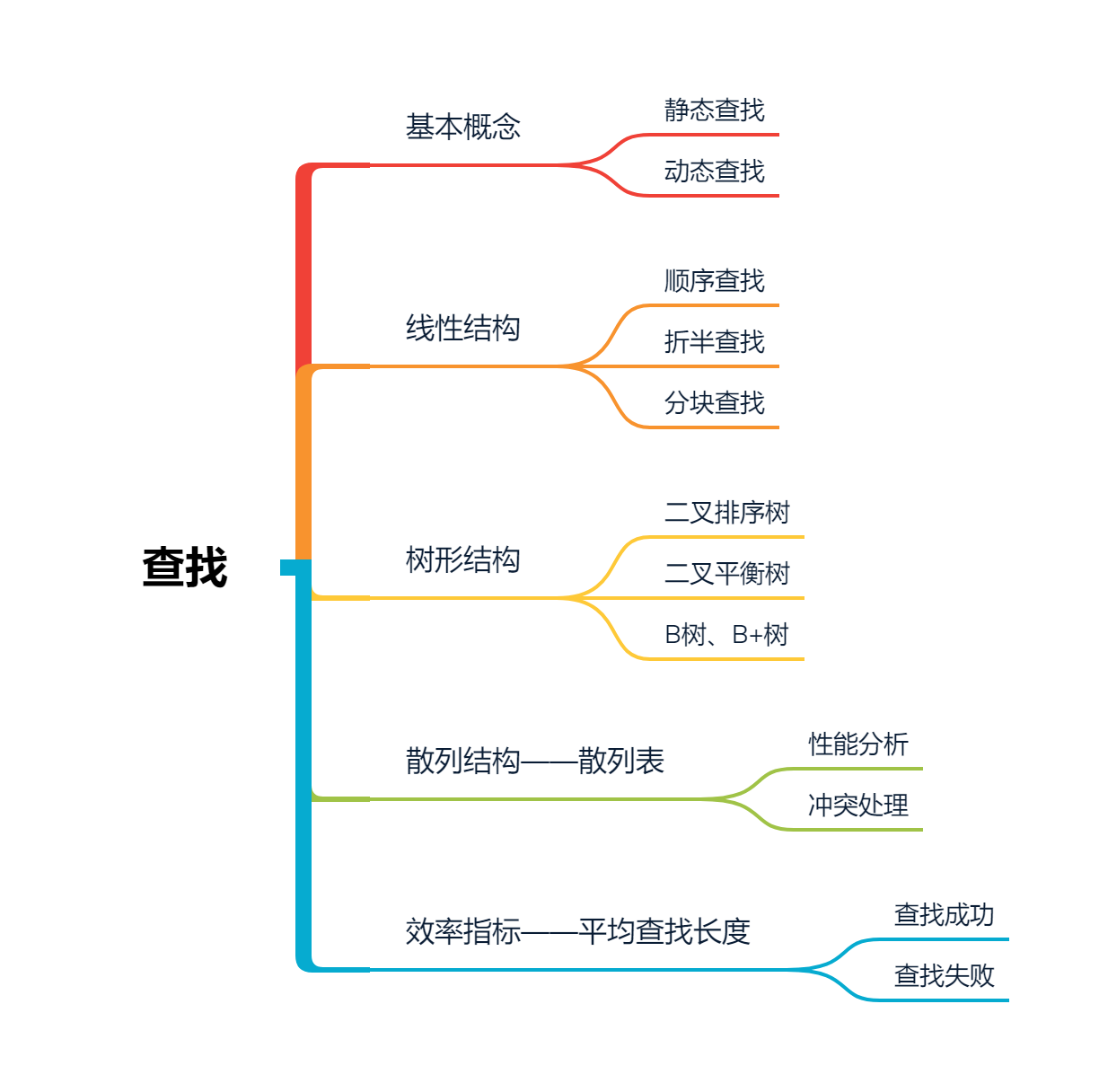
查找的概念与部分实现

## 5.1 基本概念 > 关键字：表示待查找元素的某个数据项的值 - 基于关键字的查找，查找结果是唯一的 > 查找：在数据集合中寻找满足条件的元素过程 > 查找表（查找结构）：用于查找的数据集合 - 四种操作查找特定数据元素是否在表中；检索满足条件的某个特定数据元素的各属性；在查找表中插入一个数据元素；从查找表中删除某个数据元素 > 静态查找表：无需动态地插入或删除的查找表称为动态查找表 - 顺序查找表 - 折半查找表 - 散列查找 > 动态查找表：需要动态删除和查找的查找表 - 二叉排序树的查找 - 二叉平衡树 - B树、B+树 - 散列查找 > 平均查找长度：所有查找过程中进行关键字的比较次数的平均值 $$ \begin{aligned} p_i表示查找第i个元素的概率，&c_i表示查找第i个元素所需进行的比较次数\\ &ASL=\sum_{i=1}^{n}p_ic_i\\ \end{aligned} $$

5.2 线性结构的查找

typedef struct{
	ElemType *elem;//存储空间基址，0号单元留空
    int TableLen;//表的长度
}SSTable;

5.2.1 顺序查找

存储结构：顺序表；链表
扫描所有查找表每个元素的方式
顺序表：下标递增
链表：next 指针域
哨兵的作用：SSTable.elem[0] 设为哨兵，不必检查数组是否越界，i=0 一定会跳出循环

1. 无序线性表的顺序查找

int Search_Sq(SSTable ST,KeyType key){
    i = ST.TableLen;
    ST.elem[0] = key;//设置哨兵
    while(ST.elem[i] != key) i--;
    return i;
}

$\begin{aligned} ASL_{成功}=\sum_{i=1}^{n}\frac{1}{n}(n-i-1)=\frac{n+1}{2}\\ ASL_{失败}=\sum_{i=1}^n\frac{n(n+1)}{n}=n+1 \end{aligned}$

优点

存储结构：顺序存储、链式存储
- 链式结构只能顺序查找
对数据的有序性无要求

缺点

效率低

2. 有序顺序表的顺序查找

int Search_Sq(SSTable ST,KeyType key){
    i = ST.length;
    ST.elem[0] = key;
    while(ST.elem[i] < key)	i--;
    if(key == ST.elem[i])	return i;
    return 0;
}

$\begin{aligned} ASL_{成功} = \sum_{i=1}^{n}\frac{1}{n}(n-i+1)=\frac{n+1}{2}\\ ASL_{不成功}=\sum_{i=1}^{n}q_il_i=\frac{1+2+...+n+n}{n+1}=\frac{n}{2}+\frac{n}{n+1} \end{aligned}$

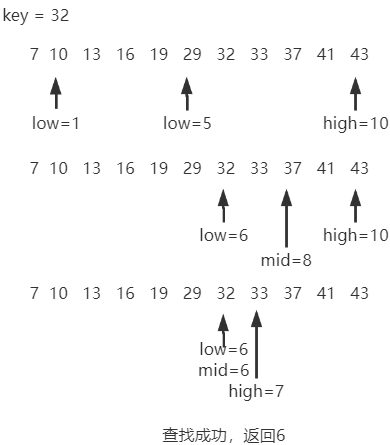
5.2.2 折半查找

适用情况：有序的顺序表

int Binary_Search(SSTable L,ElemType key){
    int low,high = L.TableLen-1,mid;
    while(low < high){
        mid = (low+high)/2;
        if(L.elem[mid]==key)
            return mid;//查找成功则返回所在位置
        else if(L.elem[mid] > key)
            high = mid-1;//从前半部分继续查找
        else
            low = mid + 1;//从后半部分继续查找
    }
    return -1;//查找失败，返回-1
}

查找失败

$\begin{aligned} ASL_{成功} = \frac{1*1+2*2+4*3+4*4}{11}=3\\ ASL_{失败}=\frac{3*4+4*8}{12}=\frac{11}{3} \end{aligned}$

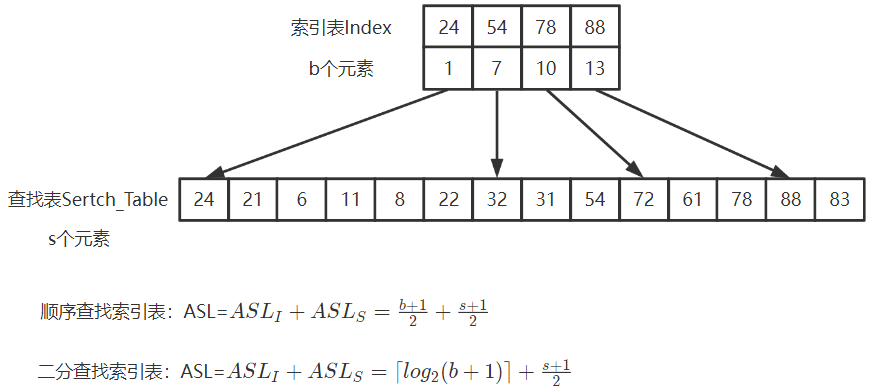
5.2.3 分块查找

将查找表分为若干块。块内无序，块间有序。
第一块最大关键字小于第二块最大关键字
索引表：索引表中存储每块的最大关键字和各块中的第一个关键字地址
索引表按关键字有序排列

分块查找步骤

索引表中查找待查记录所在块
顺序查找、折半查找索引表
块内顺序查找

5.3 树型结构的查找

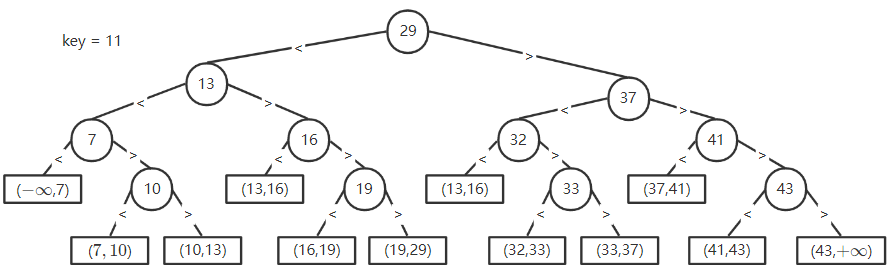
5.3.1 二叉排序树

typedef struct TreeNode{	
    ElementType key;	
    struct TreeNode *parent,*left,*right;
}Node, *BST;

p->lchild->data < p->data < p->rchild->data;

中序遍历可以得到有序序列

1. 构建

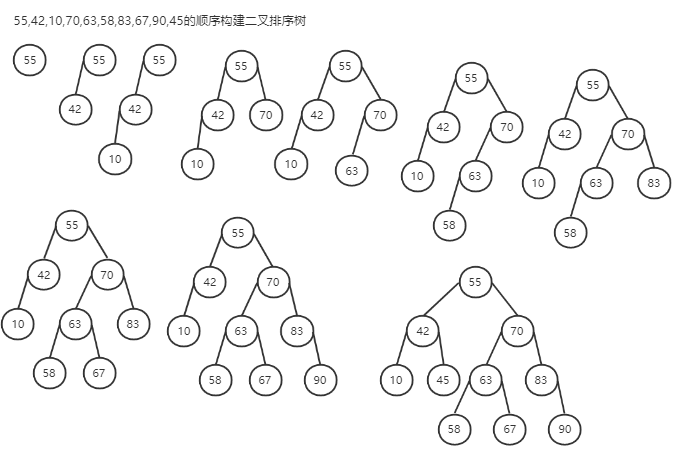
2. 查找

while(!T && key != T->data){
	if(key < T->data)
        T = T->lchild;
    else
        T = T->rchild;
}

一棵二叉排序树上的查找序列，第 n,n+1 个数不能分居第 n-1 个数的两侧如

3. BST插入

查找过程中，不存在目标结点，再插入

新插入的结点一定是一个叶结点，且是查找失败时，查找路径上访问的最后一个结点的孩子

void Insert(BST T,Node *p){	
    Node *x = T,*y = NULL;
    while(x != NULL){//查找目标结点		
        y = x;
        if(x->key > p->key)
            x = x->left;
        else
            x = x->right;
    }
    p->parent = y;
    if(y == NULL)//第一个结点	
        T = p;
    else if(y->key > p->key)//待插入结点值小于叶结点	
        y->left = p;	
    else//待插入结点值大于等于叶结点
        y->right = p;
}

4. BST删除

BST中元素间的相对位置与BST中序序列中元素间的相对位置相同

若删除结点 p 是叶结点，则直接删除
若删除结点 p 是某单支树，则用其孩子结点代替
若删除结点 p 有左右孩子
- 用直接后继 next 代替，p 的左孩子变为 next 的左孩子，p 的右孩子变为 next 的最右左子树
- 用直接前驱 pre 代替，p 的右孩子变为 pre 的右孩子，p 的左孩子变为 pre 的最左右子树

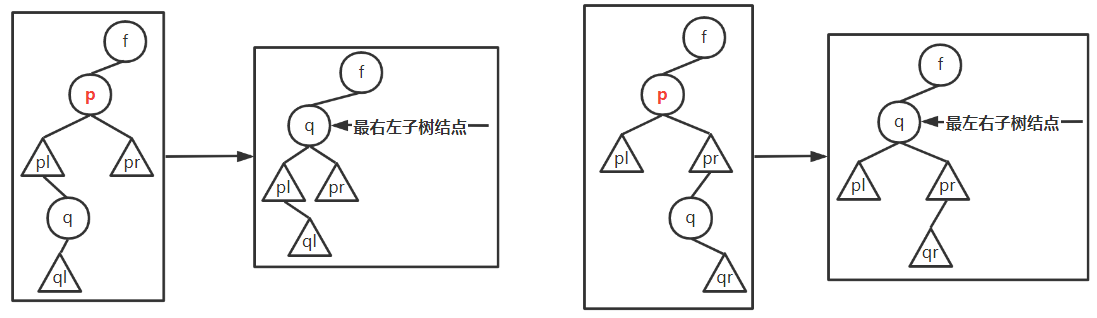
void Transplant(BST T, Node *x, Node *y){// y替换x的位置
    if(x->parent == NULL)
        T = y;
    else if(x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;
    if(y != NULL)
        y->parent = x->parent;
}

void Delete(BST T, Node *p){
    if(p->left == NULL)//p左子树空，则用其右孩子根结点代替p的位置
        Transplant(T, p, p->right);
    else if(p->right == NULL)//p的右子树为空，用其左孩子代替p的位置
        Transplant(T, p, p->left);
    else{//按上图第二种情况写，第一种类推
        Node *q = FindMin(p->right); //找p的最左右子树结点		
        
        
        if (q->parent != p){
            Transplant(T, q, q->right);
            q->right = p->right;
            q->right->parent = q;
        }
        Transplant(T, p, q);
        q->left = p->left;
        q->left->parent = q;
    }
}

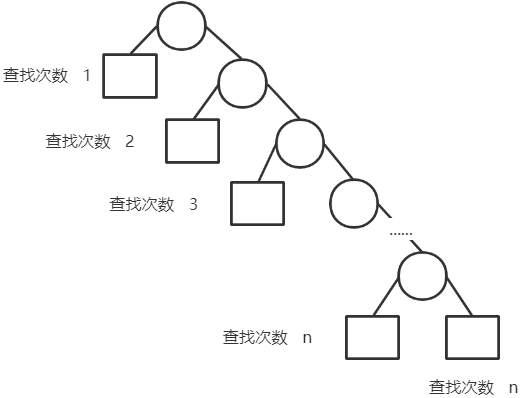
5. BST平均查找长度

计算

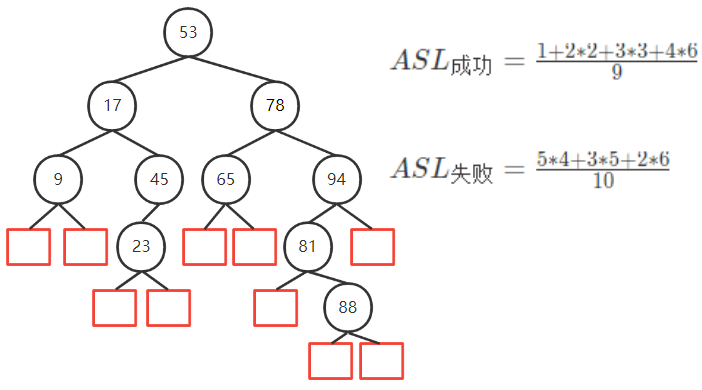
查找失败的情况相当于将 $(-\infty,+\infty)$ 用n个数分为 n+1 个区间

最好情况 ASL = $O(logn)$ 平衡二叉树

最坏情况 ASL = $O(n)$ 单链表

6. 二分查找与二叉排序树

ASL相同
- 二分查找判定树唯一
- BST是动态树，不唯一
  插入顺序不同，生成的BST不同

2. 区别 | | 类型 | 存储结构 | 构建时间复杂度 | | -------- | ---------- | ---------- | -------------- | | 二分查找 | 静态查找表 | 有序顺序表 | $O(n)$ | | BST | 动态查找表 | 修改指针 | $O(log_2n)$ | ### 5.3.2 平衡二叉树 > 见 3-树.pdf \3.2.6 二叉树的应用\2. 平衡二叉树 ### 5.3.3 B树 > 多路平衡查找树 #### 1. 特点 1. 每个结点最多 $m-1$ 个关键字，最少 $\lceil \frac{m}{2} \rceil-1 $ 个关键字，即每个结点最少$\lceil \frac{m}{2} \rceil$ 个分叉 m阶B树为m叉树如：5叉B树，每个结点最多有4个关键字，最少有2个关键字 2. 任一结点，其子树高度必须相等 - 所有查找失败结点作为叶子结点出现在同一层，并且不带任何信息 - n个关键字必有 n+1 个叶子结点在区间 $(-\infty,+\infty)$ 间插入 n 个数据，分为 n+1 个查找失败区间，即有 n+1 个叶子结点 3. 非叶结点关键字有序 $k_1

n个结点的B树高度

最小高度
每个结点尽可能满 m-1 个关键字，m个分叉
$(m-1)(1+m+m^2+…+m^{h-1})=(m-1)\frac{1-m^h}{1-m}=m^h-1 \Longrightarrow h\ge log_m(n+1)$
最大高度
各层分叉尽可能少，除第一二层其他层结点 $\lceil \frac{m}{2} \rceil$
$\begin{cases} &第一层 &1\\ &第二层&2\\ &第三层&2\lceil \frac{m}{2} \rceil\\ &...\\ &第h层&2\lceil \frac{m}{2} \rceil^{h-2} \\ &叶子层&2\lceil \frac{m}{2} \rceil^{h-1}\\ &第h+1层&n+1 \ge 2\lceil \frac{m}{2} \rceil^{h-1} \Longrightarrow h\le log_{\lceil \frac{m}{2} \rceil} \frac{n+1}{2}+1 \end{cases}$

2. 基本操作

插入

要求

除根结点，每个结点关键字个数 $\lceil \frac{m}{2} \rceil -1 \le n \le m-1$
$子树0上的关键字 <k_1 < k_2 < … < k_{m-1}<子树1上的关键字$

步骤

新元素插入后在最底层 “终端结点”，动态确定插入位置
插入结点后，若 $结点关键字个数 > m-1$ ，则从中间位置 $\lceil \frac{m}{2} \rceil$ 处分裂为两部分
$\lceil \frac{m}{2} \rceil$ 右面部分形成一个新结点
$\lceil \frac{m}{2} \rceil$ 处关键字加入父结点的关键字，若此行为造成父结点关键字个数 > m-1，则父结点继续分裂，B树高度加一

删除

对非终端结点关键字删除必可转化为对终端结点的删除
$替换原关键字 \begin{cases} 直接前驱:左子树最右下\\ 直接后继:右子树最左下 \end{cases}$
删除后，本结点关键字个数不够 $\lceil \frac{m}{2} \rceil$
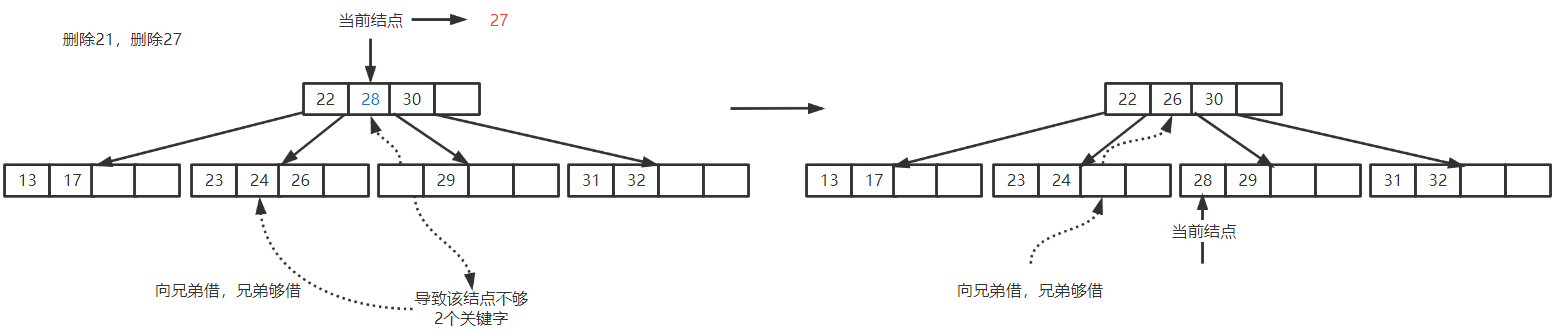
$\begin{cases} 借右兄弟&用直接后继填补空缺\\ 借左兄弟&用直接前驱填补空缺 \end{cases}$
兄弟不够借
$当前结点与左(或右)兄弟及夹在中间的双亲结点关键字合并$

5.3.4 B+树

m叉B+树最多m个子树，m个结点最多m+1个

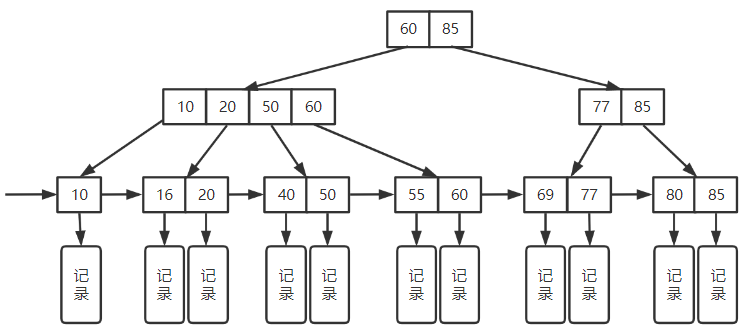
1. 特点

每个分支结点最多 m 个子树
m叉B+树m个子树，每个结点有m个关键字
非叶根结点，至少有两棵子树，其余分支结点有 $\lceil \frac{m}{2} \rceil$ 个子树
所有叶结点包含全部关键字及指向相应记录的指针
相邻叶结点按关键字大小顺序排列
所有非叶分支结点仅包含其子结点的最大关键字值及指针(指向叶结点)

2. 查找

无论查找成功失败，都走到最下一层叶结点

分块查找
按叶结点顺序查找

3. B+树与文件系统关系

索引块以块为单位存放在磁盘，内存每次以块为单位读写
树越高，读/写 IO次数越多，速度越慢
尽可能使文件系统的树矮，使每个结点包含更多结点

5.3.5 B树与B+树的对比

B树	B+树[分块查找]
m个关键字m+1棵子树	m个关键字m棵子树
根结点关键字数 $n\in [1,m-1]$ 其他结点 $n \in [\lceil \frac{m}{2} \rceil-1,m-1]$	根结点关键字数 $n \in [1,m]$ 其他结点 $n \in [\lceil \frac{m}{2} \rceil ,m ]$
叶结点都在同一层，表示查找失败结点	叶包含所有关键字
各结点关键字不重复，每个结点都含记录存储地址	非叶结点关键字是叶结点关键字副本，非叶结点仅起索引作用，指针指向含该最大值的子树

5.4 散列结构的查找

5.4.1 基本概念

散列表：建立关键字和存储地址之间的一种直接映射关系

散列函数：把查找表中的关键字映射为该关键字逻辑地址的函数

Addr = Hash(key)

冲突：一个散列函数会把多个关键字映射到同一地址上

同义词：发生碰撞的不同关键字为同义词

5.4.2 散列函数的构造

1. 直接定址法

$H(key) = key$ 或 $H(key) = a*key+b$

适用于关键字基本连续

2. 除留取余法

$H(key)=key\%p$

m 为散列表长，p为不大于m的最大质数

3. 数字分析法

关键字是r进制数，r个数码在各数位上出现的频率不同，故选取数码分布较均匀的位作为散列地址

适合已知的关键字集合

4. 平方取中法

取关键字的平方值的中间几位作为散列地址

散列地址与关键字的每位都有关，因此散列地址分布比较均匀

5.4.3 处理冲突的方法

1. 开放定址法

$H_i=(H(key)+d_i)\%m$

线性探测法
$d_i=1,2,…,k(k \le m-1)$
造成同义词聚集在相邻的散列地址，大大降低查找效率
平方探测法
$d_i=0^2,1^2,-1^2,2^2,-2^2,…,k^2,-k^2(k\le \frac{m}{2})$
m必须是一个可以表示为 4k+3 的素数
- 避免出现堆积问题
- 不能探测散列表所有单元，但至少探测一半
再散列法
$H_i = (H(key)+i*Hash_2(key))\%m$
$初始探测位置H_0=H(key)\%m$ ，i是冲突次数，初始为0
最多经历 m-1 次探测就会遍历表中所有位置，回到 $H_0$
伪随机数法
$d_i=伪随机数序列$

2. 拉链法

同义词以链表形式链接到同一单元后

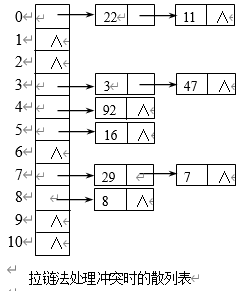
5.4.4 散列查找和性能分析

1. 平均查找长度

开放定址法

$\begin{cases} & ASL_{成功}=\frac{1}{元素个数n}\sum_{i=1}^n查找a_i的长度\\ &ASL_{失败}=\frac{1}{除数+1}\sum_{i=1}^{n}a_i距其右方第一个空位长度 \end{cases}$

拉链法

$\begin{cases} ASL_{成功}=\frac{1}{元素个数n}\sum_{i=1}^{n}a_i到表头距离\\ ASL_{失败}=\frac{1}{除数+1}\sum_{i=1}^{n}a_i到表尾距离 \end{cases}$

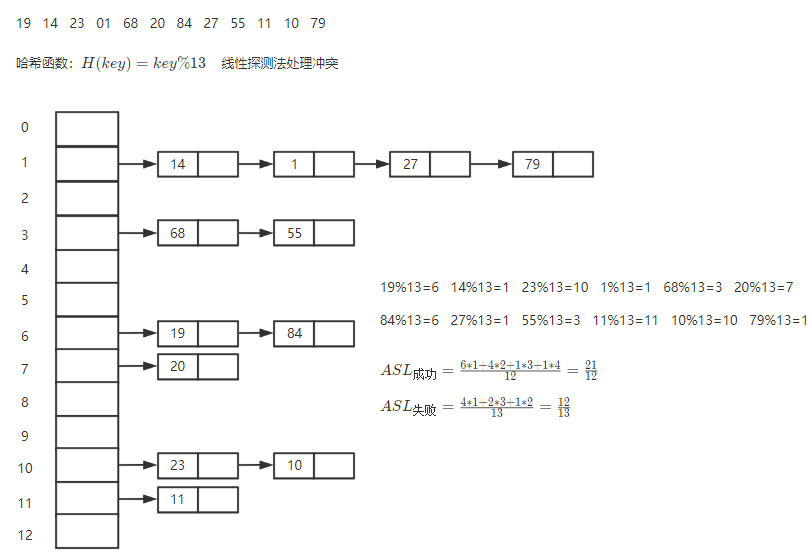
2. 性能分析

装填因子

$\begin{aligned} 装填因子\alpha=\frac{n}{m}=\frac{已装入元素个数}{哈希表长}\\ ASL=\frac{1}{2}(1+\frac{1}{1-\alpha}) \end{aligned}$

装填因子相关因素：散列函数、冲突解决策略、装填因子
平均查找长度与 $\alpha$ 直接相关，不与表中元素数相关

3. 散列表删除某个元素

拉链法：物理删除

开放定址法：待删除位置打标记

查找时遇到标记为删除的地址，表示查找失败