AmosTian

0%

2+3.线性模型与全连接前馈神经网络

发表于 更新于 分类于 > >
本文字数 16.5k字 | 阅读时长 ≈ 50 分钟

[TOC]

updated1: 2024-03-19 16:22:59

2. 线性模型

线性模型可以看做单层神经网络

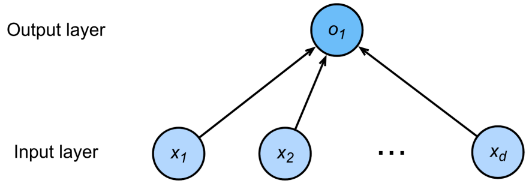
image-20240316230758952

torch中创建的向量为行向量，所以后续基于行向量进行原理推导

对于 线性模型，$d$ 维行输入向量 $\mathbf{x}=[x^{(1)},x^{(2)},\cdots,x^{(d)}]\in \mathbb{R}^{1\times d}$ ，输出 $\hat{y}$ 是输入的加权和

$\mathbf{w}=[w_1,w_2,\cdots,w_d]\in \mathbb{R}^{1\times d}$

衡量预测质量：比较真实值和预测值，假设 $y$ 是真实值，$\hat{y}$ 是预测值，可以使用平方损失衡量预测质量

对于参数的取值，需要收集一些数据点来决定，称为训练数据，通常越多越好。假设有 $n$ 个样本，数据集为

定义损失函数：将模型对数据的预测结果与真实结果误差作为损失函数，希望这个损失越小越好

所以目标函数为：最小化损失函数来学习参数

使用训练数据进行 参数学习 ：通过梯度下降法更新参数使损失函数的最小

为简化过程，将偏差加入权重，$\mathbf{w}=[w_1,w_2,\cdots,w_d,b]$ ，对数据进行1扩充，$\mathbf{x}_i=[x_i^{(1)},x^{(2)}_i,\cdots,x^{(d)}_i,1]$

则有，

损失函数为

对参数求梯度

由于该函数是凸函数，最优解为

2.1 线性回归实现

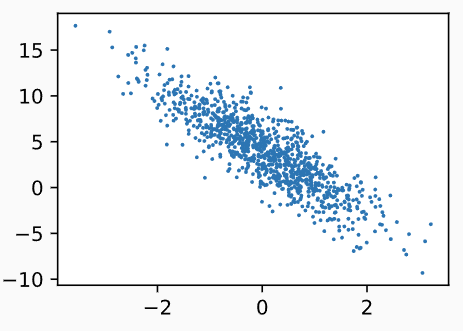
2.1.1 生成数据

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
%matplotlib inline #在jupyter notebook中显示图像
import random
import torch
from d2l import torch as d2l

#功能：根据真实的参数，基于线性模型生成带噪音的随机训练数据
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    #生成训练集矩阵，n*|w|，从正态分布N(0,1)中抽取输入值
    #	n行表示n个数据，|w| 列表示一个数据有|w|个特征
    X = torch.normal(0, 1, (num_examples, len(w)))
    # y是n维真实输出向量
    y = torch.matmul(X, w) + b
    #在真实输出上加噪音，噪音服从N(0,0.01)
    y += torch.normal(0, 0.01, y.shape)
    #y的行数无所谓，列数指定
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
# features中的每一行都包含一个二维数据样本
# labels中的每一行都包含一维标签值
features, labels = synthetic_data(true_w, true_b, 1000)
print('features:', features[0],'\nlabel:', labels[0])
# features: tensor([0.2151, 0.0915])
# label: tensor([4.3277])

# 生成第二个特征features[:, 1]和labels的散点图
d2l.set_figsize()

# plt.scatter(x,y) xxx.detach()，从计算图中分离出来才能转为numpy的ndarray
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1)

image-20240317110949088

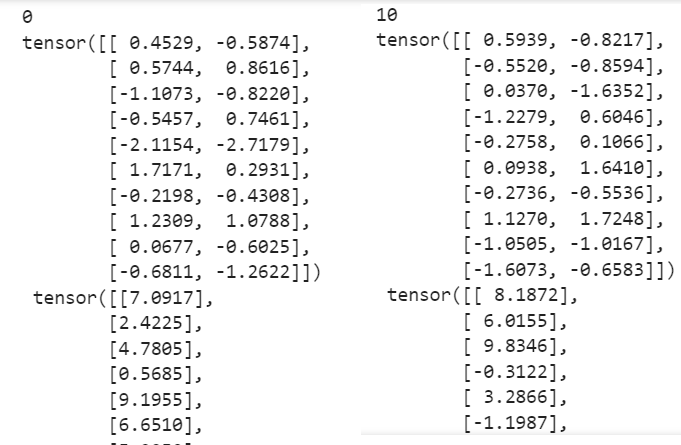
2.1.2 生成批量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
batch_size = 10

#输入：批量大小、整体数据集，
#输出：指定大小的批量集
def data_iter(batch_size, features, labels):
    #数据数为特征数
    num_examples = len(features)
    #为输入数据的索引创建列表
    indices = list(range(num_examples))
    # 对索引列表随机排序
    random.shuffle(indices)
    #功能：数据每隔一个批量封装为可迭代对象的一项，这些批量项被封装为一个可迭代对象作为函数返回值
    # range(start,end,step)从start到end间隔step-1个数取一个数
    for i in range(0, num_examples, batch_size):
        print(i)
        #从乱序索引列表中中逐次选择批量
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        # yield会将返回值封装为可迭代对象的一个item，item有两个,可用X,y解构可得feature[]与label
        #	yield一次，主调函数接收一次
        yield features[batch_indices], labels[batch_indices]

#yield一次，主函数就会接收一次，即 data_iter中for循环的 i 会被记录(0,10,20,...990)
#返回100个批量，每个批量10个数据
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

image-20240317145453732

2.1.3 初始化模型

模型定义

1
2
3
def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

随机初始化参数

1
2
3
4
#随机初始化参数
# 从 N(0,0.01)的正态分布中采样，2*1的列向量，反向传播时，该tensor就会自动求导
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

更新这些参数，直到这些参数足够拟合训练数据。每次更新都需要计算损失函数关于模型参数的梯度，requires_grad=True 对这个参数引入自动微分计算梯度

2.1.4 定义损失函数

1
2
3
def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

2.1.5 定义优化算法

若损失函数计算的是整个样本集上的损失

其梯度为

若采用小批量随机梯度下降法，用 $\vert \mathcal{B}\vert$ 个样本的小批量样本集 $\mathcal{B}$

沿着负梯度方向更新参数，每步更新的步长由学习率 lr 决定

1
2
3
4
5
6
7
8
def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    #param是由参数迭代而来，param默认会继承参数的自动微分，
    #	而更新后的param不需要计算其梯度，所以torch.no_grad()
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

  • 若一个节点（叶子变量：自己创建的tensor）requires_grad被设置为True，那么所有依赖它的节点requires_grad都为True

  • 当requires_grad设置为False时，反向传播时就不会自动求导了，因此大大节约了显存或内存

    with torch.no_grad 起到了截断自动微分的作用，对不需要计算微分的部分进行截断

2.1.6 训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
'''1.生成数据'''
import random
import torch
from d2l import torch as d2l

# 功能：根据真实的参数，基于线性模型生成带噪音的随机训练数据
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    #生成训练集矩阵，n*|w|，从正态分布N(0,1)中抽取输入值
    #	n行表示n个数据，|w| 列表示一个数据有|w|个特征
    X = torch.normal(0, 1, (num_examples, len(w)))
    # y是n维真实输出向量
    y = torch.matmul(X, w) + b
    #在真实输出上加噪音，噪音服从N(0,0.01)
    y += torch.normal(0, 0.01, y.shape)
    #y的行数无所谓，列数指定
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
# features中的每一行都包含一个二维数据样本
# labels中的每一行都包含一维标签值
features, labels = synthetic_data(true_w, true_b, 1000)

'''2. 模块定义'''
'''2.1 小批量生成模块'''

batch_size = 10
#输入：批量大小、整体数据集，
#输出：指定大小的批量集
def data_iter(batch_size, features, labels):
    #数据数为特征数
    num_examples = len(features)
    #为输入数据的索引创建列表
    indices = list(range(num_examples))
    # 对索引列表随机排序
    random.shuffle(indices)
    #功能：数据每隔一个批量封装为可迭代对象的一项，这些批量项被封装为一个可迭代对象作为函数返回值
    # range(start,end,step)从start到end间隔step-1个数取一个数
    for i in range(0, num_examples, batch_size):
        print(i)
        #从乱序索引列表中中逐次选择批量
        batch_indices = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        # yield会将返回值封装为可迭代对象的一个item，item有两个,可用X,y解构可得feature[]与label
        #	yield一次，主调函数接收一次
        yield features[batch_indices], labels[batch_indices]

        
'''2.2 模型定义:线性回归模型'''
def linreg(X, w, b):  #@save
    return torch.matmul(X, w) + b

'''2.3 损失函数定义:均方损失'''
def squared_loss(y_hat, y):  #@save
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

'''2.4 随机梯度下降'''
def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    #param是由参数迭代而来，param默认会继承参数的自动微分，
    #而更新后的param不需要计算其梯度，所以torch.no_grad()
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()
    
'''3. 初始化超参数'''
lr = 0.03
num_epochs = 3
batch_size = 10

'''4. 开始训练'''
#随机初始化参数
# 从 N(0,0.01)的正态分布中采样，2*1的列向量，反向传播时，该tensor就会自动求导
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

#在训练集上进行三轮训练
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):  
        # hat_y是2维列向量。l为小批量平方损失向量
        l = squared_loss(linreg(X, w, b), y)
        # 对同一批量的平方损失求和，并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        #计算本轮迭代后的损失
        train_l = squared_loss(linreg(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
        
'''5. 对比真实参数'''
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')

2.2 基于pytorch实现线性回归

2.2.1 生成数据

1
2
3
4
5
6
7
8
9
import numpy as np
import torch
# torch.utils 是torch中的一个数据处理包
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

2.2.2 数据迭代器(理解)

1
2
3
4
5
6
7
8
9
10
11
def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    #将torch张量类型的数据集转换为torch中的张量数据集类型TensorDataset
    dataset = data.TensorDataset(*data_arrays)
    #shuffle：打乱数据集
    # 按批量大小从数据集中返回小批量数据，并将这些数据封装为Pytorch迭代器
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
# data_iter是Pytorch迭代器对象
data_iter = load_array((features, labels), batch_size)

在 data.DataLoader() 创建的迭代器对象中，封装了数据元组

  • 将整个数据集按批量大小划分为多个批量，并返回划分后的 可迭代对象

  • 可迭代对象可视为一个列表，列表的每一项封装了一个批量(元组)，对一个项操作，相当于对一个批量的操作

  • 遍历可迭代对象，相当于逐批量获取数据

为查看迭代器内容，需要使用 iter() 构造器将 Pytorch迭代器转换为 Python迭代器，然后使用 next(itr) 获取第一项

1
2
next(iter(data_iter))
print("第一批量的数据:\n",next(iter(data_iter)))

2.2.3 初始化模型

模型定义

对于标准深度学习模型，我们可以使用框架预定义好的层。每一层都可以理解为带有输入和输出的模型

使用框架之后，我们只需关注使用哪些层来构造模型，而不必关注层的实现细节。

  • 这种情况类似于为自己的博客从零开始编写网页。也能使用博客框架，博客框架环境配置好后，只需要关注博客内容即可

在Pytorch中，定义一个模型变量 net ，net 是一个 Sequential 类

  • Sequential 将多个层串联在一起。当给定输入数据时，模型变量将数据传入到第一层，第一层的输出作为第二层的输入，以此类推
1
2
3
4
5
# nn是神经网络的缩写
from torch import nn

#nn.Linear(输入向量维度,输出向量维度)
net = nn.Sequential(nn.Linear(2, 1))

随机初始化模型参数

1
2
3
4
5
6
7
8
9
10
#线性模型可以视为单层神经网络，在框架中只有第一层
#net[0].weight.data指定线性层的权重；
#	.normal_(means,var)，从均值为mean方差为var的正态分布中挑选初始值
#net[0].bias.data指定线性层的偏置
#	.fill_(x)，用x填充
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

for i in net.parameters():
    print(i)

Sequential 实例的 parameters() 函数可以获取当前层的参数，返回的是参数的迭代对象

1
2
3
4
Parameter containing:
tensor([[ 0.0059, -0.0101]], requires_grad=True)
Parameter containing:
tensor([0.], requires_grad=True)

2.2.4 损失函数

在nn模块中，定义了各种损失函数

均方损失，MSELoss 类

1
2
# 损失实例已经包含批量大小信息
loss = nn.MSELoss()

2.2.5 定义优化函数

PyTorch在优化模块 optim 中实现了随机梯度下降算法(SGD)的许多变种

使用SGD实例时，要指定优化的参数

  • 小批量SGD只需要指定学习率
1
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

2.2.6 训练过程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
import numpy as np
import torch
# torch.utils 是torch中的一个数据处理包
from torch.utils import data
from d2l import torch as d2l

#生成训练数据
def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    #生成训练集矩阵，n*|w|，从正态分布N(0,1)中抽取输入值
    #	n行表示n个数据，|w| 列表示一个数据有|w|个特征
    X = torch.normal(0, 1, (num_examples, len(w)))
    # y是n维真实输出向量
    y = torch.matmul(X, w) + b
    #在真实输出上加噪音，噪音服从N(0,0.01)
    y += torch.normal(0, 0.01, y.shape)
    #y的行数无所谓，列数指定
    return X, y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    #将torch张量类型的数据集转换为torch中的张量数据集类型TensorDataset
    dataset = data.TensorDataset(*data_arrays)
    #shuffle：打乱数据集
    # 按批量大小从数据集中返回小批量数据，并将这些数据封装为Pytorch迭代器
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
# data_iter是Pytorch迭代器对象
data_iter = load_array((features, labels), batch_size)

# nn是神经网络的缩写
from torch import nn

#nn.Linear(输入向量维度,输出向量维度)
net = nn.Sequential(nn.Linear(2, 1))
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

#定义损失函数
loss = nn.MSELoss()
#定义参数损失函数的优化算法
trainer = torch.optim.SGD(net.parameters(), lr=0.03) 

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        #对每个输入计算平方损失函数
        # 	l中已经包含了批量大小信息
        l = loss(net(X) ,y)
        #对参数的梯度置0
        trainer.zero_grad()
        #对损失函数反向传播计算梯度并求和
        l.backward()
        #参数更新一次
        trainer.step()
    #计算本轮迭代更新参数后的误差
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

2.3 softmax回归

回归任务：估计连续值

分类任务：预测一个离散的类别

  • 手写数字识别-10类
  • ImageNet：1000000张图片的，1000类自然物体分类
  • Kaggle上的分类问题：
    • 人类蛋白质显微镜图片28类
    • 恶意软件分类9类
    • WIkipedia评论分为7类

回归任务到分类任务

回归任务分类任务
单连续数值输出多离散输出
自然区间 $\mathbb{R}$输出 $p(i)$ 是预测为第 $i$ 类的置信度
与真实值的差作为损失
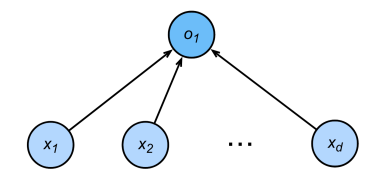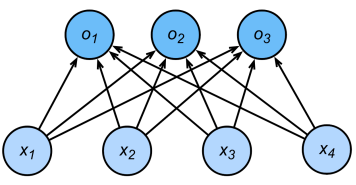image-20240317211949271image-20240317212003378

对类别编码，若有 $K$ 个类别，使用one-hot向量对真实样本 $(\mathbf{x}_i,y_i)$ 进行编码 $\mathbf{y}_i=[y_i^{(1)},y_i^{(2)},\cdots,y_i^{(K)}]$，令 $\kappa$ 为 $\mathbf{x}_i$ 的真实类别，则 $y_i^{(k)}=\begin{cases}1&,k=\kappa\\0&,k\neq \kappa\end{cases},k=1,\cdots,K$ ，样本 $\mathbf{x}_i$ 的真实类别 $y_i^{(k)}$ 服从一个分布 $p$

$\hat{y}_i^{(k)}=q(\hat{y}_i=k\vert \mathbf{x}_i)=softmax(o_i^{(k)})=\frac{e^{o_i^{(k)}}}{\sum\limits_{k=1}^Ke^{o_i^{(k)}}}=\frac{e^{\mathbf{x}_i\mathbf{w}_k^T}}{\sum\limits_{k=1}^Ke^{\mathbf{x}_i\mathbf{w}_k^T}}$ 表示将样本 $\mathbf{x}_i$ 预测为 $k$ 类的置信度，对样本 $\mathbf{x}_i$ 的类别预测置信度服从分布 $q$

  • $o_i^{(k)}=\mathbf{w}^T_k\mathbf{x}_i$ 为经过线性模型 $\mathbf{w}_k^T\mathbf{x}$ 后 $\mathbf{x}_i$ 为第 $k$ 个类别的置信度净输出。
  • $\mathbf{o}_i=\left[o_i^{(1)},o_i^{(2)},\cdots,o_i^{(K)}\right]$ 为样本 $\mathbf{x}_i$ 经过线性模型后的置信度净输出向量
  • $\hat{\mathbf{y}}_i=softmax(\mathbf{o}_i)=\left[softmax\left(o_i^{(1)}\right),softmax\left(o_i^{(2)}\right),\cdots,softmax\left(o_i^{(k)}\right)\right]=\left[\hat{y}_i^{(1)},\hat{y}_i^{(2)},\cdots,\hat{y}_i^{(K)}\right]$

所以目标函数为

  • 目标是预测为正确类别的置信度远远大于其他类别

通过交叉熵可以比较真实分布与预测分布的差异

  • $H(p,q)=-\sum_k p_k\log q_k\ge 0$ 为交叉熵，当 $p_k=q_k$ 时，即两个分布相同时，交叉熵有最小值0

将其作为损失函数

对参数 $\mathbf{w}_{\kappa}$ 求梯度

分类数据集

MNIST数据集 (LeCun et al., 1998) 是图像分类中广泛使用的数据集之一（手写数字识别数据集），但作为基准数据集过于简单

使用类似但更复杂的Fashion-MNIST数据集

1
2
3
4
5
6
7
8
import torch
# Pytorch对计算机视觉的实现库
import torchvision
# 对数据处理工具库
from torch.utils import data
# 视觉库中对数据操作的模块
from torchvision import transforms
from d2l import torch as d2l

下载数据集

通过torchvision内置函数将数据集下载并读取到内存

1
2
3
4
5
6
7
8
9
10
11
12
# 通过ToTensor实例将图像数据从PIL类型转换成pytorch类型，32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor()
# train=True		表示训练数据，train=False表示测试数据集
# transform=trans	表示下载后转换为tensor，不转换则只是图片
# download=True 	默认从网络下载
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", 
    train=True, 
    transform=trans, 
    download=True)
mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)

image-20240318094505252

  • 整个下载包括下载、移动、解压三步
查看数据集
1
2
3
4
5
6
7
8
9
10
# 数据集中的图片数量
len(mnist_train), len(mnist_test)
(60000, 10000)

# mnist中，每个样本用tuple表示，tuple[0]为输入，tuple[1]为其标签
# 查看第1个样本的输入张量x_1，其输出y_1为类别编号
print(mnist_train[0][0],mnist_train[0][1])
#张量类型的图片通道为1，宽高都是28，(c,h,w)=(1,28,28)
mnist_train[0][0].shape
torch.Size([1, 28, 28])
可视化数据集

批量查看图片及其标签

1
2
3
4
5
6
7
8
9
10
11
12
13
# 标签值转为标签文本
def get_fashion_mnist_labels(labels):  #@save
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    #传入的labels是一个tensor列表，for i in labels中的i为每个样本的真实标签值，
    #[text_labels]会将这些标签文本转为列表
    return [text_labels[int(i)] for i in labels]
    #相当于
    #	a = []
    #	for i in labels:
    #	    a[i]=text_labels[int(i)]
    #	return a
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#imgs为图片集，num_rows,num_cols为图片列表行列数，titles传入imgs相应的标签
def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):  #@save
    """绘制图像列表"""
    figsize = (num_cols * scale, num_rows * scale)
    _, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    return axes

读取两个样本，显示二者图像列表

1
2
X, y = next(iter(data.DataLoader(mnist_train, batch_size=2)))
show_images(X.reshape(2, 28, 28), 1, 2, titles=get_fashion_mnist_labels(y));

image-20240318101336268

实现批量读取

在每次迭代中，数据加载器每次都会[读取一小批量数据，大小为batch_size]

通过内置数据迭代器，可以随机打乱所有样本

1
2
3
4
5
6
7
8
9
10
11
12
batch_size = 256

#数据加载器可启动进程数重载
def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(
    mnist_train, 
    batch_size, 
    shuffle=True,
    num_workers=get_dataloader_workers())

可记录加载一个批量的时间

1
2
3
4
timer = d2l.Timer()
for X, y in train_iter:
    continue
f'{timer.stop():.2f} sec'

封装数据读取

从视觉库的Fashion-MNIST数据集获取训练数据集和测试数据集。

返回：训练集和验证集的数据迭代器

输入：批量大小batch_size；resize图像大小调整

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    # 对图片的处理函数列表
    #	transforms.ToTensor()：将PIL类型的图片转换为张亮
    #	transforms.Resize(resize)：调整图片大小，调整为resize
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    # 将多个图像变换操作组成一个变换操作序列
    #	输入：transforms类型的操作列表
    #	输出：返回组合后的操作序列
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(root="../data", train=False, transform=trans, download=True)
    # 返回数据集迭代器
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,num_workers=get_dataloader_workers()))

通过resize参数调整图片大小

1
2
3
4
train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break
1
torch.Size([32, 1, 64, 64]) torch.float32 torch.Size([32]) torch.int64

2.3.1 Softmax实现

获取数据集批量

1
2
3
4
5
import torch
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

初始化参数

softmax输入需要是向量，所以需要把所有图像展平，视为一个向量，$1\times 28\times 28=784$ 的列向量 $img_{[1\times28\times 28]}\rightarrow\mathbf{x}_{[784\times 1]}$

  • 展平操作会损失很多空间信息，所以卷积神经网络会弥补这一缺陷

一张图像可能得类别有10类，所以输出10维的列向量 $\mathbf{y}_{[10\times 1]}$

1
2
3
4
5
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

模型定义

输入，原始数据矩阵：每个样本展平为 $\mathbf{x}_i\in\R^{1\times d}$ 的行向量，批量样本矩阵为 $\mathbf{X}=\begin{bmatrix}\mathbf{x}_1\\\mathbf{x}_2\\\vdots\\\mathbf{x}_n\end{bmatrix}\in \mathbb{R}^{n\times d}$

  • 本例中 $\mathbf{x}_i\in\R^{1\times 784}$ ，批量数据表示为 $\mathbf{X}=\begin{bmatrix}\mathbf{x}_1\\\vdots\\\mathbf{x}_{256}\end{bmatrix}\in\R^{256\times 784}$

参数 $\mathbf{w}_k\in \mathbb{R}^{1\times d},k\in [1,K]$ ，参数矩阵 $\mathbf{W}=\begin{bmatrix}\mathbf{w}_1\\\mathbf{w}_2\\\vdots\\\mathbf{w}_{K}\end{bmatrix}\in \mathbb{R}^{K\times d}$ ，偏置 $\mathbf{b}\in \mathbb{R}^{1\times K}$ 行向量

  • 本例中，$\mathbf{w}_k\in \mathbb{R}^{1\times 784},k\in [1,10]$ ，参数矩阵 $\mathbf{W}=\begin{bmatrix}\mathbf{w}_1\\\mathbf{w}_2\\\vdots\\\mathbf{w}_{10}\end{bmatrix}\in \mathbb{R}^{10\times 784}$ ，偏置 $\mathbf{b}\in \mathbb{R}^{1\times 10}$

净输出，净输出矩阵：每个样本的净输出向量为 $\mathbf{o}_i\in \mathbb{R}^{1\times K}$ 的行向量，批量样本净输出矩阵表示为 $\mathbf{O}=\begin{bmatrix}\mathbf{o}_1\\\mathbf{o}_2\\\vdots\\\mathbf{o}_{n}\end{bmatrix}\in \mathbb{R}^{n\times K}$

  • 本例中，净输出 $\mathbf{o}_i\in \mathbb{R}^{1\times 10}$ ，批量净输出矩阵表示为 $\mathbf{O}=\begin{bmatrix}\mathbf{o}_1\\\mathbf{o}_2\\\vdots\\\mathbf{o}_{256}\end{bmatrix}\in \mathbb{R}^{256\times 10}$
1
2
3
def net(X):
    #展平操作，将256*(1,28,28)的数据展平为 256*784的张量
    return softmax(torch.matmul(X.reshape(-1,(W.shape[0])), W) + b)

所以一次softmax有三个操作

  1. 对每个项求幂 exp()
  2. 对每一行求和(在一个批量中，一行为一个样本)
  3. 将每一行除以其规范化常数，确保结果的和为1

输入：净输出矩阵

输出：softmax后的置信度矩阵 / 归一化后的置信度矩阵 $\hat{\mathbf{Y}}=\begin{bmatrix}\hat{\mathbf{y}}_1\\\hat{\mathbf{y}}_2\\\vdots\\\hat{\mathbf{y}}_{n}\end{bmatrix}=\begin{bmatrix}\hat{\mathbf{y}}_1\\\hat{\mathbf{y}}_2\\\vdots\\\hat{\mathbf{y}}_{256}\end{bmatrix}$

1
2
3
4
def softmax(O):
    O_exp = torch.exp(O)
    partition = O_exp.sum(1, keepdim=True)
    return O_exp / partition  # 这里应用了广播机制

交叉熵损失函数

对于每个样本，其交叉熵损失为

所以只需要关注真实分类对应的softmax值即可，pytorch有简便方法，根据索引列表依次从每个列表取出相应列表项，即从 $\hat{\mathbf{Y}}=\begin{bmatrix}\hat{\mathbf{y}}_1\\\hat{\mathbf{y}}_2\\\vdots\\\hat{\mathbf{y}}_{256}\end{bmatrix}$ 中，取出 $\begin{bmatrix}\hat{y}_1^{(\kappa_1)},\hat{y}_2^{(\kappa_2)},\cdots,\hat{y}_{256}^{(\kappa_{256})}\end{bmatrix}$

1
2
3
4
5
6
7
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])

y_hat[[0, 1], y]

>>> tensor([0.1000, 0.5000])
从y_hat[0]中取出y_hat[0][0],从y_hat[1]中取出y_hat[1][2]

实现交叉熵损失函数

1
2
3
4
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

# cross_entropy(y_hat, y)

精确度计算函数

1
2
3
4
5
6
7
8
9
10
11
12
13
def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    #若y_hat是矩阵，则通过argmax得出预测分类结果
    # argmax返回值最大的索引，即分类结果
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    #预测正确的样本，相应的y_hat(i)=1；预测错误，相应的y_hat(i)=0
    #	将对比结果 cmp 求和，可得预测正确的数量
    return float(cmp.type(y.dtype).sum())

#精确度
accuracy(y_hat, y) / len(y)
逐批量计算数据集的精确度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n
    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]
    def reset(self):
        self.data = [0.0] * len(self.data)
    def __getitem__(self, idx):
        return self.data[idx]

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    #若是nn框架，对模型评估，不需要更新参数，所以不计算梯度
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    #Accumulator的作用是逐批量累加
    metric = Accumulator(2)  # 正确预测数、总样本数
    with torch.no_grad():
        for X, y in data_iter:
            #在一个批量上，计算预测正确数和总样本数
            metric.add(accuracy(net(X), y), y.numel())
    #返回在当前数据集上模型的精确度       
    return metric[0] / metric[1]
1
2
3
evaluate_accuracy(net, test_iter)
#随机分类的精确度
0.1069

训练

参数迭代器

updater 是模型参数的优化函数，它接受批量大小作为参数。 它可以是d2l.sgd 函数，也可以是框架的内置优化函数

1
2
3
4
5
6
7
lr = 0.1

#作用：对参数的一次小批量随机梯度下降的更新
#输入：参数；学习率；划分的批量
#输出：更新后的参数
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)
模型的一次迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 若使用框架定义模型函数，需要计算参数的梯度，将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用自定义的优化器和损失函数
            # 	对损失函数计算梯度
            l.sum().backward()
            #使用updater中定义的梯度下降法逐批量更新参数
            updater(X.shape[0])
        #更新一轮后，将本轮的损失和、预测正确数、批量样本数累加    
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回本轮训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]
多轮迭代
1
2
3
4
5
6
7
8
9
10
11
12
def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    # 创建一个住批量显示训练指标的动态图像绘制函数
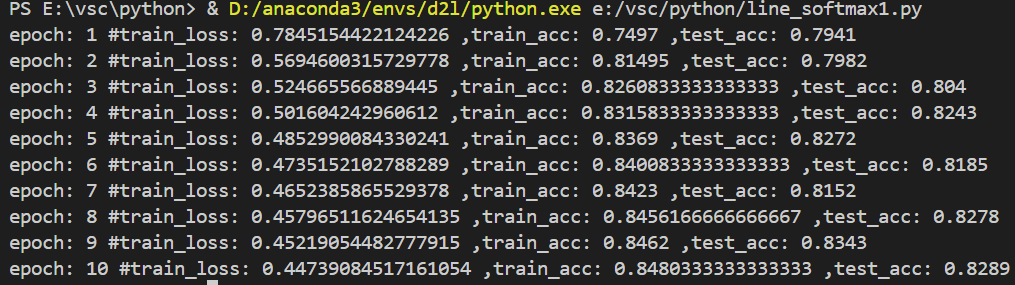
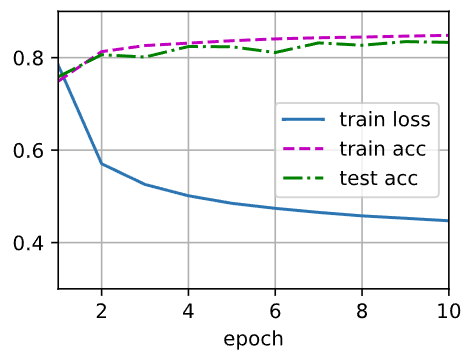
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc
1
2
num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

预测

1
2
3
4
5
6
7
8
9
10
11
def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(
        X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

整合

image-20240318212547601

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
import torch
from d2l import torch as d2l

'''1.导入数据'''
batch_size = 256

# 程序在运行时启用了多线程，而多线程的使用用到了freeze_support()函数。
# freeze_support()函数在linux和类unix系统上可直接运行，在windows系统中需要跟在main后边。
# 此处将d2l库中的get_dataloader_workers()返回值改为0，单线程运行
#输入：批量大小
#输出：训练集与测试集的可迭代对象
#作用：从torchvision库中分别下载Fashion_mnist的训练集与测试集，按批量大小划分数据集，并返回可迭代对象
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

'''2.参数初始化'''
num_inputs = 784
num_outputs = 10
W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

'''3.模型定义'''
# softmax归一化
def softmax(O):
    O_exp = torch.exp(O)
    partition = O_exp.sum(1, keepdim=True)
    return O_exp / partition  # 这里应用了广播机制
def net(X):
    #展平操作，将256*(1,28,28)的数据展平为 256*784的张量
    return softmax(torch.matmul(X.reshape(-1,(W.shape[0])), W) + b)

# X = torch.normal(0, 1, (2, 5))
# X_prob = softmax(X)
# print(X_prob, X_prob.sum(1))

'''4.交叉熵损失'''
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

##精确度
#accuracy(y_hat, y) / len(y)

'''5. 模型评估'''
#计算预测正确的样本总数
def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    #若y_hat是矩阵，则通过argmax得出预测分类结果
    # argmax返回值最大的索引，即分类结果
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    #预测正确的样本，相应的y_hat(i)=1；预测错误，相应的y_hat(i)=0
    #	将对比结果 cmp 求和，可得预测正确的数量
    return float(cmp.type(y.dtype).sum())

# y = torch.tensor([0, 2])
# y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
# y_hat[[0, 1], y]
# print(accuracy(y_hat, y) / len(y))

#定义累加器，累加器实例可以逐批量累加
class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n
    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]
    def reset(self):
        self.data = [0.0] * len(self.data)
    def __getitem__(self, idx):
        return self.data[idx]

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    #若是nn框架，对模型评估，不需要更新参数，所以不计算梯度
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    #Accumulator的作用是逐批量累加
    metric = Accumulator(2)  # 正确预测数、总样本数
    with torch.no_grad():
        for X, y in data_iter:
            #在一个批量上，计算预测正确数和总样本数
            metric.add(accuracy(net(X), y), y.numel())
    #返回在当前数据集上模型的精确度       
    return metric[0] / metric[1]

'''6. 模型训练'''
lr = 0.1
#作用：对参数的一次小批量随机梯度下降的更新
#输入：参数；学习率；划分的批量
#输出：更新后的参数
def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 若使用框架定义模型函数，需要计算参数的梯度，将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用自定义的优化器和损失函数
            # 	对损失函数计算梯度
            l.sum().backward()
            #使用updater中定义的梯度下降法逐批量更新参数
            updater(X.shape[0])
        #更新一轮后，将本轮的损失和、预测正确数、批量样本数累加    
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回本轮训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        train_loss, train_acc = train_metrics
        test_acc = evaluate_accuracy(net, test_iter)
        print("epoch:",epoch+1,"#train_loss:",train_loss,",train_acc:",train_acc,",test_acc:",test_acc)

num_epochs = 10
#输入：
#   tanin_iter对训练数据集按批量大小封装的可迭代对象
#   test_iter对测试集按批量大小封装的可迭代对象
#   loss损失函数
#   num_epochs训练次数
#   trainer参数更新器
#功能：在训练集上训练模型，使用trainer指定的参数更新方法更新模型参数，每轮训练后，在计算模型在测试集上的预测精确度，迭代指定轮数后停止
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

image-20240318204613936

image-20240318205323324

可视化预测结果

1
2
3
4
5
6
7
8
9
10
11
12
# 输入：模型；测试集；可视化测试结果
# 功能：获取1个批量的测试集，获取测试集真实标签文本，对预测结果获取预测标签文本，指定每个图片的标签格式，可视化n个结果，并显示标签
def predict_ch3(net, test_iter, n=6):  #@save
    """预测标签（定义见第3章）"""
    for X, y in test_iter:
        break
    trues = d2l.get_fashion_mnist_labels(y)
    preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
    titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
    d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])

predict_ch3(net, test_iter)

2.3.2 基于Pytorch实现Softmax

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import torch
from torch import nn
from d2l import torch as d2l
#由于d2l中没有train_ch3，所以引用手动实现中的训练主函数
import sys
sys.path.append("./")
from line_model import line_softmax1

'''1. 获取数据集'''
batch_size = 256
# 记得在windows下运行将线程数修改为1
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

'''2. 初始化模型'''
# PyTorch不会隐式地调整输入的形状。因此，在线性层前定义了展平层（flatten），来调整网络输入的形状
# softmax层输入为1*28*28=784维列向量，输出为10维列向量
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

# 输入：当前层
# 功能：若是线性层，将其权重初始化为均值为0、方差为0.01的随机值
def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

# 将初始化函数应用到网络各层，完成对线性层参数的随机初始化
net.apply(init_weights);

'''3. 损失函数定义为交叉熵'''
loss = nn.CrossEntropyLoss(reduction='none')

'''4.参数优化算法'''
# 参数：各层的参数：学习率
# 功能：获取参数优化器，利用SGD算法实现参数更新
trainer = torch.optim.SGD(net.parameters(), lr=0.1)

'''5.模型训练'''
num_epochs = 10
#输入：
#   tanin_iter对训练数据集按批量大小封装的可迭代对象
#   test_iter对测试集按批量大小封装的可迭代对象
#   loss损失函数
#   num_epochs训练次数
#   trainer参数更新器
#功能：在训练集上训练模型，使用trainer指定的参数更新方法更新模型参数，每轮训练后，在计算模型在测试集上的预测精确度，迭代指定轮数后停止
line_softmax1.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

2.3.3 关于损失函数的处理

“LogSumExp技巧”

在 softmax 前，净输出 $o_i^{(k)}$ 是一个未归一化的值，可能非常大，则 $e^{o_i^{(k)}}$ 可能会大于数据类型允许的最大数字——上溢 ，上溢会使得分母或分子无穷大，从而得到 0 、inf 、nan 的 $\hat{y}_i^{(k)}$

为避免上溢，在softmax 之前先让所有的 $o_i^{(k)}$ 减去 $\max(o^{(k)})$ ，即

在减法规范化后，可能有些 $o_i^{(k)}-\max(o_i^{(k)})$ 是比较大的负值，由于精度受限，$e^{o_i^{(k)}-\max(o_i^{(k)})}$ 会接近0——下溢 。这些值四舍五入后，使得 $\hat{\mathbf{y}}_i$ 为零，$\log(\hat{\mathbf{y}}_i)$ 会 -inf ，反向传播后会出现 nan

尽管 softmax 计算的是指数函数，但之后交叉熵损失函数是指数函数，二者结合在一起可以避免反向传播过程中的数值稳定性问题。

因此，可在交叉熵损失函数中直接使用未规范化的净输出作为损失函数

3. 前馈神经网络

3.1 多层感知机

3.1.1 线性感知机PLA

感知机解决的是二分类问题

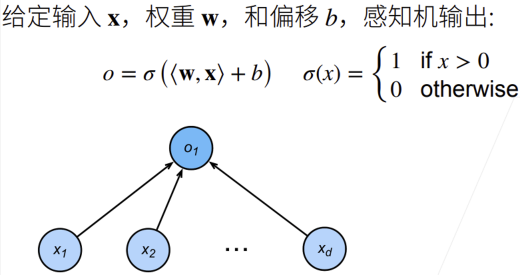
image-20240319124803900

image-20240319124830766

损失函数的梯度 $\frac{\partial \ell(y,\mathbf{x},\mathbf{w})}{\partial \mathbf{w}}=-y\mathbf{x}$ ，$\frac{\partial \ell(y,\mathbf{x},\mathbf{w})}{\partial b}=-y$

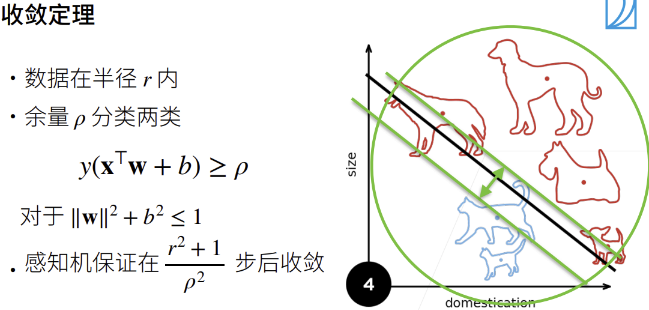
image-20240319124902919

  • 收敛步数影响因素：数据规模(越大收敛越慢)、分界余量（越大收敛越快）

缺陷：不能拟合XOR函数，因为单层感知机只能产生线性分割面

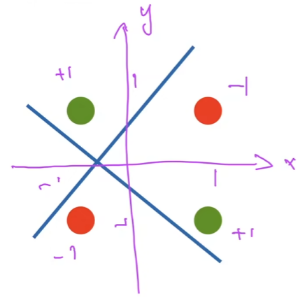
image-20240318222853913

  • $1\oplus1=1$，$-1\oplus-1=1$ ；$-1\oplus1=-1,1\oplus -1=-1$

3.1.2 多层感知机MLP

multi-layer perceptrons

XOR学习到单隐藏层感知机

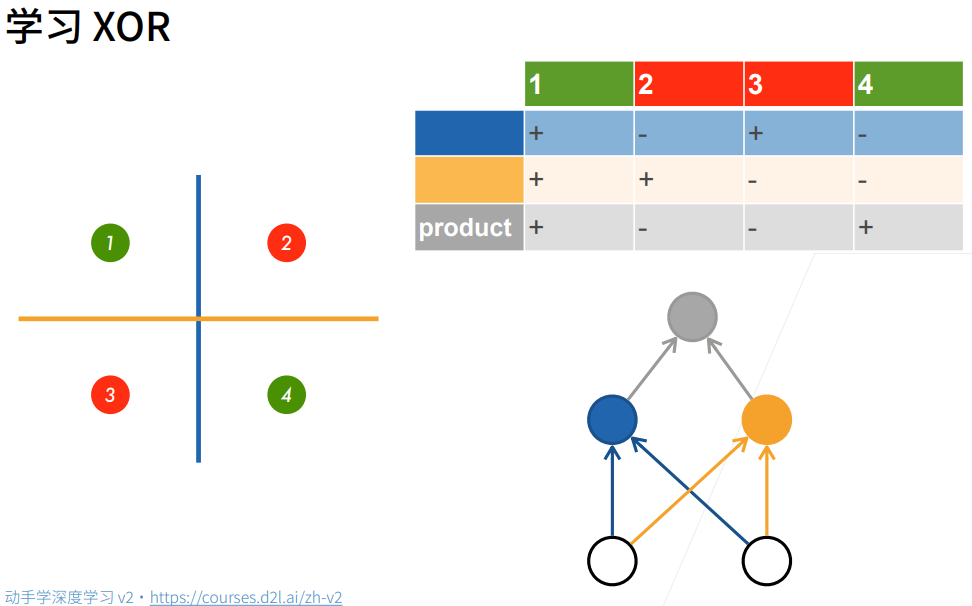
image-20240318223339988

先训练蓝色感知机，将1,3分为+类，将2,4分为-类

再训练黄色感知机，将1,2分为+类，将3,4分为-类

最后训练灰色感知机，将两个+类或两个-类分为+类，将一个+类和一个-类分为-类

单隐藏层MLP

输入 $\mathbf{x}\in \mathbb{R}^{1\times d}$

隐藏层 $\mathbf{W}_1\in \mathbb{R}^{M_1\times d}$ ，$\mathbf{b}_{1}\in \mathbb{R}^{1\times M_1}$

  • 隐藏层输出=输出层输入：$\mathbf{h}_1=\sigma(\mathbf{x}\mathbf{W}_1^T+\mathbf{b}_1)\in \mathbb{R}^{1\times M_1}$
  • $\sigma(\cdot)$ 为按元素非线性激活函数

输出层 $\mathbf{w}_2\in \mathbb{R}^{1\times M_1}$ ，$b_2\in \mathbb{R}$

  • $\hat{o}=\mathbf{h}_1\mathbf{w}_2^T+b_2\in\R$
激活函数非线性

非线性激活函数是为了避免层数塌陷

若激活函数为线性函数，经过隐藏层后输出等价于

即多层嵌套后仍然是一个线性感知器，这样的学习效果不好

激活函数类型

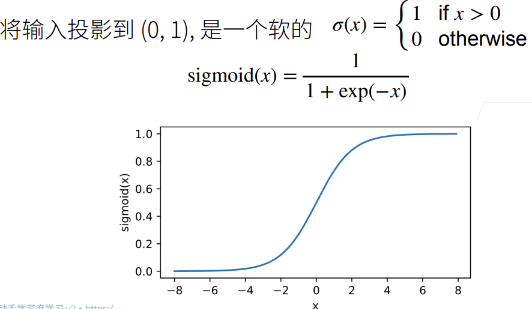
image-20240319003424239

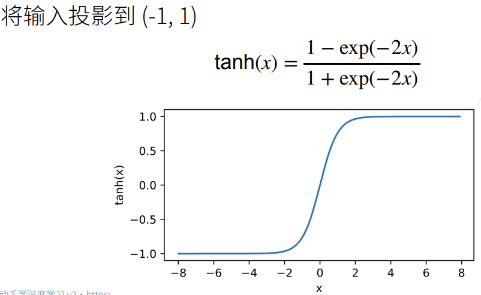
image-20240319003441350

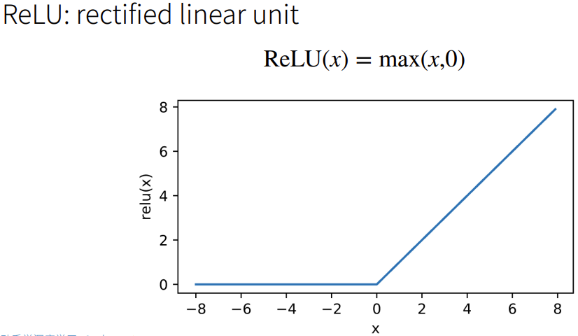
image-20240319003458955

ReLU(x)：节省资源，不需要计算指数函数

softmax与单隐藏层多分类MLP

输入 $\mathbf{x}\in \mathbb{R}^{1\times d}$

隐藏层 $\mathbf{W}_1\in \mathbb{R}^{M_1\times d}$ ，$\mathbf{b}_{1}\in \mathbb{R}^{1\times M_1}$

  • 隐藏层输出=输出层输入：$\mathbf{h}_1=\sigma(\mathbf{x}\mathbf{W}_1^T+\mathbf{b}_1)\in \mathbb{R}^{1\times M_1}$
  • $\sigma(\cdot)$ 为按元素非线性激活函数

输出层 $\mathbf{W}_2\in \mathbb{R}^{K\times M_1}$ ，$\mathbf{b}_2\in \mathbb{R}^{1\times K}$

  • $\hat{\mathbf{o}}=\mathbf{h}_1\mathbf{W}_2^T+\mathbf{b}_2\in\R^{1\times K}$
  • $\hat{\mathbf{y}}=softmax(\hat{\mathbf{o}})$

多隐藏层

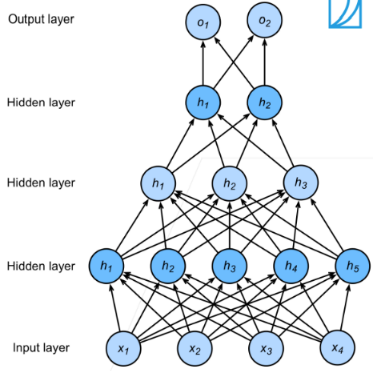
image-20240319011936498

输入 $\mathbf{x}\in \mathbb{R}^{1\times d}$

第一隐藏层 $\mathbf{W}_1\in \mathbb{R}^{M_1\times d}$ ，$\mathbf{b}_{1}\in \mathbb{R}^{1\times M_1}$

  • 第一隐藏层输出=第二隐藏层输入：$\mathbf{h}_1=\sigma(\mathbf{x}\mathbf{W}_1^T+\mathbf{b}_1)\in \mathbb{R}^{1\times M_1}$
  • $\sigma(\cdot)$ 为按元素非线性激活函数

第二隐藏层 $\mathbf{W}_2\in \mathbb{R}^{M_2\times M_1}$ ，$b_2\in \mathbb{R}^{1\times M_2}$

  • 第二隐藏层输出=第三隐藏层输入：$\mathbf{h}_2=\sigma(\mathbf{h}_1\mathbf{W}_2^T+\mathbf{b}_2)\in \mathbb{R}^{1\times M_2}$

第三隐藏层 $\mathbf{W}_3\in \mathbb{R}^{M_3\times M_2}$ ，$b_3\in \mathbb{R}^{1\times M_3}$

  • 第三隐藏层输出=输出层输入：$\mathbf{h}_3=\sigma(\mathbf{h}_2\mathbf{W}_3^T+\mathbf{b}_3)\in \mathbb{R}^{1\times M_3}$

输出层 $\mathbf{w}_4\in \mathbb{R}^{K\times M_3}$ ，$\mathbf{b}_4\in \mathbb{R}^{1\times K}$

  • $\hat{\mathbf{o}}=\mathbf{h}_3\mathbf{W}_4^T+\mathbf{b}_4\in\R^{1\times K}$
  • $\hat{\mathbf{y}}=softmax(\hat{\mathbf{o}})$
超参数设置
  • 隐藏层数
  • 每个隐藏层大小：每层隐藏层神经元个数

超参数的设置需要根据经验，越复杂的输入，参数越复杂

  • 模型越复杂，$K_1$ 越大

数据比较难：

  • 单隐藏层，$K_1$ 设置大一些
  • 网络层数深一些，相对单隐藏层的 $K_1$ ，多隐藏层的 $K_1$ 会小一些，$K_1>K_2>K_3$

数据复杂时，输入规模是比较大的，输出相对小，从输入到输出可以理解为一个压缩过程，这个压缩过程应该是逐渐变小的，这样损失的信息才最小

第一隐藏层可以选择较大的神经元，也可以对输入进行扩充，但一般不会在非第一隐藏层之后进行扩充，信息压缩后再复原是比较难得

3.1.3 MLP实现

将Fashion-mnist数据集用MLP训练

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import torch
from torch import nn
from d2l import torch as d2l

import sys
sys.path.append("./")
from line_model import line_softmax1

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

#num_inputs:输入层神经元个数
#num_outputs：输出层神经元个数
#num_hiddens：[0]-输入层神经元个数,[1]-输出层神经元个数,[2]-隐藏层神经元个数
num_inputs, num_outputs, num_hiddens = 784, 10, 256

#随机初始化，不能随机初始化为0
W1 = nn.Parameter(torch.randn(num_inputs, num_hiddens, requires_grad=True) * 0.01)
b1 = nn.Parameter(torch.zeros(num_hiddens, requires_grad=True))
W2 = nn.Parameter(torch.randn(num_hiddens, num_outputs, requires_grad=True) * 0.01)
b2 = nn.Parameter(torch.zeros(num_outputs, requires_grad=True))

params = [W1, b1, W2, b2]

def relu(X):
    a = torch.zeros_like(X)
    return torch.max(X, a)

def net(X):
    #拉成二维矩阵，一张三维图片(1,28,28)变为一维向量(1,784)；256张变为(256,784)的矩阵
    X = X.reshape((-1, num_inputs))
    H = relu(X@W1 + b1)  # 这里“@”代表矩阵乘法
    return (H@W2 + b2)

loss = nn.CrossEntropyLoss(reduction='none')

num_epochs, lr = 10, 0.1
updater = torch.optim.SGD(params, lr=lr)
line_softmax1.train_ch3(net, train_iter, test_iter, loss, num_epochs, updater)

同样训练10轮，损失降了，但精确度没降

3.1.4 基于Pytorch的MLP实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import torch
from torch import nn
from d2l import torch as d2l
import sys
sys.path.append("./")
from line_model import line_softmax1

#参数数量：
#   展平层：256*(1,28,28)->(256,784)
#   线性隐藏层(256,784)*(784, 256)->(256,256)
#   激活隐藏层
#   输出层(256,256)*(256, 10)->(256,10)
net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    # 只需要初始化线性层的参数
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)
#将参数应用到网络
net.apply(init_weights)

batch_size, lr, num_epochs = 256, 0.1, 10
# 交叉熵损失
loss = nn.CrossEntropyLoss(reduction='none')
# 对参数随机梯度下降
trainer = torch.optim.SGD(net.parameters(), lr=lr)

train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
#输入：
#   tanin_iter对训练数据集按批量大小封装的可迭代对象
#   test_iter对测试集按批量大小封装的可迭代对象
#   loss损失函数
#   num_epochs训练次数
#   trainer参数更新器
#功能：在训练集上训练模型，使用trainer指定的参数更新方法更新模型参数，每轮训练后，在计算模型在测试集上的预测精确度，迭代指定轮数后停止
line_softmax1.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

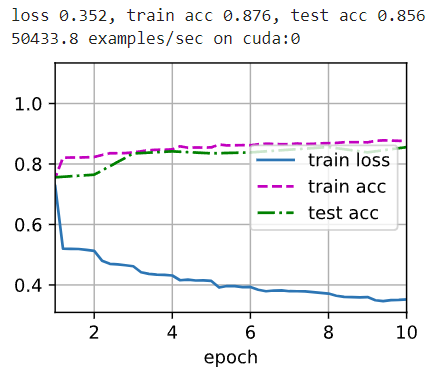
image-20240330151233579

过程中还是有一定的过拟合

3.2 全连接前馈神经网络

前馈神经网络（Feedforward Neural Network,FNN）也称为多层感知器（实际上前馈神经网络由多层softmax回归模型组成）

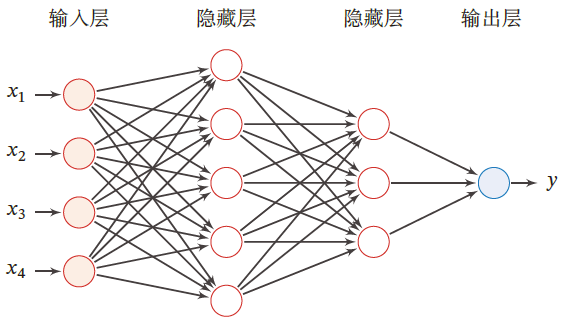
image-20231006000634803

前馈神经网络中，各个神经元属于不同的层

每层神经元接收前一层神经元的信号，并输出到下一层

  • 输入层：第0层
  • 输出层：最后一层
  • 隐藏层：其他中间层

整个网络中无反馈，信号从输入层向输出层单向传播，可用一个有向无环图表示

3.2.1 符号说明

超参数

符号含义
$L$神经网络层数
$M_l$第 $l$ 层神经元个数
$f_l(\cdot)$第 $l$ 层神经元的激活函数

参数

符号含义
$\mathbf{W}_{l}\in \mathbb{R}^{M_l\times M_{l-1}}$第 $l-1$ 层到第 $l$ 层的权重矩阵
$\mathbf{b}_{l}\in \mathbb{R}^{1\times M_l}$第 $l-1$ 层到第 $l$ 层的偏置

活性值

符号含义
$\mathbf{o}_{l}\in\R^{1\times M_l}$第 $l$ 层神经元的净输入（净活性值）
$\mathbf{h}_{l}\in \mathbb{R}^{1\times M_{l}}$第 $l$ 层神经元的输出（活性值）

3.2.2 信息传播公式

神经网络的第 $l$ 层有 $M_l$ 个神经元，相应的有 $M_l$ 个净输入和活性值，所以二者需要由 $\mathbb{R}^{1\times M_l}$ 维向量来表示

第 $l$ 层的输入为第 $l-1$ 层的活性值，相应的为 $\mathbb{R}^{1\times M_{l-1}}$ 向量

故第 $l$ 层神经元的净输入需要经过一个 仿射变换，即

获取活性值 $\mathbf{h}_{l}$ 需要经过一个 非线性变换

进而可知，由输入到网络最后的输出 $\mathbf{h}_{L}$

其中 $\mathbf{W},\mathbf{b}$ 表示网络中所有层的连接权重和偏置

前馈神经网络可以通过逐层的信息传递，整个网络可以看做一个复合函数 $\phi(\mathbf{x};\mathbf{W};\mathbf{b})$

通用近似定理

image-20240320205108341

根据通用近似定理，对于具有 线性输出层 $z^{(l)}$ 和至少一个 具有挤压性质的激活函数 $\phi(\cdot)$ 的隐藏层组成的前馈神经网络，只要隐藏层的神经元数量足够，就可以以任意精度来近似任何一个定义在实数空间中的有界闭函数

3.2.3 应用于分类任务

神经网络可以作为一个万能函数，用于进行复杂的特征转换或逼近一个条件分布

在机器学习中，输入样本的特征对分类器性能的影响很大

若要获得很好的分类效果，需要将样本的原始特征向量 $\mathbf{x}$ 转换到更有效的特征向量 $\phi(x)$ ——特征抽取

多层前馈神经网络恰好可以看做一个非线性函数 $\phi(\cdot)$ ，将输入 $\mathbf{x}\in \mathbb{R}^{1\times d}$ 映射到输出 $\phi(x)\in \mathbb{R}^{K}$ ，因此可将多层前馈神经网络看作一种特殊的特征转换方法，其输出 $\phi(x)$ 作为分类器的输入

  • $g(\cdot)$ 为分类器
  • $\theta$ 为分类器 $g(\cdot)$ 的参数
  • $\hat{\mathbf{y}}$ 为分类器输出

若分类器 $g(\cdot)$ 为 $Logistic回归$ 或 $Softmax回归$ ，则相当于在输出层引入分类器，神经网络直接输出在不同类别的条件概率 $p(\hat{\mathbf{y}}\vert \mathbf{x})$

二分类问题

对于二分类问题 $y\in \{0,1\}$ ，且采用 $Logistic回归$ ，神经网络的输出层只有一个神经元，其激活函数是 $Logistic函数$

多分类问题

对于多分类问题 $y\in \{1,\cdots,K\}$ ，如果使用 $Softmax$ 分类器，网络最后一层设置 $K$ 个神经元，其激活函数为 $Softmax$ ，网络最后一层的输出可以作为每个类的条件概率

其中，$\mathbf{o}_{L}\in \mathbb{R}^{1\times K}$ 为第 $L$ 层神经网络的净输出， $\hat{\mathbf{y}}\in\R^{1\times K}$ 为第 $L$ 层神经网络的活性值，每一维分别表示不同类别标签的预测条件概率

3.2.4 参数学习与误差反向传播

参数学习

对于一个训练样本 $(\mathbf{x},\mathbf{y})$ ，使用有 $L$ 层的神经网络，第 $l$ 层的活性值为 $\mathbf{h}_l$

其中，$\mathbf{h}_{l-1}\in \mathbb{R}^{1\times M_{l-1}}$ ，$\mathbf{W}\in\R^{M_{l}\times M_{l-1}}$ ，$\mathbf{b}_l\in \mathbb{R}^{1\times M_l}$

输出层 $\hat{\mathbf{y}}=f_L\circ f_{L-1}\cdots \circ f_1(\mathbf{x})$

若采用交叉熵损失函数，其损失函数为

给定训练集，$\mathcal{D}=\{(\mathbf{x}_i,\mathbf{y}_i)\}_{i=1}^N$ ，将每个样本 $\mathbf{x}_i$ 输入给前馈网络得到 $\hat{\mathbf{y}}_i$ ，其结构化风险函数为

  • $\lambda$ 为超参数，$\lambda$ 越大，$\mathbf{W}$ 越接近于0

  • 一般用 $Frobenius$ 范数（F范数）作为惩罚项

对于某一层网络参数，可以通过梯度下降的方法学习

可见，参数求解的核心部分为 $\frac{\partial \ell(\mathbf{y}_i,\hat{\mathbf{y}}_i)}{\partial \mathbf{W}_{l}}$ ，标量对矩阵的求导，事实上是对逐个元素求导，即

隐藏层求导

计算 $\frac{\partial \mathbf{o}_l}{\partial \mathbf{W}_l},\frac{\partial \mathbf{o}_l}{\partial \mathbf{b}_l}$ ，其中：

因 $\mathbf{o}_l=\mathbf{h}_{l-1}\mathbf{W}_l^T+\mathbf{b}_l$

  • 计算 $\frac{\partial \mathbf{o}_l}{\partial \mathbf{W}_l}\in \mathbb{R}^{M_l\times 1}$

    其中，$i\in [1,M_l],j\in [1,M_{l-1}]$

    所以有 $\frac{\partial \mathbf{o}_l}{\partial \mathbf{W}_l}\in \mathbb{R}^{M_l\times M_l\times M_{l-1}}$

  • 计算 $\frac{\partial \mathbf{o}_l}{\partial \mathbf{b}_l}$

    其中，$i\in [1,M_l]$

误差项求导

误差项 $\frac{\partial \ell(\mathbf{y}_i,\hat{\mathbf{y}}_i)}{\partial \mathbf{o}_{l}}$ 表示第 $l$ 层神经元对最终损失的影响，也反映了最终损失对第 $l$ 层神经元的敏感程度，不同神经元对网络能力的贡献程度，从而比较好地解决了贡献度分配问题

其中，

  • $\frac{\partial \mathbf{h}_l}{\partial \mathbf{o}_l}\in \mathbb{R}^{M_l\times M_l}$

  • 由于第 $l+1$ 层输入 $\mathbf{x}_{l+1}$ 为第 $l$ 层活性值 $\mathbf{h}_l$ ，$\mathbf{o}_{l+1}=\mathbf{x}_{l+1}\mathbf{W}_{l+1}^T+\mathbf{b}_{l+1}=\mathbf{h}_{l}\mathbf{W}_{l+1}^T+\mathbf{b}_{l+1}$

则有，

其中，$\odot$ 为哈达姆积，表示每个元素相乘

误差的反向传播

第 $l$ 层的误差项可以通过第 $l+1$ 层的误差项计算得到，这就是 误差的反向传播

卷积层梯度合并

所以，$\begin{bmatrix}\frac{\partial \ell}{\partial \mathbf{W}_{l}}\end{bmatrix}_{i,j}=\delta_l^{(i)}\mathbf{h}_{l-1}^{(j)}$

同理，$\ell$ 关于第 $l$ 层偏置 $\mathbf{b}_l$ 的梯度为

其中，

假设有 $L$ 层神经网络

$\mathcal{I}(\mathbf{y})$ 为 $\mathbf{y}$ 向量中元素值为1的索引

算法过程

在计算出每一层的误差项后，就可以求得本层的梯度，可以用随机梯度下降法来训练前馈神经网络

  1. 前馈计算每一层的净输入 $z^{(l)}$ 和净激活值 $a^{(l)}$ ，直至最后一层
  2. 反向传播计算每一层的误差项 $\delta^{(l)}$
  3. 计算每一层的偏导数，并更新参数

image-20231007113640918

优化问题

神经网络的参数学习比线性模型更加困难

  • 非凸优化问题
  • 梯度消失问题
非凸优化问题

神经网络的优化问题是一个非凸优化问题

image-20231007175031669

梯度消失问题
-------------本文结束-------------