AmosTian

0%

6.动手学深度学习-卷积神经网络

发表于 更新于 分类于 > >
本文字数 12.5k字 | 阅读时长 ≈ 27 分钟

[TOC]

6.0 全连接神经网络的缺陷

参数数量太多

输入规模大

图像数据的每个样本（每张图片）都由一个二维像素网格组成，取决于图片的通道数，每个像素位置有多个取值。

对于一张12M像素的图片，若是RGB，则有36M个像素数据，使用具有100个神经元的单隐藏层MLP，则其参数 $\mathbf{W}\in \mathbb{R}^{100\times 36M}$ ，参数矩阵共 3.6B 个数据需要存储。远远大于一般的待分类物品的种类数

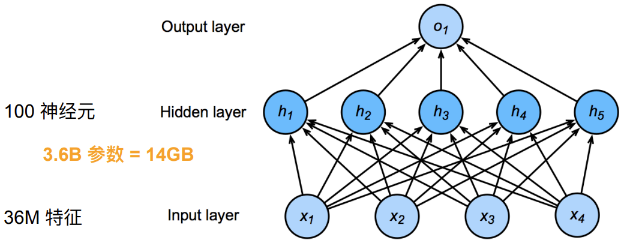
image-20240324143915388

隐藏层神经元数量

随着隐藏层的神经元数量增加，参数规模更会急剧增加

在全连接网络中，第 $l$ 层有 $M_l$ 个神经元，第 $l-1$ 层有 $M_{l-1}$ 个神经元，连接边有 $M_l\times M_{l-1}$ ，即权重矩阵 $W\in \mathbb{R}^{M_l\times M_{l-1}}$ ，当 $M_l$ 和 $M_{l-1}$ 都很大时，权重矩阵的参数会很多，训练的效率会非常低

丢失数据空间结构信息

全连接神经网络将图像展平成一维向量，再将数据送入一个全连接的多层感知机中，而忽略了每个图像的空间结构信息

自然图像中的问题有局部不变性，比如尺寸缩放、平移、旋转等操作不影响语义特征，但全连接的前馈神经网络很难提取这些局部不变的特征——数据增强

最优的结果是利用相近像素之间的相关联性学习有效的模型

平移不变性 ：不管检测对象出现在图像中的哪个位置，神经网络的前面几层都应该对相同的局部区域有相似的反应，即为平移不变性

局部性 ：神经网络的前面几层只探索输入图像中的局部区域，而不过度在意图像中相隔较远区域的关系。最后可以聚合这些局部特征，以在整个图像级别进行预测

6.1 卷积层

卷积神经网络 (convolutional neural network,CNN) 是一类强大的、为处理图像数据而设计的神经网络。基于卷积神经网络在计算机视觉领域已经占主导地位。

6.1.1 卷积层对数据空间结构信息的提取

全连接层到卷积层

输入和输出：从一维张量变为二维矩阵

权重从二维张量变为四维张量

全连接网络中，输入是一维张量，输出也为一维张量，参数矩阵为一个二维矩阵

$h_i=\sum\limits_jw_{i,j}x^{(j)}+b_i$

若使用全连接神经网络处理输入和输出都是二维张量的数据，则其参数矩阵应该是四维张量。假设相当于对一维张量的全连接神经网络等价替换，将 $h_{i}$ 替换为 $[\mathbf{H}]_{i,j}$ ，输入数据 $x^{(j)}$ 替换为 $[\mathbf{X}]_{k,l}$ ， $w_{i,j}$ 相应被替换为 $w_{i,j,k,l}$ ，所以二维输入输出的全连接神经网络为

$\mathbf{V}$ 是 $\mathbf{W}$ 的重排索引

对于隐藏层的任意净输出元素 $[\mathbf{H}]_{i,j}$ ，可以通过以 $[\mathbf{X}]_{i,j}$ 为中心对像素进行加权求和得到，权重为 $[\mathbf{V}]_{i,j,a,b}$

卷积滤波器的平移不变性

若采用上述分类器，当检测对象 $[\mathbf{X}]_{i,j}$ 在图像输入 $\mathbf{X}$ 中的位置发生平移，则仅会导致隐藏层净输出 $[\mathbf{H}]_{i,j}$ 发生平移而取值不会发生变化，即 $\mathbf{V}$ 和 $\mathbf{B}$ 并不依赖于 $(i,j)$ 的值，即 $[\mathbf{V}]_{i,j,a,b}=[\mathbf{V}]_{a,b}$ ，且 $[\mathbf{B}]_{i,j}$ 是一个常数 $b$

也就是二维卷积 / 交叉相关(数学)，使用系数 $[\mathbf{V}]_{a,b}$ 对位置 $(i,j)$ 附近的像素 $[\mathbf{X}]_{i+a,j+b}$ 进行加权得到 $[\mathbf{H}]_{i,j}$

卷积神经网络考虑到了局部特征的平移不变性，所以 $[\mathbf{V}]_{a,b}$ 的系数比全连接神经网络的系数 $[\mathbf{W}]_{i,j,a,b}$ 的数量少很多

卷积滤波器的局部性

为了收集用来训练隐净输出 $[\mathbf{H}]_{i,j}$ 的相关信息，我们不应该偏离距 $(i,j)$ 很远的地方，也就是当 $\vert a\vert,\vert b\vert>\Delta$ 时，$[\mathbf{V}]_{a,b}=0$ 。因此，可以将 $[\mathbf{H}]_{i,j}$ 重写为

image-20240324155357696

卷积层特点

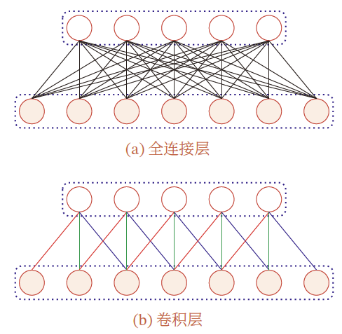
image-20240326214237577

卷积神经网络是一种深层前馈神经网络，结构特性：

  • 局部连接：与全连接的前馈神经网络相比，卷积神经网络的参数很少

  • 权重共享

  • 空间或时间上的次采样：能够高效地采样从而获得精确的模型

  • 能够高效地计算：卷积很容易用GPU并行计算

    GPU擅长进行浮点数运算

局部连接 ：在卷积层第 $l$ 层中的每个神经元只与第 $l-1$ 层在滑动窗口内的部分神经元相连，构成一个局部连接网络

  • 卷积层参数的数量大大减少，由 $M_l\times M_{l-1}$ 个连接变为 $M_l\times K$ 个连接，$K$ 为卷积核大小

权重共享：作为参数的卷积核 $\mathbf{W}_l$ 对于第 $l$ 层所有的神经元都是相同的。一个卷积核只提取输入数据中的一种特定的局部特征，若提取不同的特征，需要使用不同的卷积核

由于 局部连接 和 权重共享 的特点，一维卷积层的参数只有一个 $K$ 维的权重 $\mathbf{w}_l$ 和 1个偏置 $b_l\in \mathbb{R}$ ，即 $K+1$ 个参数

卷积滤波器的代价

卷积神经网络是包含卷积滤波器的一种特殊神经网络，$\mathbf{V}$ 被称为卷积核（convolution kernel）或滤波器或卷积层权重，权重是可以被学习的参数。

特征必须是平移不变的，并且当确定每个隐藏活性值时，每一隐藏层只包含局部的信息，只有输出层才是完整的信息。

因此卷积神经网络的权重学习依赖于归纳偏置，如图像不满足平移不变时，可能难以拟合训练数据

6.1.2 卷积运算

在信号处理和图像处理中，常用的是一维或二维卷积

一维卷积

一维卷积常用于信号处理中，用于计算信号的延迟累积

$w_i$ 称为滤波器或卷积核，假设滤波器的长度为 $K$ ，它和一个信号序列 $x_1,x_2,\cdots$ 的卷积为

  • 一般情况下，滤波器的长度 $K$ 远小于信号序列 $x$ 的长度

如：假设一个信号发生器每个时刻 $t$ 产生一个信号 $x_t$ ，其信息的衰减率为 $w_k$ ，在 $k-1$ 个时间步长后，信息变为原先的 $w_k$ 倍

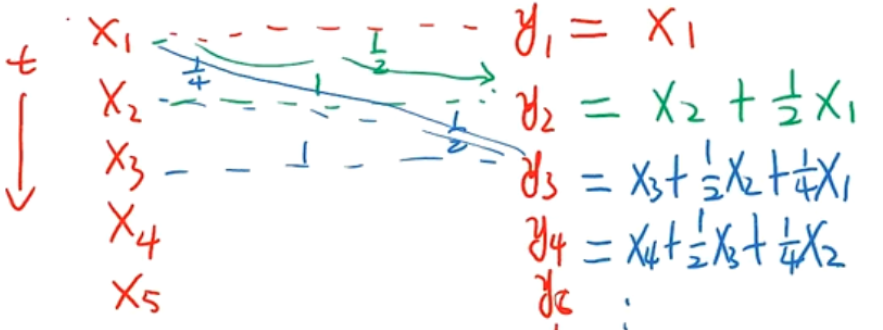
image-20231008010009731

在时刻 $t$ 收到的信号 $y_t$

二维卷积

图像是二维结构，需要将一维卷积进行扩展

给定一个图像 $\mathbf{X}\in \mathbb{R}^{n_h\times n_w}$ 和一个滤波器 $\mathbf{W}\in\R^{k_h\times k_w}$ ，一般 $k_h\ll n_h,k_w\ll n_w$ ，其卷积为

image-20231008170459092

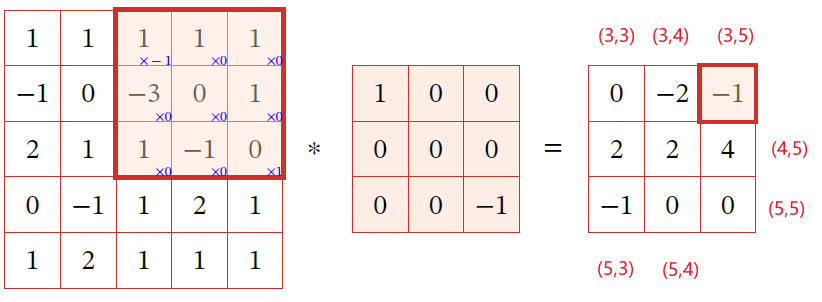
image-20231008135930046

二维卷积运算是翻转相乘

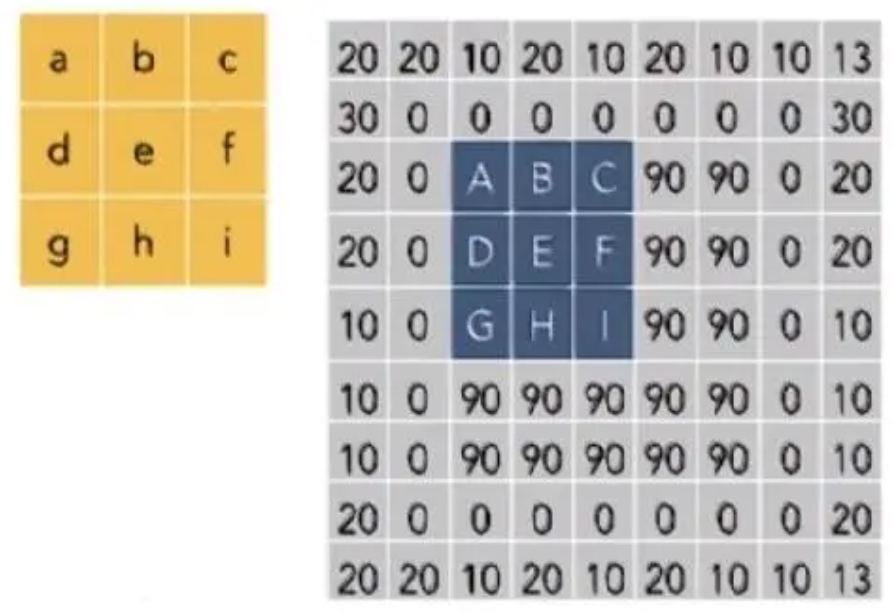
image-20231008140733004

  1. 上下翻转，左右翻转

    • 相当于在一个平面内，以 $e$ 为中心，旋转 $180^{\circ}$

  2. 再逐项相乘并求和

互相关

互相关是衡量两个序列相关性的函数，通常用滑动窗口的点积计算来实现

一个图像 $\mathbf{X}\in \mathbb{R}^{n_h\times n_w}$ 和卷积核 $\mathbf{W}\in \mathbb{R}^{k_h\times k_w}$ ，互相关为

互相关——不翻转核的卷积

  • 与卷积的区别在于卷积核是否翻转
互相关代替卷积

在计算二维卷积的过程中，需要进行卷积核翻转，卷积神经网络的实现中，一般会以互相关操作来代替卷积

两种运算的运算矩阵在数学意义上是翻转对称的(上下翻转、左右翻转)

在计算机中，用矩阵乘法实现卷积运算需要先进行翻转再相乘，后续计算与二维互相关运算相等，所以在深度神经网络中求解的是参数的值，在实际使用上并没有区别。即卷积核是否翻转与其特征提取能力无关，二维卷积与互相关在能力上是等价的

  • 通过互相关学习到的卷积核权重 $\mathbf{K}$ 与执行严格卷积运算学习到的卷积核权重 $\mathbf{K}’$ ，$\mathbf{K}’$ 翻转后就是 $\mathbf{K}$

卷积应用

一维卷积
近似微分

当令滤波器 $w=\left[\frac{1}{2},0,-\frac{1}{2}\right]$ 时，可以近似信号序列的一阶微分

  • $f’(x)=\lim\limits_{\varepsilon\rightarrow 0}\frac{f(x+\varepsilon)-f(x-\varepsilon)}{2\varepsilon}$

二阶微分，即当滤波器为 $w=[1,-2,1]$ 时，可近似实现对信号序列的二阶微分

低通滤波器/高通滤波器

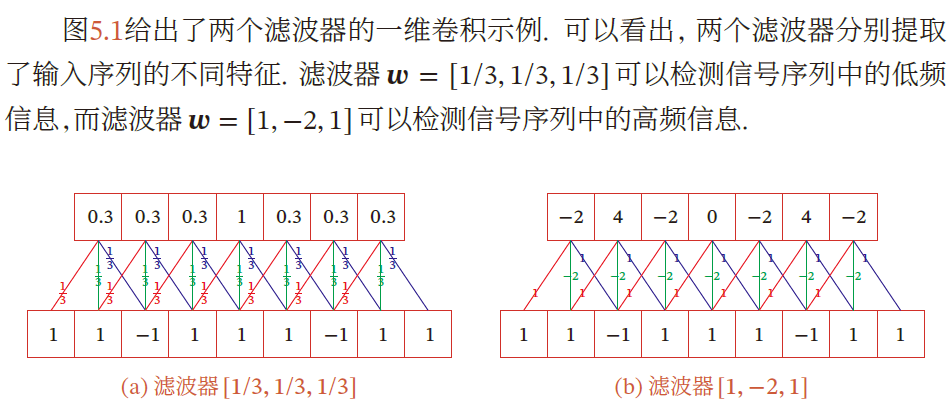
image-20231008013453175

二维卷积

常见滤波器

  • 均值滤波 将当前位置的像素值设为滤波窗口中所有像素的平均值 $w_{ab}=\frac{1}{AB}$

  • 高斯滤波器 ：用于对图像平滑去噪

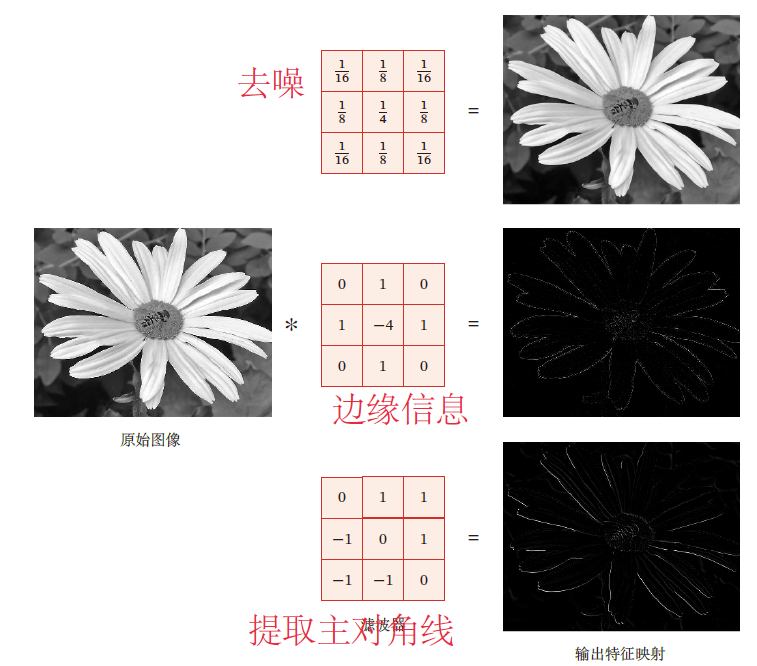
    image-20231008142002697

  • 边缘滤波器，提取边缘特征

6.1.3 卷积核大小与输出

特征映射

卷积的功能是在一个图像（或某种特征）上滑动一个卷积核（滤波器），通过卷积运算得到一组新的特征——一种局部特征提取的方法

卷积核可以被视为从输入映射到下一层的空间维度的转换器

卷积层的输出被称为 特征映射 ，每个特征映射可作为一类从原始图像中抽取的图像特征

使用不同的卷积核可以得到同一数据的不同特征映射

核大小与输出大小

在卷积层中，输入张量和核张量通过互相关产生输出张量

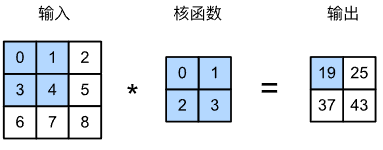
image-20240325151202612

  1. 在二维互相关运算中，卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动
  2. 当卷积核窗口滑动到输入的一个新位置，包含在该窗口内的部分张量与卷积核张量进行按元素乘，得到的张量再求和得到输出张量中的一个元素

输出大小略小于输入大小，输入高宽 $n_h\times n_w$ ，卷积核高宽 $k_h\times k_w$ ，输出大小为

6.1.4 卷积层与卷积核实现

定义互相关运算

1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
from torch import nn
from d2l import torch as d2l

def corr2d(X, K):  #@save
    """计算二维互相关运算"""
    # 卷积核的宽高一般是相等的
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i:i + h, j:j + w] * K).sum()
    return Y

验证互相关运算

1
2
3
4
5
6
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d(X, K)

#	tensor([[19., 25.],
#        [37., 43.]])

卷积层

卷积层对输入与卷积核进行互相关运算，在添加标量偏置后产生输出

在卷积层中两个被训练的参数为卷积核与偏置

1
2
3
4
5
6
7
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super().__init__()
        self.weight = nn.Parameter(torch.rand(kernel_size))
        self.bias = nn.Parameter(torch.zeros(1))
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

将带有 $h\times w$ 卷积核的卷积层称为 $h\times w$ 卷积层

应用于目标边缘检测

构造有边缘的单通道灰度图

1
2
3
4
5
6
7
8
9
X = torch.ones((6, 8))
X[:, 2:6] = 0
X
#	tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
#	        [1., 1., 0., 0., 0., 0., 1., 1.],
#	        [1., 1., 0., 0., 0., 0., 1., 1.],
#	        [1., 1., 0., 0., 0., 0., 1., 1.],
#	        [1., 1., 0., 0., 0., 0., 1., 1.],
#	        [1., 1., 0., 0., 0., 0., 1., 1.]])
  • 图像边缘为 1-0，0-1，即 X[,1] 与 X[,6]

构造 $1\times 2$ 卷积核进行互相关运算，若水平相邻的两元素相同，则输出为零；对于图像边界，输出为1

1
K = torch.tensor([[1.0, -1.0]])

执行互相关运算

1
2
3
4
5
6
7
8
Y = corr2d(X, K)
Y
#	tensor([[ 0.,  1.,  0.,  0.,  0., -1.,  0.],
#	        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
#	        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
#	        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
#	        [ 0.,  1.,  0.,  0.,  0., -1.,  0.],
#	        [ 0.,  1.,  0.,  0.,  0., -1.,  0.]])
  • $Y$ 中1表示白色到黑色边缘，-1表示黑色到白色边缘

这个卷积层只能检测垂直边缘，无法检测水平边缘

参数学习

通过 输入-输出 学习由 $X$ 生成 $Y$ 的卷积核

  1. 将卷积核初始化
  2. 每轮迭代，比较 $Y$ 与卷积输出 $\hat{Y}$ 的平方误差，通过梯度更新卷积核
1
2
3
4
5
6
7
# 构造一个二维卷积层，它具有1个输出通道和形状为（1，2）的卷积核
conv2d = nn.Conv2d(1,1, kernel_size=(1, 2), bias=False)

# 这个二维卷积层使用四维输入和输出格式（批量大小、通道、高度、宽度），
# 其中批量大小和通道数都为1
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
1
2
3
4
5
6
7
8
9
10
11
lr = 3e-2  # 学习率

for i in range(10):
    Y_hat = conv2d(X)
    l = (Y_hat - Y) ** 2
    conv2d.zero_grad()
    l.sum().backward()
    # 迭代卷积核
    conv2d.weight.data[:] -= lr * conv2d.weight.grad
    if (i + 1) % 2 == 0:
        print(f'epoch {i+1}, loss {l.sum():.3f}')

在10轮迭代后，误差已经降到足够低，学习到的卷积核权重张量

1
2
conv2d.weight.data.reshape((1, 2))
#	tensor([[ 1.0010, -0.9739]])

6.1.5 卷积核与感受野机制

感受野机制：听觉、视觉等神经系统中的一些神经元，只接受其所支配的刺激区域内的信号

  • 一个视觉皮层的神经元的感受野指视网膜上的特定区域，只有这个区域内的刺激才能激活该神经元

在神经网络中，对于某一层的任意元素 $x$ ，其 感受野 指在前向传播过程中可能影响 $x$ 取值的所有元素（来自所有先前层）

感受野可能大于输入的实际大小

image-20240325151202612

19的感受野是输入阴影部分的四个元素，假设输出 $\mathbf{Y}$ ，其后再添加一个卷积层，输出单个元素 $z$ ，$z$ 的感受野除 $\mathbf{Y}$ 上的四个元素之外，还有输入 $\mathbf{X}$ 上的9个元素

因此，当特征图中的任意元素需要检测更广区域的局部特征时，可以构建更深的网络

6.2 卷积层超参数

卷积输出的形状取决于输入形状与卷积核形状，同时也取决于超参数的设置，步长和填充是控制卷积层输出大小的两个超参数

为什么需要填充：在连续应用多次卷积后，我们最终得到的输出远小于输入大小——卷积核通常大于1

  • 一个 $240\times 240$ 像素的图像，经过10层 $5\times 5$ 的卷积后，将减少到 $200\times 200$ 像素

这样，原始图像的边界丢失了很多有用信息，填充是解决此问题的有效方法

而对于原始的输入分辨率十分冗余的情况下，增大步幅可以快速降低图像的宽度和高度

填充（慢缩放）：在 输入 的边界进行零填充，使卷积层输出变大

  • 输入规模小，又想用深的网络

  • 输入数据对称，则会使用对称填充

步幅（快缩放）：使卷积层输出变小

  • 输入规模大，使输入规模成倍减少，减少计算量

6.2.1 一维卷积上的填充与步幅

在卷积的标准定义基础上，还可以引入卷积核的 滑动步长 (stride) 和 零填充(zero padding) 来增加卷积的多样性

步长S：卷积核在滑动时，滑动窗口的间隔；滑动窗口在一个时间间隔后滑动S个数据

  • 增加步长，减少输出长度

零填充：在输入向量的两端补零

  • 增加填充，增加输出长度

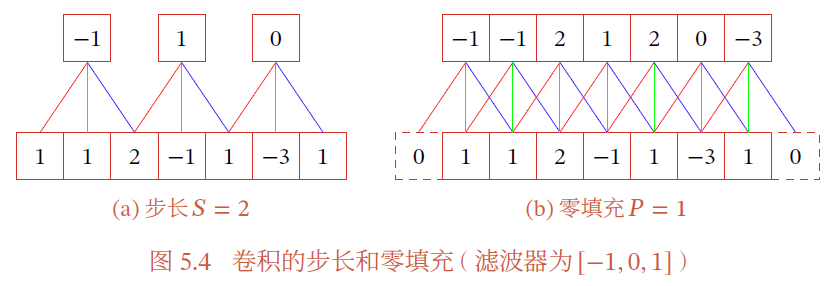
image-20231008103256666

假设卷积层的输入神经元个数为 $N$ ，卷积大小为 $K$ ，步长为 $S$ ，在输入两端分别补 $\frac{P}{2}$ 个零，那么该卷积的神经元数量为 $\frac{N-K+P}{S}+1$

  • 窄卷积：$S=1$ ，$P=0$ ，卷积后输出长度为 $N-K+1$
  • 等宽卷积：$S=1$ ，$P=K-1$ ，卷积后输出长度为 $N$
  • 宽卷积：$S=1$，$P=2K-2$，卷积后输出长度为 $N+K-1$

6.2.2 二维卷积上的填充与步幅

填充

在输入图像的边界填充元素，若进行 $p_h$ 行填充和 $p_w$ 列填充，相当于输入的行列分别增加 $p_w$ 和 $p_h$

  • 通常在行列上平均 $p_h$ 和 $p_w$ 个填充，即 $\frac{p_h}{2}$ 在顶部，$\frac{p_h}{2}$ 个填充在底部

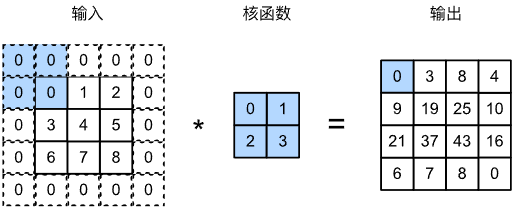
image-20240325165637559

则输出形状变为

通常，我们希望一次卷积后，不损失信息，即输入输出形状相等。因此，将填充设置为 $p_h=k_h-1,p_w=k_w-1$ 可使输入和输出形状相同

卷积核的高和宽通常为奇数，选择奇数的好处是上下和左右填充数相等

  • 若 $k_h$ 是奇数，则在上下填充 $\frac{p_h}{2}$ 行
  • 若 $k_h$ 为偶数，一种情况是上添加 $\lceil \frac{p_h}{2}\rceil$ 行，下添加 $\lfloor \frac{p_h}{2}\rfloor$

若输入和输出具有相同高度，卷积核的大小是奇数且上下、左右填充数相等，则 Y[i,j] 可以视为以输入 X[i,j] 为中心与卷积核进行互相关运算得到的

实现

创建 $3\times 3$ 的二维卷积核，进行 $p_h=p_w=2$ 的零填充，输入的高宽为 $8\times 8$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
from torch import nn

# 此函数初始化卷积层权重，并对输入和输出提高和缩减相应的维数
def comp_conv2d(conv2d, X):
    # (1,1)+X.shape为拼接运算，将 (1,1)+(8,8)=(1,1,8,8) 以使用nn框架提供的卷积运算
    # 	(1,1,8,8)表示批量大小和通道数都是1
    X = X.reshape((1, 1) + X.shape)
    Y = conv2d(X)
    # 省略前两个维度：批量大小和通道
    return Y.reshape(Y.shape[2:])

# 请注意，这里每边都填充了1行或1列，因此总共添加了2行或2列
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1)
X = torch.rand(size=(8, 8))
comp_conv2d(conv2d, X).shape
#	torch.Size([8, 8])

同样，由于输入的宽高不同，所以也会使用高度和宽度不同的卷积核，这是可以 高度和宽度 分别进行不同数量的填充

1
2
3
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1))
comp_conv2d(conv2d, X).shape
#	torch.Size([8, 8])

步幅

在计算互相关时，卷积核窗口从输入张量的左上角开始，向下、向右滑动。每次默认滑动一个窗口，可以通过设置 步幅 (stride)超参数，每次滑动多个元素

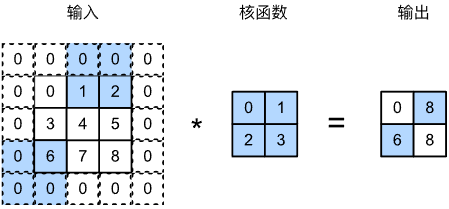
image-20240325173304985

如图所示，计算 $[\mathbf{Y}]_{1,2}$ 后再计算 $[\mathbf{Y}]_{2,1}$ 时，滑动窗口向下滑动3个元素，向左滑动2个元素，即图中进行的运算是

  1. 对输入进行 $p_h=p_2=2$ 的零填充
  2. 垂直步幅为3，水平步幅为2的二维互相关运算

若设置垂直填充与水平填充为 $p_h,p_w$ ，垂直步幅与水平步幅为 $s_h,s_w$ 时，输出形状为

若填充为 $p_h=k_h-1$ ，$p_w=k_w-1$ ，则输出形状为 $\bigg\lfloor \frac{n_h+s_h-1}{s_h}\bigg\rfloor\times \bigg\lfloor\frac{n_w+s_w-1}{s_w}\bigg\rfloor$ 。此时，若输入高度和宽度可以被垂直和水平步幅整除，则输出形状为 $\frac{n_h}{s_h}\times\frac{n_w}{s_w}$

1
2
3
4
# 填充为2=卷积核-1；且输入可被步长整除
conv2d = nn.Conv2d(1, 1, kernel_size=3, padding=1, stride=2)
comp_conv2d(conv2d, X).shape
#	torch.Size([4, 4])

简写

为简洁表达，当输入高度和宽度两侧的填充数量分别是 $p_h$ 和 $p_w$ 时，我们称之为填充 $(p_h,p_w)$ 。当 $p_h=p_w=p$ 时，我们称填充为 $p$

当垂直步幅和水平步幅分别为 $s_h$ 和 $s_w$ 时，我们称之为步幅 $(s_h,s_w)$ 。当 $s_h=s_w=s$ 时，称步幅为 $s$

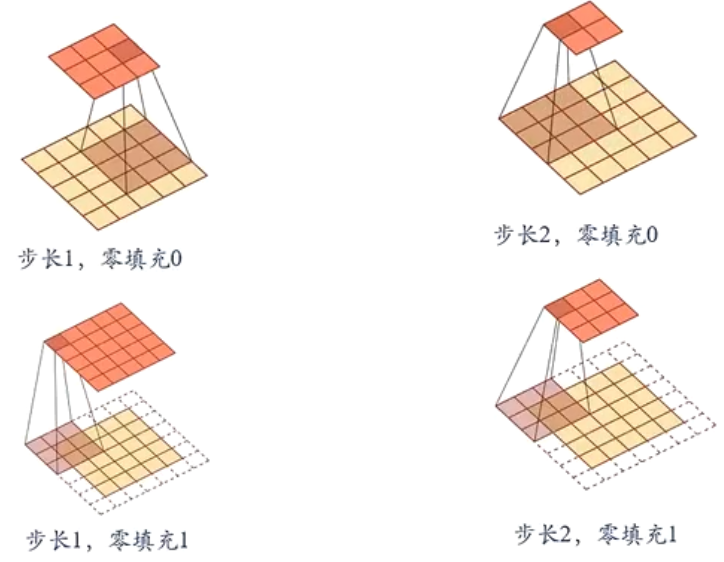
image-20231008170616755

  • 窄卷积：$p_h=p_w=0$ ，$s_h=s_w=1$ ，卷积后输出形状为 $(n_h-k_h+1)\times (n_w-k_w+1)$
  • 等宽卷积：$s_h=s_w=1$ ，$p_h=k_h-1,p_w=k_w-1$ ，卷积后输出长度为 $n_h\times n_w$
  • 宽卷积：$s_h=s_w=1$，$p_h=2(k_h-1),p_w=2(h_w-1)$，卷积后输出长度为 $(n_h+k_h-1)\times (n_w+k_w-1)$

卷积与互相关运算的交换性

  • 数学上，$*$ 表示卷积运算，$\otimes$ 表示互相关与运算
  • 但在 torch 中，$$ 表示矩阵乘时，运算结果与互相关运算结果一致，所以此处用 $$ 表示互相关运算，$\otimes$ 表示卷积

交换性：$x\otimes y=y\otimes x$

二维图的宽卷积具有交换性

  • 二维宽卷积：二维图像 $X\in \mathbb{R}^{n_h\times n_w}$ 和 二维卷积核 $W\in \mathbb{R}^{k_h\times k_w}$ ，对 $X$ 进行零填充，两端各补 $k_h-1$ 个零和 $k_w-1$ 个零，得到全填充的图像 $\tilde{X}\in \mathbb{R}^{(n_h+2k_h-2)\times (n_w+2k_w-2)}$

图像 $X$ 和卷积核 $W$ 的宽卷积定义为

当输入信息和卷积核有固定长度时，他们的宽卷积具有交换性，

由于卷积与互相关运算的区别只有是否翻转卷积核，相应的宽互相关也有交换性

6.2.3 通道

多输入通道

图像实质上一般包含三个通道 / RGB ，即一张图片是 $颜色\times 高度\times 宽度$ 组成的三维张量

  • 直观上，可以将一个三维张量想象为一系列二维张量堆叠成的通道。

    后两个维度表示像素的空间位置，第一个维度看作每个像素的多维表示

    图 2

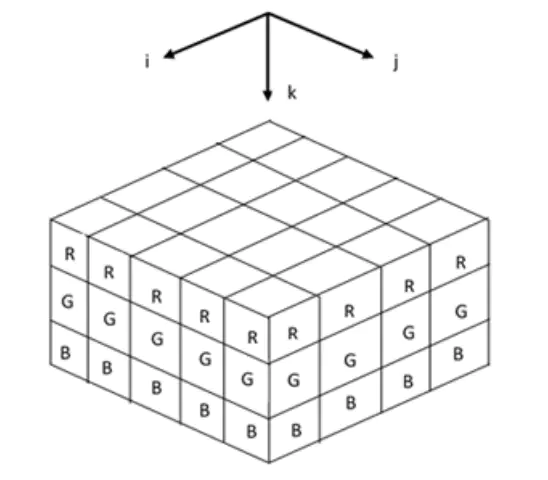
    一个通道为后续层提供一种空间化的学习特征

所以实际上一张图片表示为 $[\mathbf{X}]_{c_i,n_h,n_w}$ ，卷积核也应该相应调整为 $[\mathbf{V}]_{c_i,a,b}$

由于输入和卷积核都有 $c_i$ 个通道

  1. 对每个通道输入的二维张量 $\mathbf{X}_{n_h\times n_w}$ 与该通道的卷积核 $K_{k_h\times k_w}$ 进行互相关运算，并加偏置 $[\mathbf{b}]_d\in \mathbb{R}$
  2. 对 $c_i$ 个通道互相关运算的结果求和，得到一个二维张量 $\mathbf{H}_{(n_h-k_h+1)\times(n_w-k_w+1)}$

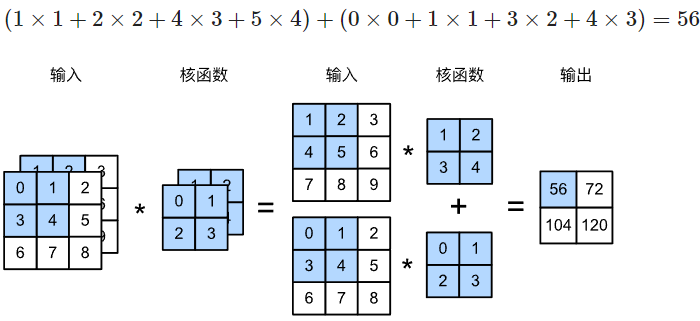
image-20240325214225193

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import torch
from d2l import torch as d2l

def corr2d_multi_in(X, K):
    # 先遍历“X”和“K”的第0个维度（通道维度），再把它们加在一起
    return sum(d2l.corr2d(x, k) for x, k in zip(X, K))
	# zip(X,K)将序列X和K打包为元组的列表，每个元组包含X和K的一个元素
    #	X是[1, 2, 3],K是['A','B','C']:
    #		zip(X, K)=[(1,'A'),(2,'B'),(3,'C')]

X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
               [[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])

corr2d_multi_in(X, K)
# tensor([[ 56.,  72.],
#         [104., 120.]])

多输出通道

实际上，我们会同时获取同一张图片的不同空间化特征，如：在靠近输入的底层，一些通道专门识别边缘、一些通道识别纹理特征。即输入是多通道的 $c_i\times n_h\times n_w$ ，卷积层输出也是多通道的 $c_o\times m_h\times m_w$ ， 因此，每个空间化特征应该设计各自的卷积核，即 $c_o$ 个 $c_i\times k_h\times k_w$ 的卷积核

  • 每层的通道都会为后续层提供一组空间化的学习特征

    image-20240325223750954

为了支持输入 $\mathbf{X}$ 和隐藏层 $\mathbf{H}$ 中的多个通道，卷积核需要再增加一维表示不同通道

其中，

1
2
3
4
def corr2d_multi_in_out(X, K):
    # 迭代“K”的第0个维度，每次都对输入“X”执行互相关运算。
    # 最后将所有结果都叠加在一起
    return torch.stack([corr2d_multi_in(X, k) for k in K], 0)

简单的将核张量 K、K+1、K+2 作为第零、第一、第二输出通道的卷积核

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
K = torch.stack((K, K + 1, K + 2), 0)
K.shape
#	torch.Size([3, 2, 2, 2])

对输入张量X与卷积核张量K执行互相关运算，输出含3个通道
第1个通道输出结果与单输出通道输出结果一致
corr2d_multi_in_out(X, K)
#	tensor([[[ 56.,  72.],
#	         [104., 120.]],
#	
#	        [[ 76., 100.],
#	         [148., 172.]],
#	
#	        [[ 96., 128.],
#	         [192., 224.]]])

  • torch.stack(inputs, dim=?) ，假设 len(inputs)=l ，且输入元组的每个元素形状都是 $m\times n$ ，则

  • 对于

    1
    2
    >>> T1 = torch.tensor([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
    >>> T2 = torch.tensor([[10, 20, 30], [40, 50, 60], [70, 80, 90]])

    image-20240325234035776

    • dim=0 则输出形状为 $l\times m\times n$

      1
      2
      3
      4
      5
      6
      7
      8
      torch.stack((T1,T2),dim=0)
      tensor([[[ 1,  2,  3],
               [ 4,  5,  6],
               [ 7,  8,  9]],

              [[10, 20, 30],
               [40, 50, 60],
               [70, 80, 90]]])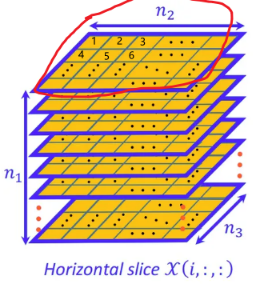

      image-20240326002359645

    • dim=1 则输出形状为 $m\times l\times n$

      1
      2
      3
      4
      5
      6
      7
      8
      9
      >>> torch.stack((T1,T2),dim=1)
      tensor([[[ 1,  2,  3],
               [10, 20, 30]],

              [[ 4,  5,  6],
               [40, 50, 60]],

              [[ 7,  8,  9],
               [70, 80, 90]]])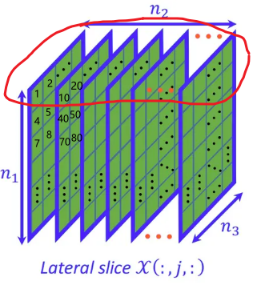

      image-20240326002744100

    • dim=2 则输出形状为 $m\times n\times l$

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      >>> torch.stack((T1,T2),dim=2)
      tensor([[[ 1, 10],
               [ 2, 20],
               [ 3, 30]],

              [[ 4, 40],
               [ 5, 50],
               [ 6, 60]],

              [[ 7, 70],
               [ 8, 80],
               [ 9, 90]]])

      image-20240326003045452

    dim 指定了新维度的位置

总结

卷积核：高度和宽度维度上识别相邻元素间相互作用

输出通道：每个输出通道输出各自通道可以识别的特定局部特征

输入通道：对局部特征的组合——相加

越底层，识别的特征越局部；随着网络层数的加深，组合的特征数越来越多，越接近真实结果

  • 从感受野机制理解，越底层，感受野越小，识别的局部特征越小；越顶层，其感受野越大，识别并组合的局部特征越多，越接近真实的输出

1维卷积

$k_h=k_w=1$ 的卷积核，可以实现同一元素位置上信息的跨通道组合

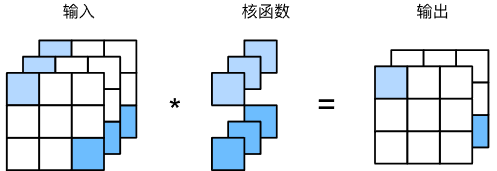
image-20240326004043596

1维卷积应用在每个像素位置的不同通道相当于输入形状为 $n_hn_w\times c_i$ 权重为 $c_o\times c_i$ 的全连接层

以 $c_i$ 个输入值转换为 $c_o$ 个输出值，所以 $1\times 1$ 卷积层需要权重维度为 $c_o\times c_i$

1
2
3
4
5
6
7
8
9
10
11
12
13
def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.reshape((c_i, h * w))
    K = K.reshape((c_o, c_i))
    # 全连接层中的矩阵乘法
    Y = torch.matmul(K, X)
    return Y.reshape((c_o, h, w))

X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))

Y1 = corr2d_multi_in_out_1x1(X, K)
$1\times 1$ 卷积核的作用

  1. 降维/升维

    img

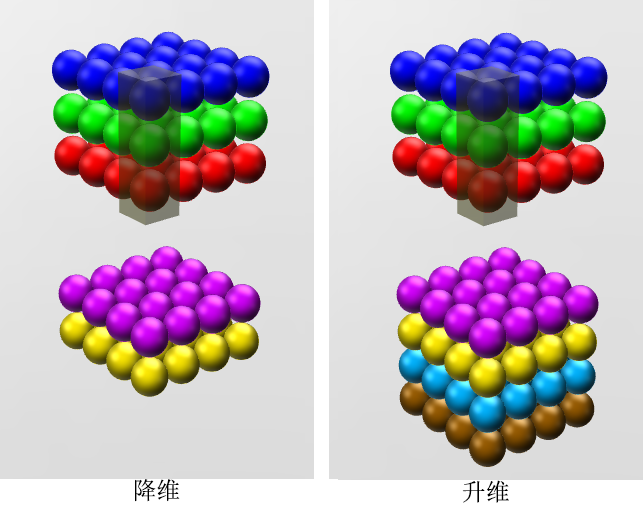
    $1\times 1$ 的卷积核不会改变宽度和长度，直观看可以改变深度，即通道数

    降维：可以通过减少通道数来减少参数，进而可以进行数据的降维处理

    • 假设有一个 $M\times N\times 3$ 的图像，通过 $1\times 1\times 3\times 2$ ($D=3,P=2$ ) 的卷积核处理，得到 $M\times N\times 2$ 的特征映射，达到降维目的

    升维：同样可以通过增加通道数来增加参数，对数据进升维处理

    • 同样的输入，经过 $1\times 1\times 3\times 4$ 的卷积核处理，得到 $M\times N\times 4$ 的特征映射，达到升维的目的

  2. 跨通道信息整合

    使用 $1\times 1$ 的卷积核，实现降维和升维的操作其实是利用通道间信息的线性组合，

    $3\times 3\times 64$ 的输入，经过 $1\times 1\times 64\times 28$ 的卷积核，就变成了 $3\times 3\times 28$ 的输出，可以理解为原来的64个通道的输入跨通道线性组合变成了28个通道，这就是通道间的信息交互

  3. 减少计算量

    img

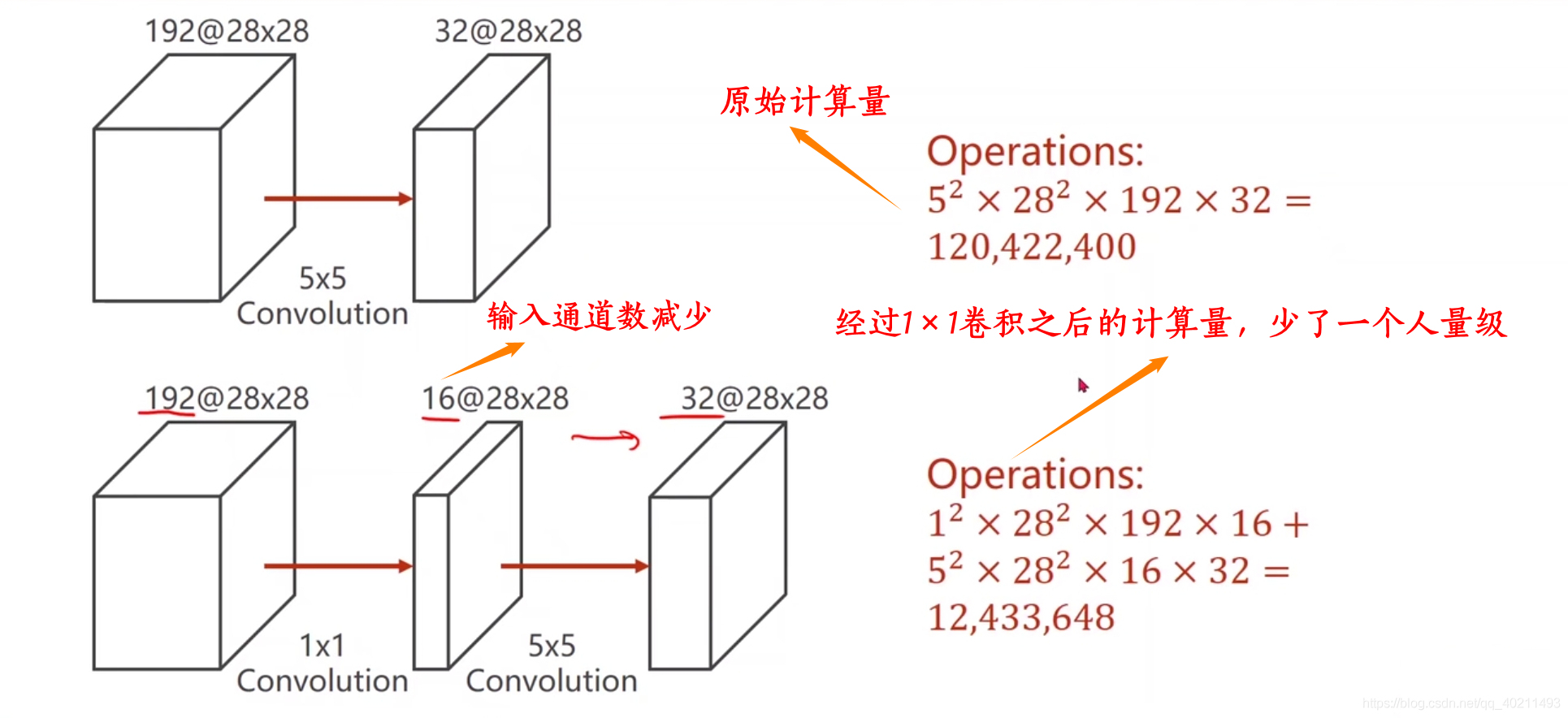
    原先：

    $Z^{(l,p)}=\sum\limits_{d=1}^DW^{(l,p,d)}\otimes X^{(l-1,d)}+b^{(l,p)}$ ，对于一次卷积，需要经过 $M’\times N’\times U\times V$ 次乘法，故若要计算上述输入特征映射，需要 $P\times D\times M’\times N’\times U\times V=32\times 192\times 5^2\times 28^2$

  4. 增加网络的深度，添加非线性，增强神经网络的表达能力

    增加网络深度好处：卷积核越大，网络的深度也就增加。随着网络深度的增加，越靠后的特征图上的节点感受野也越大。因此特征也越来越形象，也就是更能看清这个特征是个什么东西。层数越浅，就越不知道这个提取的特征到底是个什么东西。

    添加非线性：想在不增加卷积核大小的情况下，让网络加深，可以加一层 $1\times 1$ 的卷积核，在不改变输入规模的情况下，一个卷积层包含激活和池化，相当于多了一个非线性的激活函数，如 $ReLU$ 和 $Sigmod$

    卷积层之后经过激励层，经过卷积核得到的特征映射，可以添加非线性激活函数，提高网络的表达能力

6.2.4 二维卷积层一般形式

二维卷积层的一般形式

时间复杂度

对于每个输出 $[\mathbf{H}]_{i,j}$ ，需要在 $c_i$ 个通道上分别进行 $k_h\times k_w$ 次乘法，每个输出通道有 $m_h\times m_w$ 个元素，共有 $c_o$ 个通道，所以计算时间复杂度为 $O(c_o\times c_i\times k_h\times k_w\times m_h\times m_w)$ 次浮点数运算

如：$c_i=c_o=100$ ，$k_h=k_w=5$，$m_h=m_w=64$ ，则需要进行 $1024\times 10^6=1GFLOP$

若有10层卷积层，样本数量为1M，前向运算则需要 $10P$ 次浮点数运算

CPU每秒大约0.15T次浮点数运算，大约需要18h

GPU每秒大约12T次浮点数运算，大约需要14min

6.3 卷积神经网络

CNN结构：卷积层；汇聚层；

6.3.1 结构

卷积层

输入：$\mathbf{X}\in \mathbb{R}^{c_i\times n_h\times n_w}$ ，每个输入通道的数据 $[\mathbf{X}]_{d}$ 为一个输入分量，$d\in [1,c_i]$

输出：$\mathbf{Y}\in \mathbb{R}^{c_o\times m_h\times m_w}$ ，每个输出通道的数据 $[\mathbf{Y}]_{p}$ 为一个输出分量，$p\in [1,c_o]$

卷积核：$\mathbf{W}\in \mathbb{R}^{c_o\times c_i\times k_h\times k_w}$ ，对于一个输出通道上的输出 $[\mathbf{Y}]_{p}$ ，各输入通道都对应一个 $k_h\times k_w$ 的卷积核 $[\mathbf{W}]_{p,d}$

  • 每个卷积核都对应一个实数偏置，即 $[\mathbf{B}]_{p,d}\in \mathbb{R}$

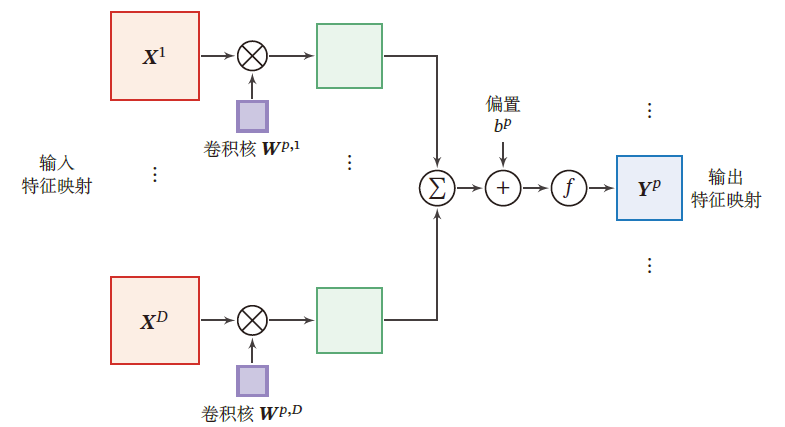
image-20231009111129159

即输出层的一个特征映射为

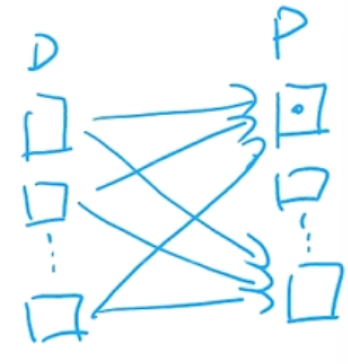
image-20231009111106366

所以 输入通道和输出通道间的特征映射是全连接的

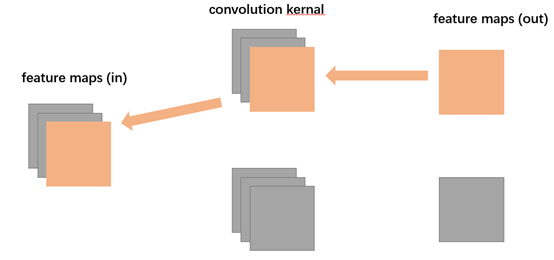
卷积核

卷积核 $\mathbf{W}\in\R^{c_o\times c_i\times k_h\times k_w}$ 为四维张量，其中每个切片矩阵 $[\mathbf{W}]_{p,d}$ 为一个二维卷积核，$p\in [1,c_o],d\in [1,c_i]$

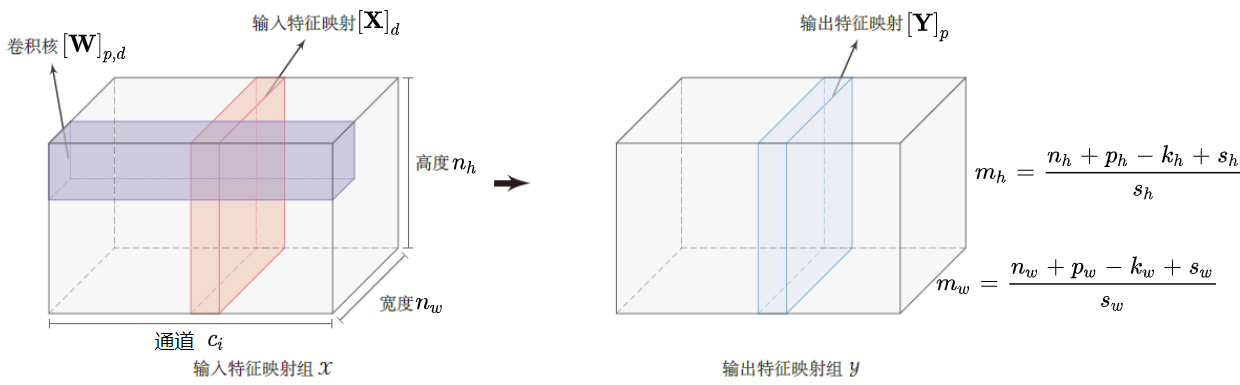
image-20240327103321437

一个输出通道上的值 $[\mathbf{Y}]_p$ 需要该输出通道对应的 $c_i$ 个输入通道上的卷积核 $[\mathbf{W}]_{p,d}$ 与输入通道的 $c_i$ 个分量分别卷积

  • 图上画的是一次卷积过程，实际上要得到蓝色的输出矩阵需要 $c_i$ 次卷积运算，所以输入特征应该是 $c_i$ 个粉矩阵才对，图有点问题

  • 展开是这么个过程，2个输出通道，3个输入通道 $[\mathbf{X}]_{d}\in \mathbb{R}^{5\times 5}$ ，所以有 $c_o\times c_i=2\times 3=6$ 个卷积核 $[\mathbf{W}]_{p,d}\in R^{3\times 3}$，填充 $p=2$ ，步长 $s=2$ ，即经过卷积，输出大小为 $\frac{5+2+2-3}{2}=3$

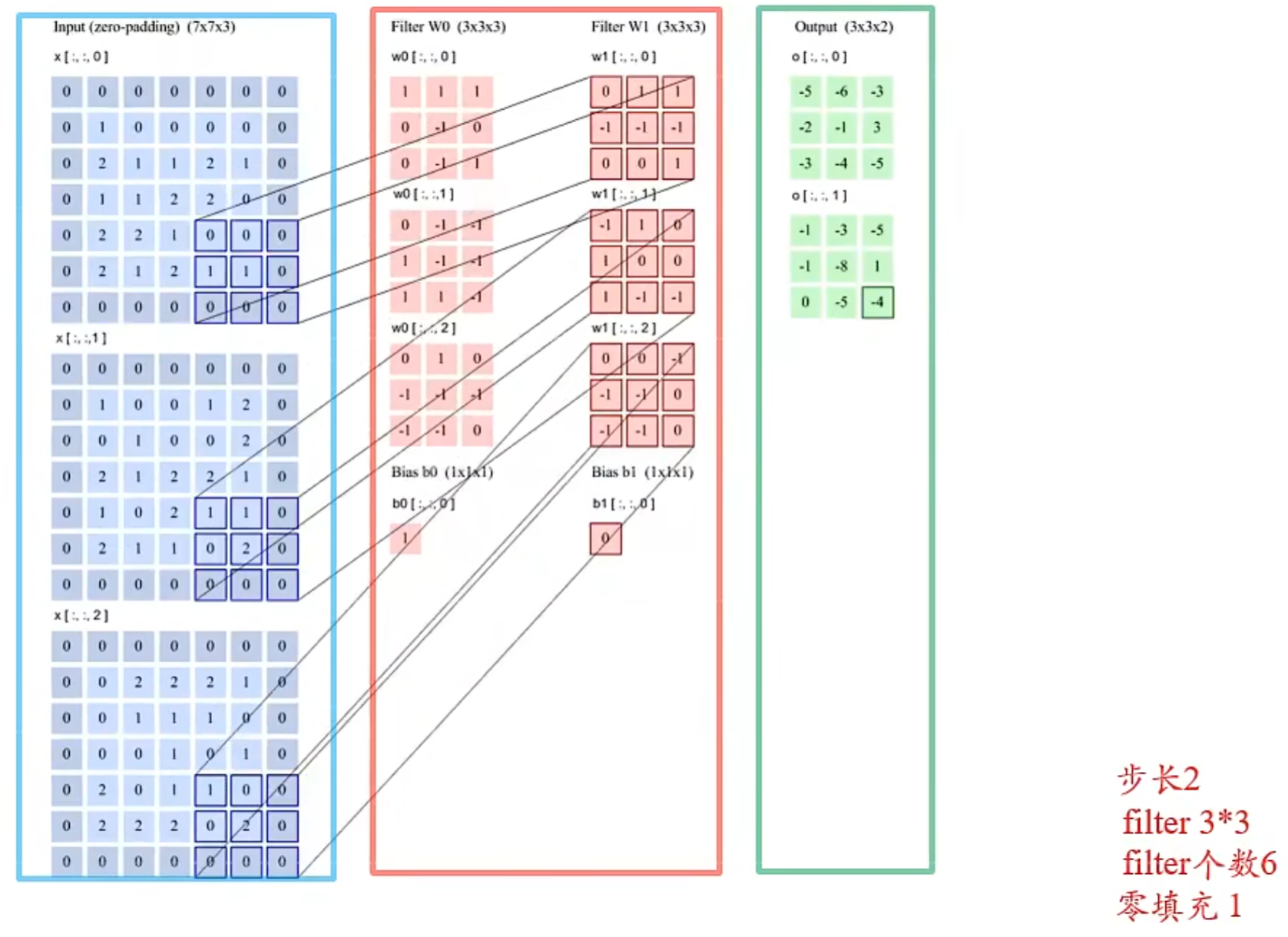
    image-20231009115107677

参数数量

每个输出特征映射都需要 $c_i$ 个卷积核，共需要 $c_o\times c_i$ 个卷积核，每个卷积核大小为 $k_h\times k_w$ 。同时，每个卷积核对应一个实数偏置，所以有 $c_o\times c_i\times k_h\times k_w+c_o\times c_i$ 个参数需要存储与学习

池化层

池化层直观上的作用是减少神经元数量，可以缓解卷积层对位置的敏感性

  • 减少输出层神经元数量：
    • 一维卷积：$M_l=M_{l-1}-(K-1)$ ，即减少 $K-1$ 个神经元
    • 二维卷积：$m_h\times m_w=(\frac{m_{w-1}+p_w+s_w-k_w}{s_w}\times \frac{m_{h-1}+p_h+s_h-k_h}{s_h})$

池化（汇聚）指对每个区域采样，用一个具有代表性的值代替这个区域

池化层也称为子采样层，作用是进行特征选择，降低特征数量，从而减少参数数量

通常处理图像时，我们希望逐渐降低隐藏在图像中的空间信息、聚集信息，随着网络层数的加深，每个神经元的感受野就越大

而机器学习的学习任务与全局图像有关，即最后一层的神经元其感受野应该是全局图像。从底层到深层，应该是从局部信息到全局信息逐渐聚合的过程，最终可以实现全局的学习目标。

在检测底层的特征时，我们通常希望在这些局部特征保持一定程度上的平移不变性。即随着拍摄角度的移动，同一个局部特征不可能发生在所有图片的同一像素位置上

image-20240327161718993

池化层窗口

池化层输入 $\mathbf{X}\in \mathbb{R}^{c_i\times n_h\times n_w}$ ，对于一个通道的输入 $[\mathbf{X}]_d,d\in [1,c_i]$ ，池化层窗口 $[\mathbf{R}]_{d}\in \mathbb{R}^{r_w\times r_h},(r_h,r_w)\in [n_h,n_w]$ 可将一个通道的输入划分为多个小区域分别进行池化

这些区域可以重叠，也可以不重叠

默认情况：池化层窗口当前扫过的区域，与下一次扫过的区域没有重叠部分，即步幅和窗口大小相等 $s_w=r_w,s_h=r_h$

最大池化层

对于一个区域 $[\mathbf{R}]_d$ ，选择这个区域中最大的元素作为这个区域的代表

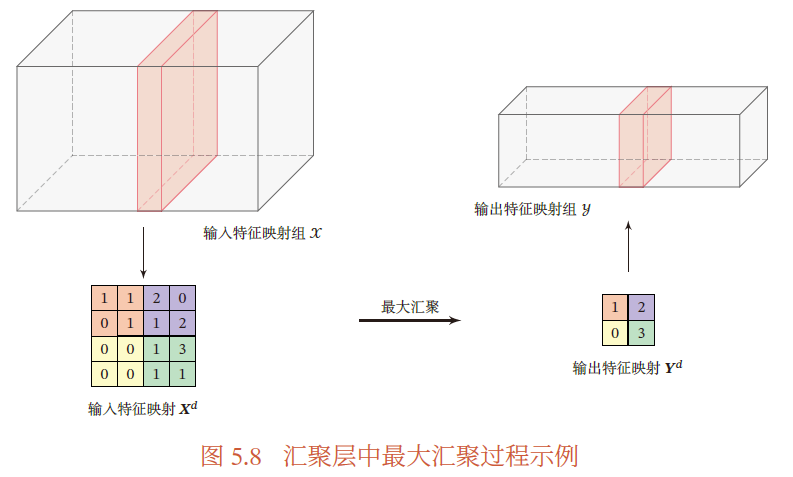
image-20231009154417166

最大池化层对卷积层位置敏感的降低

image-20240327163411660

对垂直边缘的检测， $2\times 2$ 的池化层容忍1个像素的向左(右)偏移：即一些数据 $[\mathbf{X}]_{i,j}$ 是边缘，当另一数据边缘移动到 $[\mathbf{X}]_{i,j-1}$ ($[\mathbf{X}]_{i,j+1}$)，池化层的 $[\mathbf{X}]_{i,j}’$ 仍会被认为是边缘

平均池化

对于一个区域 $[\mathbf{R}]_d$ ，选择这个区域的平均指标作为这个区域的代表

池化核

目前，主流的卷积网络仅包含 下采样 操作，但在一些早期卷积网络（LeNet-5），有时也会在汇聚层使用非线性激活函数

典型的池化层将每个特征映射划分为 $2\times 2$ 大小的不重叠区域，使用最大汇聚方式采样

  • 过大的采样区域会造成神经元数量减少过多，从而造成较多的信息损失

image-20240327174510978

最大池化层：输出每个窗口中最强的信号，在较强信号周围的像素也会受到这个强信号的影响，会有明显的层次化信息

平均池化层：对信号有一定抹平效果，信号强度小于最大池化层，有柔和作用

实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import torch
from torch import nn
from d2l import torch as d2l

def pool2d(X, pool_size, mode='max'):
    r_h, r_w = pool_size
    Y = torch.zeros((X.shape[0] - r_h + 1, X.shape[1] - r_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + r_h, j: j + r_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + r_h, j: j + r_w].mean()
    return Y
1
2
3
4
5
6
7
8
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))
#	tensor([[4., 5.],
#	        [7., 8.]])

pool2d(X, (2, 2), 'avg')
#	tensor([[2., 3.],
#	        [5., 6.]])
池化层超参数

池化层也能通过修改填充和步幅改变输出形状

1
2
3
4
5
6
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X
#	tensor([[[[ 0.,  1.,  2.,  3.],
#	          [ 4.,  5.,  6.,  7.],
#	          [ 8.,  9., 10., 11.],
#	          [12., 13., 14., 15.]]]])

默认情况下，步幅与窗口大小相等

池化层窗口大小为3，步幅也为3，所以输出窗口为 $\frac{4+3-3}{3}=1$

1
2
3
pool2d = nn.MaxPool2d(3)
pool2d(X)
#	tensor([[[[10.]]]])

自定义步幅与填充：输出 $\frac{4+1+2-3}{2}=2$

1
2
3
4
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
#	tensor([[[[ 5.,  7.],
#	          [13., 15.]]]])

也可以修改池化层窗口大小，$\frac{4-2+0+2}{2}=2$ ，$\frac{4-3+3+1}{3}=2$

1
2
3
4
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)
#	tensor([[[[ 5.,  7.],
#	          [13., 15.]]]])

多输入通道

在处理多输入通道的数据时，池化层在每个通道上单独运算，池化层的输出通道数与输入通道数相同

1
2
3
4
5
6
7
8
9
10
11
12
#构建两个通道的输入X和X+1
X = torch.cat((X, X + 1), 1)
X
#	tensor([[[[ 0.,  1.,  2.,  3.],
#	          [ 4.,  5.,  6.,  7.],
#	          [ 8.,  9., 10., 11.],
#	          [12., 13., 14., 15.]],
#	
#	         [[ 1.,  2.,  3.,  4.],
#	          [ 5.,  6.,  7.,  8.],
#	          [ 9., 10., 11., 12.],
#	          [13., 14., 15., 16.]]]])

对2输入通道的数据进行池化，输出通道仍是2

1
2
3
4
5
6
7
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)
#	tensor([[[[ 5.,  7.],
#	          [13., 15.]],
#	
#	         [[ 6.,  8.],
#	          [14., 16.]]]])

卷积神经网络的整体结构

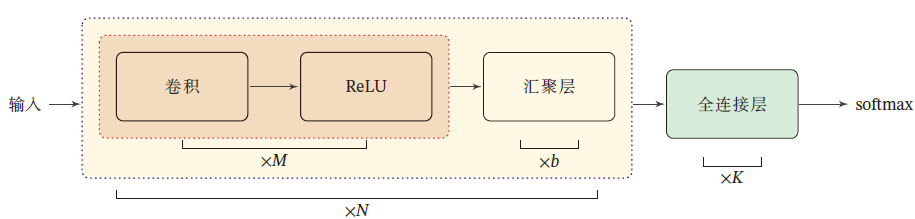
image-20231009173440863

一个 卷积块 为连续 $M$ 个卷积层和 $b$ 个汇聚层组成（一般情况，$m为2\sim 5$，$b\in\{0,1\}$）

一个卷积神经网络会连续堆叠 $N$ 个卷积块，拼接为 $K$ 个全连接层，最后 softmax 归一化

典型结构：

  • 小卷积，大深度
  • 趋向于全卷积：由于卷积操作越来越灵活（不同的步长），池化层的作用正在变小

6.3.2 参数学习

卷积神经网络中，参数为卷积核及其偏置，只需要计算卷积层中参数的梯度

参数求解目标

第 $l$ 层卷积层的输入为 $\mathbf{X}_{l}\in\R^{c_i\times n_h\times n_w}$ ，通过卷积运算得到第 $l$ 层的净输出，即第 $l$ 卷积层

第 $l$ 层有 $c_o\times c_i$ 个卷积核和偏置，每个卷积核有 $k_h\times k_w$ 个参数，即每一层共有 $c_o\times c_i\times (k_h\times k_w+1)$ 个参数需要学习

采用交叉熵损失函数

若有 $N$ 个训练数据，则结构风险函数为

参数学习的核心是梯度的学习，即求解 $\frac{\partial \mathcal{R}\left([\mathbf{W}]_{p,d}^{(l)},[\mathbf{B}]_{p,d}^{(l)}\right)}{\partial [\mathbf{W}]_{p,d}^{(l)}}$ ，$\frac{\partial \mathcal{R}\left([\mathbf{W}]_{p,d}^{(l)},[\mathbf{B}]_{p,d}^{(l)}\right)}{\partial [\mathbf{B}]_{p,d}^{(l)}}$

卷积梯度

假设 $\mathbf{H}=\mathbf{W}* \mathbf{X}\in \mathbb{R}^{(n_h-k_h+1)\times (n_w-k_w+1)}$ ，其中 $\mathbf{X}\in \mathbb{R}^{n_h\times n_w}$ ，$\mathbf{W}\in \mathbb{R}^{k_h\times k_w}$ ，有特征映射 $f(\mathbf{H})\in \mathbb{R}$ 为标量，$f(\cdot)$ 为非线性激活函数

  • 互相关结果的每个元素 $[\mathbf{H}]_{i,j}$ 与每一卷积核元素 $[\mathbf{W}]_{a,b}$ 有关所以对卷积核某一元素求偏导，是所有输出元素对该元素求偏导的核

所以 $f(\mathbf{H})$ 关于 $\mathbf{W}$ 的梯度为 $\mathbf{X}$ 与 $\frac{\partial f(\mathbf{H})}{\partial \mathbf{H}}$ 的互相关运算

  • 当使用 $[\mathbf{X}]_{i+a-1,j+b-1}$ 这个数据时，其相应的卷积核元素为 $[\mathbf{W}]_{a,b}$ ，所以当 $\begin{cases}i+a-1=s\\j+b-1=t\end{cases}$ ，$\begin{cases}a=s-i+1\\b=t-j+1\end{cases}$

  • $\mathbf{W}$ 的高上限为 $k_h$ ，但 $s-i+1$ 的上限为 $n_h$ ；$\mathbf{W}$ 的高下限为 $1$ ，但 $s-i+1$ 的下限为 $1-(n_h-w_h+1)+1=1-(n_h-k_h)$ 。

    所以，当 $(s-i+1)<1$ 或 $(s-i+1)>k_h$ ，$(t-j+1)<1$ 或 $t-j+1>k_w$ 时，$[\mathbf{W}]_{s-i+1,t-j+1}=0$ ，相当于对 $\mathbf{W}$ 进行了 $(2(n_h-k_h),2(n_w-k_w))$ 的零填充

即 $f(\mathbf{H})$ 关于 $\mathbf{X}$ 的梯度为 $\mathbf{W}$ 与 $\frac{\partial f(\mathbf{H})}{\partial \mathbf{H}}$ 的宽卷积

卷积层误差项反向传播

误差反向传播中，讨论的是：

img

根据卷积求导公式，有

即在卷积神经网络中，第 $l$ 层参数的梯度依赖于所在层的误差项 $\delta^{(l)}_p$

由于第 $l+1$ 层的输入 $\mathbf{X}^{(l+1)}$ 为第 $l$ 层的活性值 $f_l\left(\mathbf{H}^{(l)}\right)$ ，即有第 $l+1$ 层输入的第 $p$ 个元素等于第 $l$ 层净输出的第 $p$ 个元素

故：

  • $f_l’\left([\mathbf{H}]^{(l)}_p\right)$ 为 $c_o\times c_o$ 的对角矩阵，对角线元素为 $f_l’\left([\mathbf{H}]^{(l)}_1\right),\cdots,f_l’\left([\mathbf{H}]^{(l)}_{c_o}\right)$

  • 已知(PS:见《全连接层#误差的反向传播算法》)

    其中，$\mathbf{h}_l$ 为第 $l$ 层活性值，即对活性值的求导，每一个元素都需要第 $l+1$ 层的 $M_{l+1}$ 个元素累加 $\sum\limits_j^{M_{l+1}}$

    由于 $[\mathbf{X}]^{(l+1)}_p=f_l\left([\mathbf{H}]_p^{(l)}\right)$ 为第 $l$ 层的活性值，所以有

综上，卷积层误差项为

池化层误差项反向传播

当第 $l+1$ 层是池化层时，因为池化层是下采样操作，第 $l+1$ 层的误差项 $\delta$ 对应于第 $l$ 层相应特征映射的一个区域

第 $l$ 层的第 $p$ 个特征映射中的每个神经元都有一条边和 $l+1$ 层的第 $p$ 个特征映射中的一个神经元相连

第 $l$ 层第 $p$ 个特征映射的误差项 $\delta^{(l)}_p$ 的具体推导为

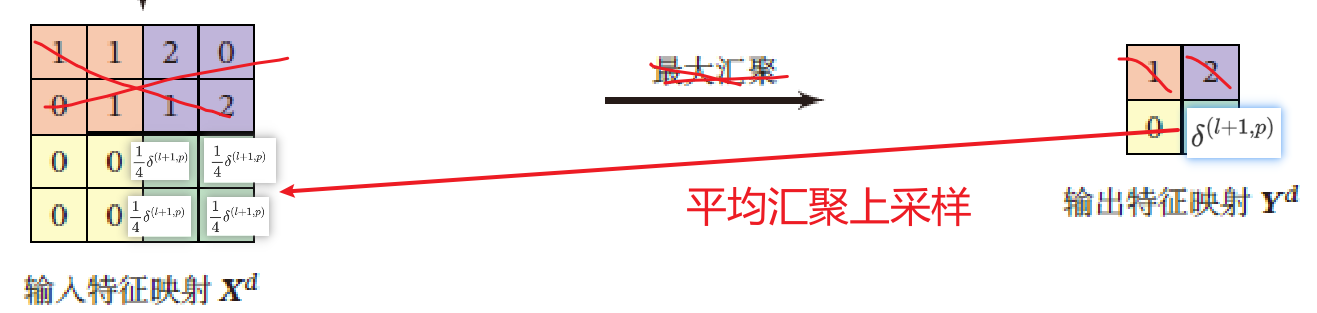
$up(\cdot)$ 为上采样函数，与汇聚层的下采样操作相反

  • 若下采样是最大汇聚，则 $\delta^{(l+1)}_p$ 中每个值会直接传递到前一层对应区域中的最大值对应的神经元，该区域中其他神经元设为0

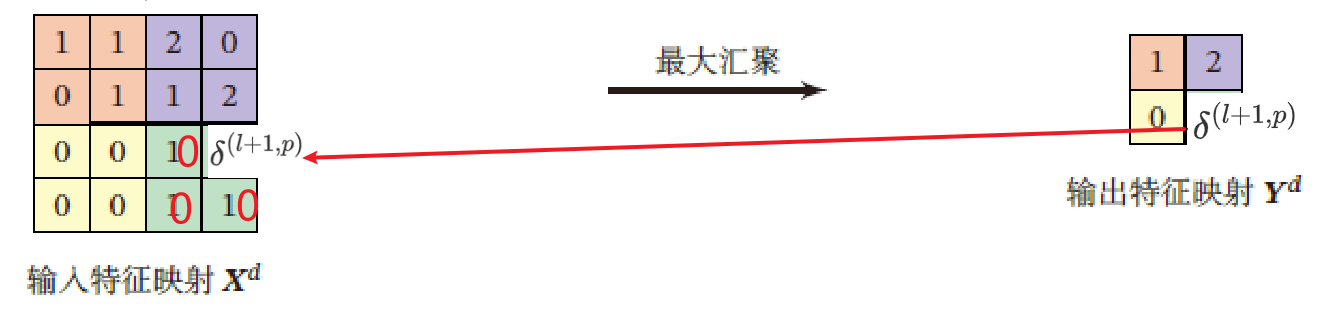
    image-20231011104226007

  • 若下采样是平均汇聚，则误差项 $\delta^{(l+1)}_p$ 中每个值被平均分配到前一层对应区域的所有神经元上

    image-20231011110019384

-------------本文结束-------------