AmosTian

0%

4.图

发表于 更新于 分类于 >
本文字数 4.2k字 | 阅读时长 ≈ 8 分钟

图这部分以概念为主，具体实现放到算法部分

参考：王道数据结构图部分

4.1 基本概念

不存在空图

  • 顶点集一定非空

  • 边集可以为空

图和树是逻辑上的区别，都是 逻辑结构

4.1.1 顶点的度

4.1.2 图的种类

1. 简单图

  • $v_i \rightarrow v_j$ 间无重复边
  • 任一顶点无自身到自身的顶点

2. n个顶点的完全图

3. 子图

顶点集为图G的子集

  • 并非所有的顶点子集与边子集的组合都是图G的子图
  • 任一条边及其两个端点都在的边集与顶点集的组合才构成子图

4. 连通图[无向图]

无向图连通：顶点 $v\rightarrow w$ 直接有路径

图 G 中任两顶点间都连通

  • 一点可以访问全部
  • 若边数小于n-1，则一定是非连通图
  1. 连通分量：无向图中极大连通子图
  2. 生成树：连通图 的包含所有结点的极小连通子图
    • 包含n-1条边，n个顶点
    • 加一条边构成回路，减一条边为非连通图
  3. 生成森林：非连通图 的多个连通分量生成的多个树构成的森林

5. 路径&完全图

路径

$v_p \rightarrow v_q$ 之间的顶点序列

  • 路径长度：路径中的顶点个数
  • 距离：$v_p \rightarrow v_q$ 的最短路径长度
  • 简单路径：顶点不重复

回路、环：起点和终点 ($v_p == v_q$) 相同的路径

  • 简单回路：除首尾顶点不重复的路径
  • 有拓扑序列的图一定无环
完全图

已知有n个顶点，确保连通的的最小边数为：n-1个顶点的完全图的边数+1,$\frac{(n-1)(n-2)}{2}+1$

已知有n条边，组成非连通图的顶点数为：k个顶点组成完全图+1,$\frac{k(k-1)}{2}+1\Rightarrow \lceil \sqrt{2n} \rceil+1$

6. 强连通图[有向图]

有向图连通：$v \rightleftarrows w$ ，双向连通

每对顶点间有 路径

  • 不是每对顶点间都有 弧

  1. 强连通分量

    有向图中的极大强连通图

  2. 有向完全图一定是强连通图

4.2 图的存储

4.2.1 邻接矩阵法

1. 规则

  1. 表示

  1. 无向图

    • 邻接矩阵对称且唯一

    • 可进行压缩存储，只存放上(下)三角矩阵元素

      对称矩阵默认为无向图

    • 第i行(列)非零元素个数= $v_i$ 的出度OD( $v_i$ )或者入度ID( $v_i$ )

  2. 有向图

    • 第i行非零且非 $\infty$ 的元素个数为顶点 $v_i$ 的出度
    • 第i列非零且非 $\infty$ 的元素个数为顶点 $v_i$ 的入度

2. 特点

  1. 适用于 稠密图 存储

  2. 空间复杂度为 $O(\mid v\mid^2)$

  3. 确定两点之间是否有边 $O(1)$ ——数组的随机存取特性

    确定图中边数 $O(\mid v\mid^2)$

  4. 某个顶点出度越大，则存储矩阵的行非零元素越多

  5. 图G的邻接矩阵为A，则$A^n[i][j]$ 表示从 $v_i \rightarrow v_j$ 的长度为n的路径数量

#### 3. 表示
1
2
3
4
5
typedef struct{
    VexType Vex[MaxVertexNum];//顶点集
    EdgeType Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵表示边集
    int vexnum,arcnum;
}MGraph;
#### 4. 有向无环图的矩阵表示 > 有向无环图：非零元素集中在上三角或下三角区域，其对称区域全为0 - 图中比不存在环 - 一定存在拓扑序列但不唯一 上三角：出度大编号小 下三角：入度大编号小 ### 4.2.2 邻接表法 邻接表法：只存出度 逆邻接表法：只存入度 > 邻接表：每个顶点 v 建立相应的边表 > > - 顶点头指针(**顺序存储**) ：顶点头指针为边链表的头指针，指向与 $v_i$ 关联的首条边 > > - 边信息(**单链表**) > > 无向图：依附于 $v_i$ 的边 > > 有向图：以 $v_i$ 为尾的弧

1. 特点

  1. 适用于 稀疏图

  2. 邻接表 不唯一

    同一顶点的边结点连接顺序不唯一，取决于建立边表的算法及边的输入序列

  3. 存储空间

    无向图：$O(\mid v\mid+2\mid e\mid)$

    有向图：$O(\mid v\mid+\mid e\mid)$

  4. 时间复杂度

    找所有邻边：读顶点的边表——$O(n)$

    确定边是否存在：扫一个端点的边表—— $O(n)$

  5. 有向图某顶点的度

    出度：邻接表中结点个数

    入度：需遍历全部邻接表

2. 表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
typedef struct{
    VexType data;
    ArcNode *firstArc;
}VNode,AdList[MaxVertexNum];//邻接表

typedef struct{
    int adjvex;//邻接点域
    double weigh;//边表权值
    struct ArcNode *nextArc;//邻接顶点
}ArcNode;//边表结点

typedef struct{
    int vexnum;
    int arcnum;
    AdList vertices;//顶点头指针
}AGraph;

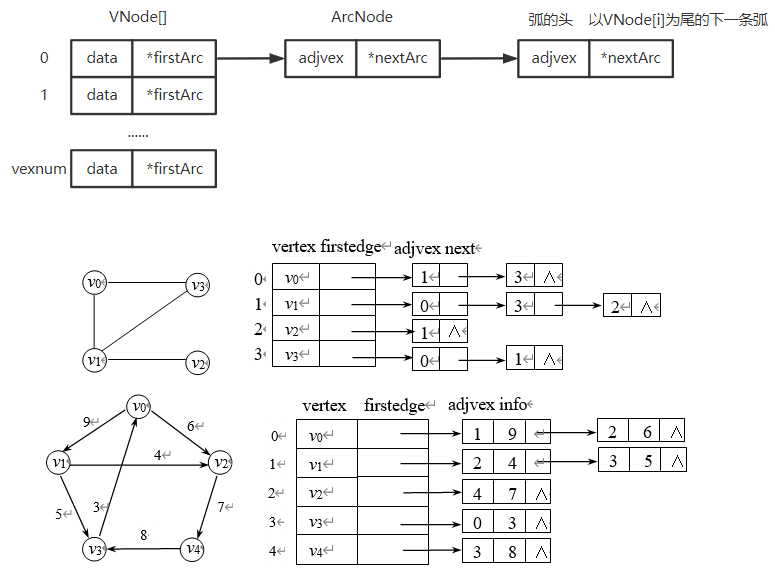
4.2.3 邻接多重表

无向图的存储结构

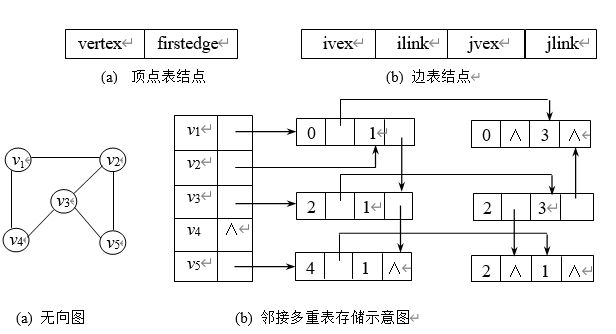
4.2.4 十字链表法

有向图的存储结构

4.3 图的基本操作

独立于存储结构

参数相同；实现不同，性能不同

1
2
3
4
5
6
7
8
9
10
Adjacent(G,x,y);//x与y之间是否存在边
Neighbors(G,x);//x的邻接边
FirstNeighbor(G,x);//G中x的第一个邻接点
NextNerghbor(G,x,y);//G中除x的下一个邻接点

InsertVertex(G,x);//插入点
DeleteVertex(G,x);//删除点

AddEdge(G,x,y);//新增边
RemoveEdge(G,x,y);//移除边

已知n个顶点的图，其邻接矩阵表示为MGraph，邻接表表示为LGraph

  1. 判别图中边数 n(e)

    n(x)：表示x的个数

无向图有向图
MGraph$n(e)=\frac{n(1)}{2}$$n(e)=n(1)$
LGraph$n(e)=\frac{n(eNode)}{2}$$n(eNode)$
  1. 判断两点是否连通
MGraph$MGraph[i][j] \overset{?}{=}1$$O(1)$
LGraph遍历顶点i的邻接表$O(e)$
  1. 度的计算
无向图有向图
MGraph$2*第 i 行 ‘1’ 的个数$出度：第 i 行 ‘1’ 的个数
入度：第 i 列 ‘1’ 的个数
LGraphn(eNode)$出度：表头为 i 的单链表中 eNode 的个数$
$入度：边表中 i 的个数$

4.3 图的遍历

从某一顶点出发，沿图中的边对图中所有顶点访问且只访问一次

  • 遍历与经过的区别

    从某一点出发经过图中所有结点 $\neq$ 遍历：每个结点不重复的访问一次

  • 对每个顶点查找邻接点的过程取决于存储结构

    矩阵： $O(\mid v\mid^2)$

    邻接表：$O(\mid e\mid)$

  • 树是一种特殊的图

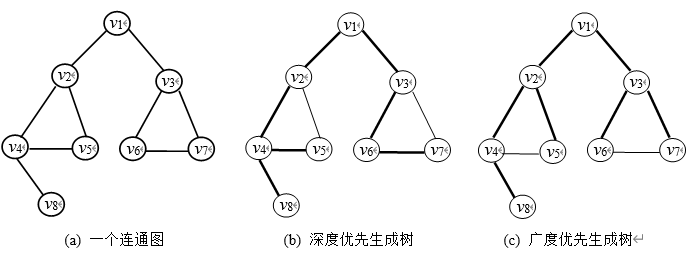
4.3.1 广度优先搜索

从某一顶点 v 开始，由近到远访问和 v 有路径长度为1,2,3….的顶点

  • 逐层访问，故需要借助队列

1. 实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
bool visted[MAX_VERTEX_NUM];

bool BFSTraverse(Graph G){
    //初始化
    for(int i = 0;i < G.vernum;++i)
        visited[i] = FALSE;
    InitQueue(Q);
    
    //BFS
    for(int i = 0;i < G.vexnum;++i)
        if(!visited[i])
            BFS(G,i);//使用for循环确保每个连通分量都被访问
}

void BFS(Graph G,int v){//从顶点v出发，广度优先遍历图G
	visit(v);
    visited[v] = TRUE;
    EnQueue(Q,v);//顶点v入队
    
    while(!isEmpty(Q)){
        DeQueue(Q,v);
        for(w = FirstNeighbor(G,v);w >= 0;
            				w=NextNeighbor(G,v,w)){
            //检测v的所有邻接点w
            if(!visited[w]){//w为v尚未访问的邻接点
                visit(w);
                visited[w] = TRUE;
                EnQueue(Q,w);
            }
        }
    }
}

2. 性能分析

  1. 空间复杂度

    $O(\mid v\mid)$

  2. 时间复杂度[与采取的存储方式有关]

    • 邻接矩阵 $O(\mid v\mid^2)$

    • 邻接表 $O(\mid v\mid+\mid e\mid)$

      顶点入队 $O(\mid v\mid)$

      搜索所有邻接点，访问边 $O(\mid e\mid)$

3. 应用

  1. 求 $u \rightarrow v$ 路径长度最小的路径

  2. 无权图求单源点最短路径

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    void BFS_Min_Distance(Graph G,int u){
        //d[i]表示从u到i的最短路径
        for(i = 0;i < G.vexnum;++i)
            d[i] = INFINITE;
        visited[u] = TRUE;
        d[u] = 0;
        EnQueue(Q,u);
        while(!isEmpty(Q)){
            DeQueue(Q,u);//BFS算法主过程
            for(w = FirstNeighbor(G,u);w >= 0;
               			w = NextNeighbor(G,u,w)){
                if(!visited[w]){
    				visited[w] = TRUE;//设已访问标记
                    d[w] = d[u]+1;
                    EnQueue(Q,w);
                }
            }
        }
    }

  3. 广度优先生成树

    邻接矩阵：表示法唯一 $\Longrightarrow$ 生成树唯一

    邻接表：表示法不唯一 $\Longrightarrow$ 生成树不唯一

4.3.2 深度优先搜索

DFS——递归算法，用一个递归工作栈，空间复杂度 $O(\mid v\mid)$

性能分析

  • 时间复杂度

    邻接矩阵 $O(\mid v\mid^2)$

    邻接表 $O(\mid v\mid+\mid e\mid)$

  • 空间复杂度

    $O(\mid v\mid)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
bool visited[MAX_VERTEX_NUM];//访问标记数组

void DFSTraverse(Graph G){
    for(v = 0;v < G.vexnum;++v) //初始化
        visited[v] = FALSE;
    for(v = 0;v < G.vexnum;++v)//遍历所有连通分量
        if(!visited[v])
            DFS(G,v);
}

void DFS(Graph G,int v){
    visit(v);
    visited[v] = TRUE;//访问v并做标记
    for(w = FirstNeighbor(G,v);w >= 0;
        			w = NextNeighbor(G,v,w)){
        if(!visited[w])
            DFS(G,w);
    }
}

4.3.3 图的遍历与连通性

  1. 连通

    • 无向图：从某一顶点 v 出发，一次遍历可访问图中所有顶点
    • 有向图：初始点到图中每个顶点都有路径

  2. 连通分量个数

  • DFSTraverse / BFSTraverse 中调用 DFS / BFS 次数为连通分量数

  1. 对一个有向无环图，DFSTraverse 的退栈序列就是一个拓扑序列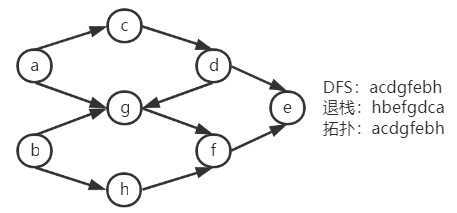

4.4 应用

4.4.1 最小生成树

  1. 边数 = 顶点数 - 1

  2. 带权连通图权值和最小

    最小权值和唯一，但树形不唯一

    若各边权值互不相等，则树形唯一

1
2
3
4
5
6
Generate_MST(Graph G){
    T = NULL;
    while T未形成树
        do 找最小代价边(u,v)且加入T后不形成回路
    		T = T ∪ (u,v);
}

1. 深度优先、广度优先生成树

2. Prim算法

选点：Prime——Point

手动模拟

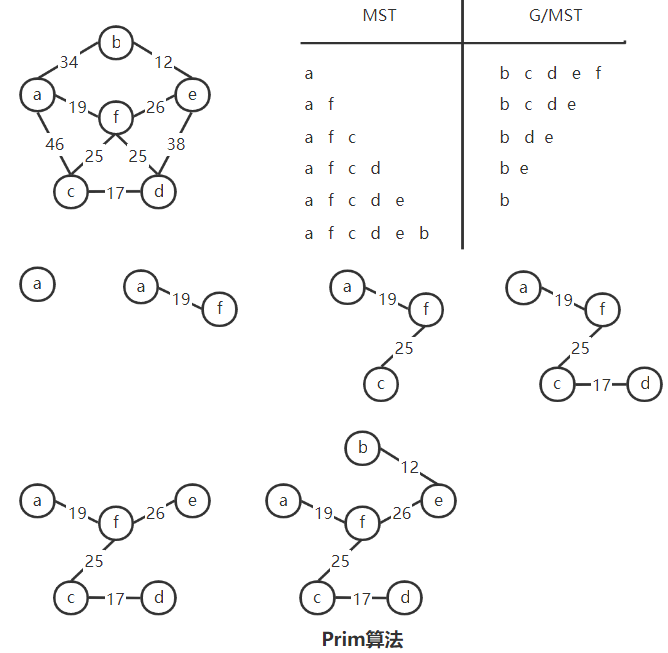
实现

1
2
3
4
5
6
7
8
9
void Prim(G,T){
    T = ∅;//初始化为空集
    U = {'a'};//MST的顶点集
    while((V-U) != ∅){
        设(u,v)是使 u∈U与v∈V，且权值最小的边;
        T = T∪{(u,v)};
        U = U∪{v};
    }
}

时间复杂度：$O(\mid v\mid^2)$ ，故不依赖于边集，适用于稠密图

3. Kruskal算法

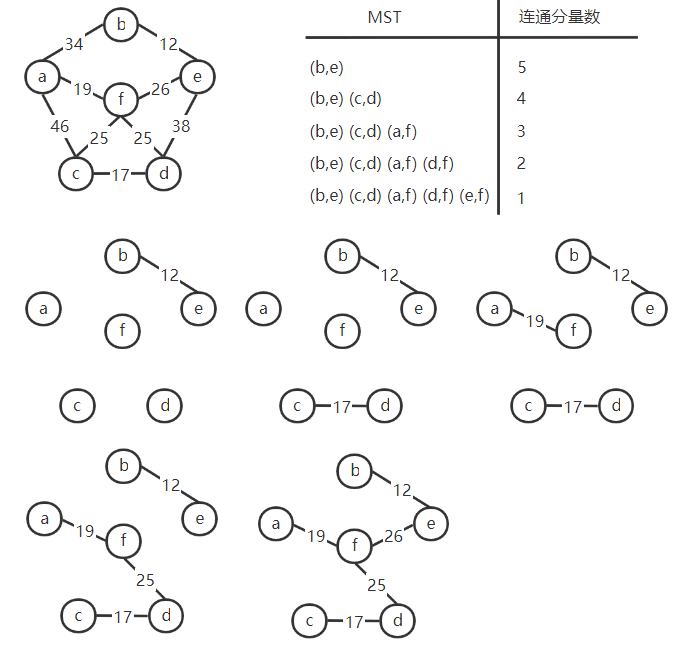
image-20220203114520778

1
2
3
4
5
6
7
8
9
10
11
void Kruskal(G,T){
    T = V;//初始化树，仅含顶点
    numS = n;//连通分量数
    while(numS > 1){//若连通分量数大于1
        从E中取出权值最小的边(v,w);
        if(v和u属于不同连通分量){
            T = T∪{(v,u)};//将此边加入生成树中
            numS--;
        }
    }
}

时间复杂度：$O(\mid e\mid log\mid e\mid)$ ，适用于点多边少

4.4.2 最短路径

带权路径长度：路劲上权值的和

  • 满足连通的 $u \rightarrow v$
  • 找所有 $u \rightarrow v$ 中权值最小的路径

区别：

Dijkstra : 单源点最短路径

Floyd : 多源点最短路径

1. Dijkstra

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
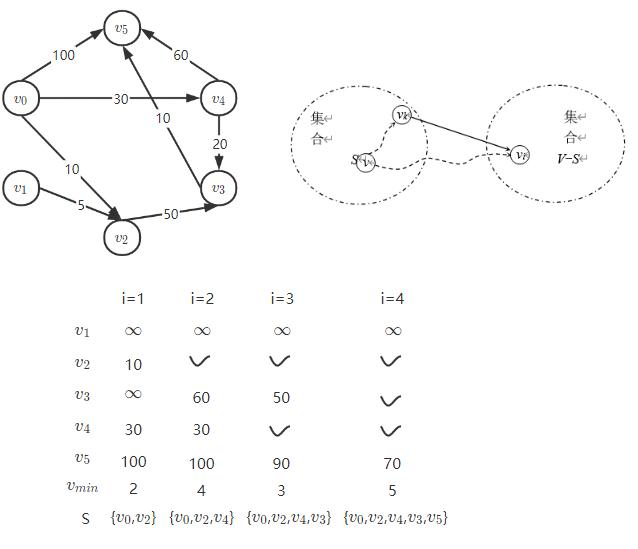
25
void Dijkstra(MGraph G,int v0,Patharc P,ShortPathTable D){
	int flag[MAXVEX];//访问标记数组 0-未访问 1-已访问 
	for(int i = 0;i < G.numVertices;++i){
		flag[i] = 0;
		D[i] = G.arc[v0][i];//D[]为距离数组 
		P[i] = 0;//P[i]为到达vi的路径长度 
	} 
	D[v0] = 0,flag[v0] = 1,P[0] = 0;
	
	for(int i = 0;i < G.numVertices;++i){
		int min = INFINITY;//记录当前距离最小值 
		int idx;//记录距离最小值下标 
		for(int j = 0;j < G.numVertices;++j)//查找距离v0最近的点 
			if(!flag[j] && D[j] < min){//vj未被访问且距离最小 
				idx = j;
				min = D[j];
			}
		
		flag[idx] = 1;
		for(int w = 0;w < G.numVertices;++w)//更新各顶点最小距离 
			if(!flag[w] && (min + G.arc[idx][w] < D[w]))
				D[w] = min + G.arc[idx][w]; 
		P[i+1] = idx;
	} 
}

2. Floyd

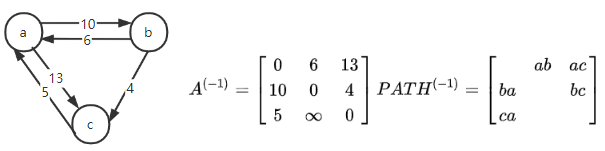
4.4.3 有向无环图

有向无环图：一个有向图中无环，简称DAG

用于描述公共子式

  • 符号最多为二元运算符
  • 出现多少种运算数就多少个叶结点

4.4.4 拓扑排序

在一个有向无环图的顶点组成的序列中

  • 每个顶点出现且只出现一次

  • 若顶点A在序列中排在顶点B前面，则在图中不存在B->A的路径

    对有向无环图的一种排序，若存在一条顶点A到顶点B的路径，则在排序中顶点B出现在顶点A的后面。

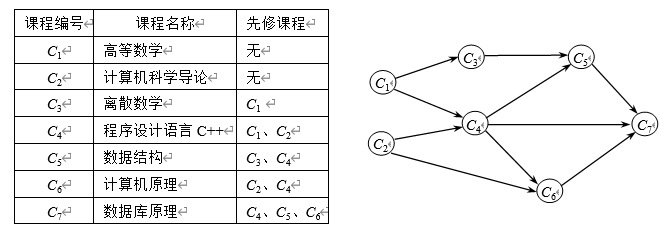
1. AOV

AOV(用顶点表示活动)：若用DAG表示一个工程，顶点表示活动，有向边 $$ 表示活动 $v_i$ 必须先于活动 $v_j$ 发生的关系。

  • $v_i$ 是 $v_j$ 的直接前驱，$v_j$ 是 $v_i$ 的直接后继，具有传递性
  • 任何活动 $v_i$ 都不能以自身作为前驱或者后继

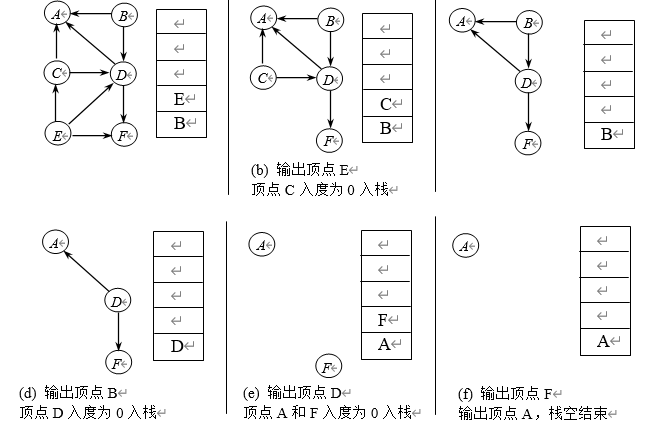
2. 拓扑排序步骤

  1. 每次从AOV中选一个没有前驱(入度=0)的顶点输出

  2. 从AOV网中删除该顶点和以该顶点为起点的所有边

  3. 重复 1. 2. 直至当前的AOV为空或当前网中不存在无前驱的顶点

    若AOV为空，则该图存在拓扑序列

    若AOV不空，则该图不存在拓扑序列

3. 拓扑排序实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
bool TopologicalSort(Graph G){
    InitStack(S);//初始化栈，存储入度为0的顶点
    for(int i = 0;i < G.vexnum;++i)
        if(indegree[i] == 0)
            Push(S,i);//将所有入度为0的顶点入栈
    
    int count = 0;//表示已经输出的顶点数
    while(!IsEmpty(S)){
        Pop(S,i);//栈顶元素出栈
        print[count++] = i;//输出顶点i
        for(p = G.vertices[i].firstarc;p;p = p->nextarc){
            //将所有i指向的顶点入度减1并将入度为0的顶点压栈
            v = p->adjvex;//v是p的邻接点
            if(!(--indegree[v]))
                Push(S,v);//入度为0则入栈
        }
    }
    if(count < G.vexnum)
        return false;//排序失败，有向图有回路
    else
        return true;//存在拓扑序列
}

  • 时间复杂度：$O(\mid v\mid+\mid e\mid)$

  • 入度为零的顶点，即没有前驱活动的或前驱活动全部完成的顶点，工程可以从这个顶点所代表的活动开始或继续

  • 若一个顶点有多个直接后继，则拓扑序列不唯一
  • AOV网中各个顶点地位相同，故可重新编号，若是DAG则其邻接矩阵是三角矩阵

4.4.5 关键路径

1. AOE

有向无环图中，顶点表示事件，有向边表示活动，边上权值表示完成该活动的开销。用边表示活动的图为AOE。

  • 只有在顶点所代表的事件发生后，从该顶点出发的有向边代表的活动才能开始
  • 只有在进入某顶点各有向边所代表的活动完成后，该顶点所代表的事件才能发生
  • AOE网中，只有一个入度为0的顶点（源点），表示整个工程开始；一个出度为0的顶点（汇点），表示整个工程结束

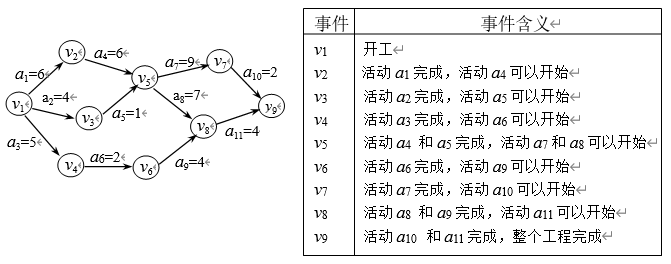
拓扑序列：$v_1,v_2,v_3,v_4,v_5,v_5,v_6,v_7,v_8,v_9$

2. 关键路径

从源点到汇点的路径中，具有最大路径长度的路径；关键路径上的活动为关键活动

  • 加快关键活动可以缩短整个工程的工期，但缩短到一定程度，关键活动会为非关键活动
  • 若AOE网中关键路径不唯一，只有加快公共的关键路径上的关键活动，才能缩短工期

3. 活动的最早开始时间最晚开始时间

活动最早开始时间 = 活动的起点事件最早开始时间

活动的最晚开始时间 = 活动的终点事件最晚开始时间-活动的时长

活动的最晚开始时间-活动的最早开始时间 = 0 的活动为关键活动

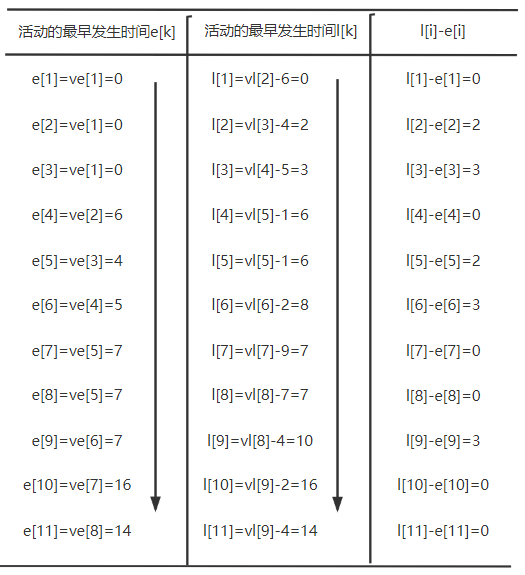
即关键路径为($v_1,v_4,v_7,v_8,v_{10},v_{11}$)

-------------本文结束-------------