[TOC]
环境
1 | import matplotlib.pyplot as plt |
策略基类
1 | class Policy: |
打印策略
1 | from typing import List |
Q-learning
1 | class QLearning(Policy): |
1 | np.random.seed(0) |
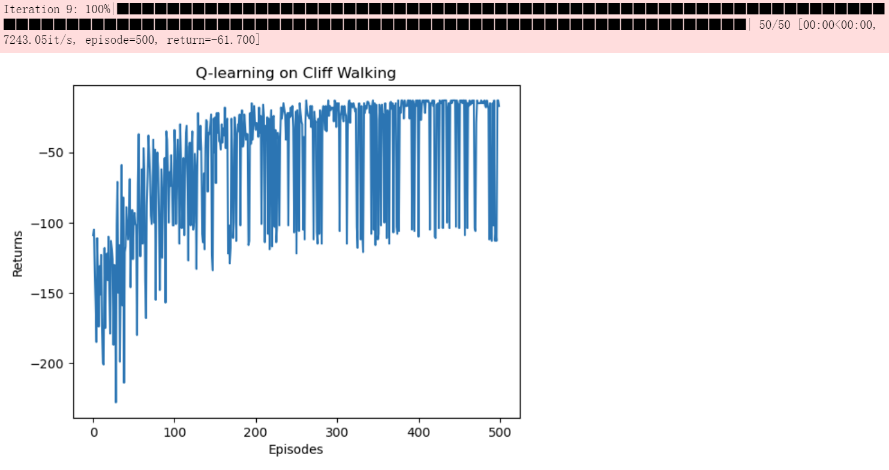

Sarsa
1 | class Sarsa(Policy): |
1 | ncol = 12 |
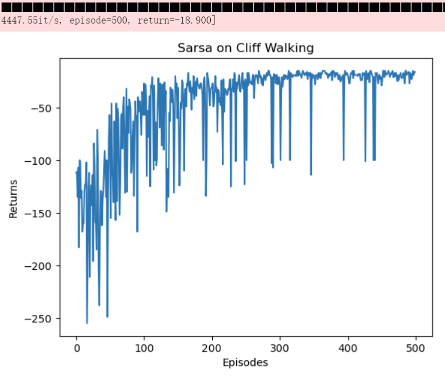

Sarsa改进
n步Sarsa
减小经典Sarsa价值估计的偏差,减小MC方算法的方差
1 | class nstep_Sarsa(Policy): |
1 | np.random.seed(0) |
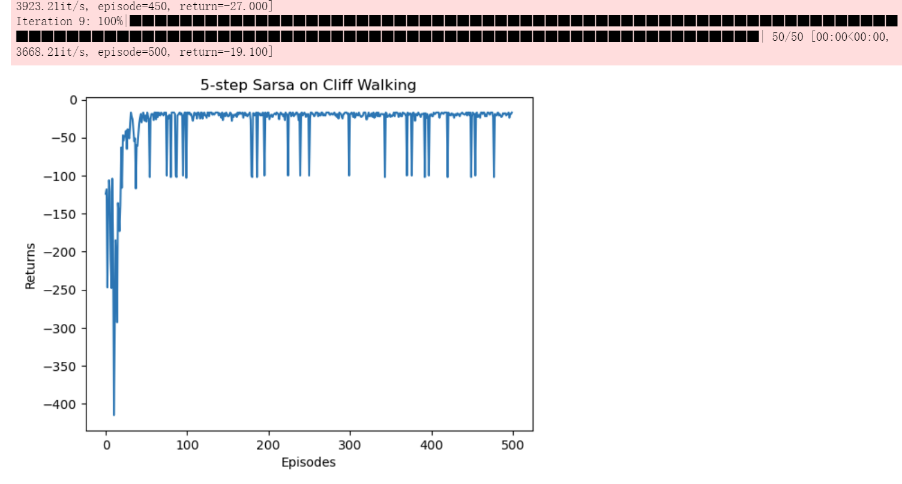
1 | action_meaning = ['^', 'v', '<', '>'] |

离线n步Sarsa
对于状态价值
为经验增加重要性权重
有轨迹
而在n步Sarsa中,
所以,$n$ 步离线的经验去估计状态价值,重要性权重为
由于重要性权重的连乘,所以是对状态价值的无偏估计,但是方差大(不同策略下的同一轨迹)
对于动作价值
在 n-step Sarsa 中,
$T$ 是终止状态的时间步
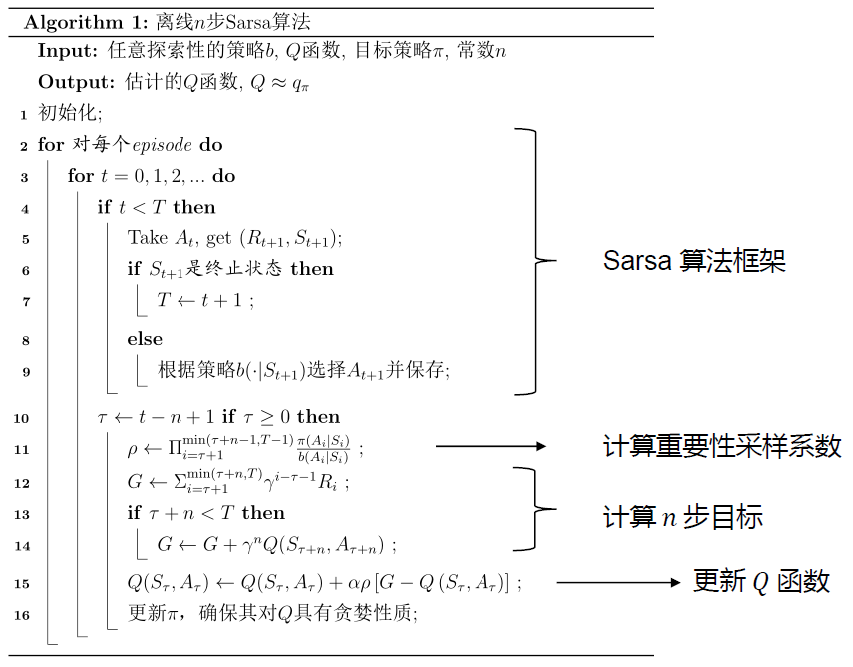
离线强化学习
多步树回溯算法
一种不需要重要性采样的离线算法
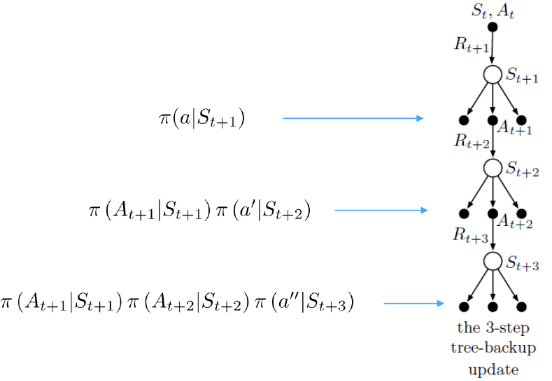
在状态 $s_t$ 下采取动作 $a_t$ ,到达状态 $s_{t+1}$ ,基于策略 $\pi(a\vert s_{t+1})$ 选择动作 $a_{t+1}$ ,获得动作价值 $Q(s_{t+1},a_{t+1})$ ,此时到达状态 $s_{t+2}$
在状态 $t+2$ 下采取动作 $a_{t+2}$ 的概率已经变为 $\pi(a_{t+1}\vert s_{t+1})\pi(a_{t+2}\vert s_{t+2})$
在 n-step 计算状态价值时
- $n=1$ ,$G_t^{[1]}=R_{t+1}+\gamma \sum_a\pi(a\vert s_{t+1})Q^{(t)}(s_{t+1},a)$
n=2
推广