AmosTian

0%

5-基于策略梯度的RL

发表于 更新于 分类于 > >
本文字数 10.6k字 | 阅读时长 ≈ 28 分钟

[TOC]

  • 策略梯度
    • 最优梯度的度量
    • 度量的梯度
  • 基于蒙特卡洛的策略梯度——REINFORCE
    • 梯度上升算法
  • AC方法
    • QAC
    • A2C：通过引入偏置量减少估计的方差
    • off-policy AC：将on-policy方法转换为 off-policy方法
      • 重要性采样
    • DPG：随机策略变为确定性策略

5.1 策略梯度

之前的方法以策略为核心，基于价值产生策略，并用表格表示策略

策略梯度 (policy gradient) 是基于策略的方法，用策略函数近似策略

利用机器学习模型的泛化能力，将已知状态上的策略泛化到未知状态上的策略

目标函数是策略的函数，通过优化目标函数直接获取最优策略

  • A-C方法，实际上是将策略梯度与价值函数结合的方法

5.1.1 策略的表示

表格型策略

策略为在每个状态下 $s\in \mathcal{S}$ 采取每个动作 $a\in \mathcal{A}(s)$ 的可能性可以用表格 $\pi(a\vert s)$ 表示，在表格中使用 $(s,a)$ 获取每个策略

$a_1$$a_2$$a_3$$a_4$$a_5$
$s_1$$\pi(a_1\vert s_1)$$\pi(a_2\vert s_1)$$\pi(a_3\vert s_1)$$\pi(a_4\vert s_1)$$\pi(a_5\vert s_1)$
$\vdots$$\vdots$$\vdots$$\vdots$$\vdots$$\vdots$
$s_9$$\pi(a_1\vert s_9)$$\pi(a_2\vert s_1)$$\pi(a_3\vert s_1)$$\pi(a_4\vert s_1)$$\pi(a_5\vert s_1)$

缺点：当状态空间很大或无穷、状态连续变化时，用表格表示策略就非常低效，体现在存储与泛化能力的缺陷上

函数型策略

用带参数的函数拟合策略，也可以表示为 $\pi_{\theta}(a\vert s),\pi(a,s,\theta),\pi_{\theta}(a,s)$

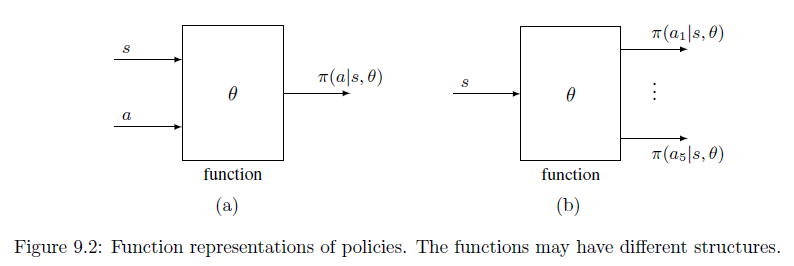
image-20240307100321679

(a) 输入是状态和动作，输出是当前状态下采取这个动作使累积奖励最大化的可能性

(b) 输入是状态，输出是当前状态下采取各个动作使累积奖励最大化的可能性

最优的策略可以通过最优化度量标量的目标函数获取，这种方法称为 策略梯度

  • 更适合处理高维度或连续的动作空间
  • 具有更强大的泛化能力
  • 具有更好的收敛性质和稳定性
  • 能够学习随机策略

缺点：

  • 通常会收敛到局部最优，而非全局最优，所以需要加噪音扰动
  • 评价一个策略通常不高效，且方差较大（受数据分布影响大，策略一直变，所以数据分布一直变）

表格型VS函数型

最优策略的定义：

  • 表格型：若一个策略 $\pi^$ 使每个状态价值都是最大的，即 $\mathbf{V}_{\pi^}(S)\ge\mathbf{V}_{\pi}(S),\forall \pi\in \Pi$
  • 函数型：指定一个标量的策略度量指标目标函数，使目标函数最大化的策略就是最优策略

获取一个动作的概率：

  • 表格型：通过 $(s,a)$ 可查表获取

  • 函数型：计算策略函数的值 $\pi(a\vert s,\theta)$

    参数每传播一次，都需要计算一次

策略更新：

  • 表格型：直接修改 $\pi(a\vert s)$ 的值
  • 函数型：通过修改策略函数的参数 $\theta$ 间接影响策略

策略梯度基本思路

所有的策略度量指标 $J(\pi)$ 都是 $\pi$ 的函数，而 $\pi(a\vert s,\theta)$ 是关于参数 $\theta$ 的函数 ，不同的参数值 $\theta$ 会影响策略优劣的度量值，因此，通过最优化 $\theta$ 的值来最大化这些度量指标，可以找到最优的策略

最优化算法为梯度上升法

  • 如何定义策略度量指标
  • 如何计算策略度量指标的梯度

5.1.2 策略度量指标

平均状态价值

  • $\overline{V}_{\pi}$ 为在策略 $\pi$ 下加权平均的状态价值
  • $d(s)\ge 0,\sum\limits_{s\in \mathcal{S}}d(s)=1$ 是状态 $s$ 的权重，也可以理解为状态的概率分布 $S\sim d$
  • 向量形式下，$\mathbf{d}=\begin{bmatrix}\vdots\\d(s)\\\vdots\end{bmatrix}\in \R^{\vert \mathcal{S}\vert},\mathbf{V}_{\pi}=\begin{bmatrix}\vdots\\V_{\pi}(s)\\\vdots\end{bmatrix}\in\R^{\vert \mathcal{S}\vert}$

若求解加权平均，需要知道状态 $S$ 服从的分布 $d$

$d$ 与策略 $\pi$ 无关

将分布 $d$ 记为 $d_0$ ，此时，平均状态价值记为 $\overline{V}_{\pi}^0$

相对简单，因为度量指标函数的梯度计算相对简单

一种情况是每个状态都是同等重要的，因此将 $d_0$ 视为均匀分布，$d_0(s)=\frac{1}{\vert \mathcal{S}\vert}$

另一种情况是只关注特定的状态 $s_0$ ， 如在一些任务中所有回合都从相同的起始状态 $s_0$ 出发，实际上就是最大化从 $s_0$ 出发得到的回报，因此 $d_0(s_0)=1,d_0(s\neq s_0)=0\Rightarrow\overline{V}_{\pi}=V_{\pi}(s_0)$

$d$ 与策略 $\pi$ 有关

状态的分布与策略 $\pi$ 有关，即 $d$ 是策略 $\pi$ 下的稳态分布

  • 状态分布概率值是状态转移矩阵特征值为1的特征向量

平均单步立即奖励

其中，$r_{\pi}(s)=\sum\limits_{a\in \mathcal{A}(s)}\pi(a\vert s,\theta)r(s,a)$ ，$r(s,a)=E[R\vert s,a]=\sum\limits_{r’}r’P(r’\vert s,a)$

两种度量指标的关系

关于策略的度量指标，可以定义在折扣奖励 $\gamma \in [0,1)$ 下，也可以定义在非折扣奖励 $\gamma=1$ 下

对于 平均单步立即奖励 $\overline{r}_{\pi}$ ，只是对立即奖励的平均，不求回报所以也不需要考虑折扣因子，此时 $\gamma=1$

$\overline{r}_{\pi}$ 是一种非常短视的度量指标，只考虑立即奖励，相反，$\overline{V}_{\pi}$ 是一种相对远视的度量指标，考虑到所有步的总奖励，虽然二者不相等，但成正比

一个达到最优，另一个也能达到极值

证明：贝尔曼方程 $V_{\pi}=r_{\pi}+\gamma P_{\pi}V_{\pi}$ ，两边同乘 $d^T_{\pi}$

等价定义

image-20240312103943638

平均状态价值

在策略 $\pi$ 下有从状态 $S_0$ 开始的轨迹 $(A_{0},R_{1},S_1,A_1,R_2,\cdots)$ ，满足 $A_{t}=\pi(S_t,\theta)$ ，$R_{t+1},S_{t+1}\sim P(R_{t+1},S_{t+1}\vert S_t,A_t)$

对于

平均单步立即奖励

假设在策略 $\pi$ 下生成了起始状态为 $s_0$ 的轨迹，奖励序列为 $\{R_{t+1}\}_{t=0}^\infty$，这个轨迹的平均单步奖励为

  • 起始状态 $s_0$ 是什么不重要

证明：

首先，证明对于任意的起始状态 $s_0$ ，有第一个等号成立

  • 纬洛平均：对于一个序列 $\{a_k\}_{k=1}^{\infty}$ 若其是收敛的，即 $\lim\limits_{k\rightarrow \infty}a_k$ 是存在的，则 $\lim\limits_{n\rightarrow \infty}\frac{1}{n}\sum\limits_{k=1}^{\infty}a_k=\lim\limits_{k\rightarrow \infty}a_k$ ，故序列 $\left\{\frac{1}{n}\sum\limits_{k=1}^{n}a_k\right\}_{n=1}^{\infty}$ 是一个收敛序列

其次，证明等价

对于 $E\left[R_{t+1}\vert S_0=s_0\right]$ ，其全期望公式

  • $P^{(t)}(s\vert s_0)$ 表示在第 $t$ 轮迭代中使用的状态转移矩阵因此，起始状态 $s_0$ 并不重要

故有等价成立

最后，对于任意的稳态分布 $d$ ，是否仍然成立

即，对任意的稳态分布 $r(s)$ 都有上述等价形式

5.1.3 策略度量指标的梯度

所有度量指标的梯度有一个统一形式

  • $J(\theta)$ 是不同的策略度量指标 $\overline{V}_{\pi},\overline{r}_{\pi},\overline{V}_{\pi}^0$

  • $=$ 可以是等于、近似、成比例

  • $\eta$ 是状态的分布或状态的权重，在不同问题中呈现不同的分布

    image-20240312104729196

    image-20240312104754749

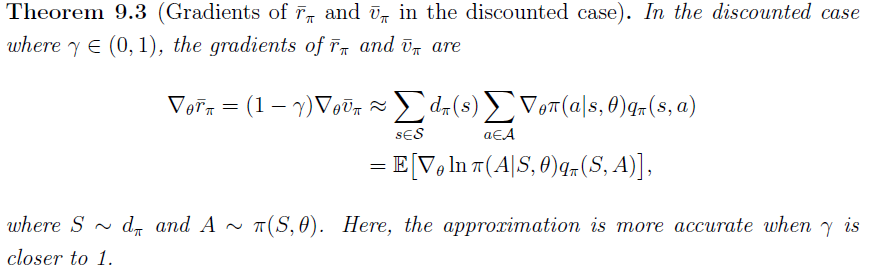
    image-20240312104820120

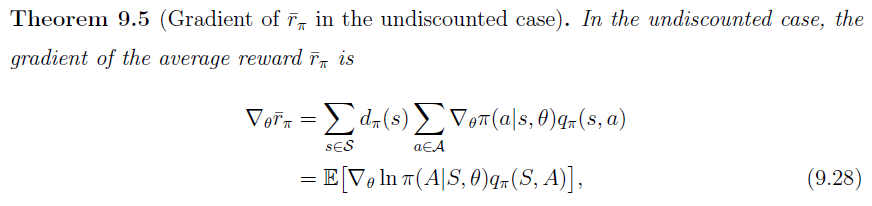
    image-20240312105023700

一些特殊的结果

  • 当折扣情况， $\simeq$ 为 $\approx$ ；当非折扣情况，$\simeq$ 为 $=$

由于 平均单步立即奖励 与 平均状态价值成正比，所以

策略梯度的计算

为了便于计算，需要将梯度改写

将其代入策略度量指标的梯度

此时，目标函数可以用样本近似

注

因为需要计算 $\ln\pi(a\vert s,\theta)$ ，必须保证 $\pi(a\vert s,\theta)>0,\forall a,s,\theta$

在RL中，若不做处理，这个条件并不满足，如贪心策略或确定性策略，有些动作 $\pi(a)=0$

为确保满足条件，需要对所有的 $\pi(a\vert s,\theta)$ 通过 Softmax 函数归一化，将其取值变为 $(0,1)$

Softmax ：对于一个特征向量 $X=\begin{bmatrix}x_1\\\vdots\\x_n\end{bmatrix}$ ，$z_i=\frac{e^{x_i}}{\sum\limits_{j=1}^ne^{x_j}}\in (0,1),\sum\limits_{i=1}^nz_i=1$

决策值可以归一化为

其中，$\pi(a\vert s,\theta)$ 的值由函数 $h(s,a,\theta)$ 确定，即 $h(\cdot)$ 为参数为 $\theta$ 的策略函数，输入状态会给出该状态下执行某个动作的概率

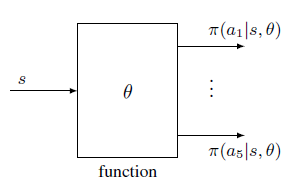
image-20240307164637524

策略函数 $h(\cdot)$ 可以用神经网络实现，输入为 $s$ ，参数为 $\theta$，输出由 $\vert \mathcal{A}(s)\vert$ 个，每个输出对应采取每个动作的概率 $\pi(a\vert s,\theta)$ 且 $\sum\limits_{a\in \mathcal{A}(s)}\pi(a\vert s,\theta)=1$，此时这个神经网络的输出层为 Softmax

  • 由于 $\pi(a\vert s,\theta)>0,\forall a$ ，所以策略是随机性及探索性的
  • 策略梯度也可改为确定性策略

softmax策略的梯度

因此，策略网络的梯度为

5.1.4 与基于价值的学习对比

基于价值的学习由一个 $w$ 为参数的价值函数 $Q(s,a,w)$

优化目标为最小化TD误差：

更新方式

基于策略梯度的学习 由一个 $\theta$ 为参数的策略函数 $\pi(a\vert s,\theta)$

优化目标为最大化策略度量指标

更新方式

5.2 基于蒙特卡洛的策略梯度——REINFORCE

不管采用哪种策略度量指标，对策略函数的优化方法通过梯度上升法最大化 $J(\theta)$

此外，真实的动作价值 $Q_{\pi}(s_t,a_t)$ 也是未知的，需要近似

  • 基于MC方法去近似动作价值，称为 REINFORCE 算法

    用累积奖励值的无偏采样 $Q_{t}(s_t,a_t)=G_t$ 去近似 $Q_{\pi}(s_t,a_t)$

  • 基于TD方法去近似，称为AC算法

5.2.3 伪代码

采样

从 $(s_t,a_t)$ 出发，采集一个回合

  • 采集状态样本： $S\sim d$ ，其中分布 $d$ 状态为在策略 $\pi$ 下的稳态分布

  • 采集动作样本：$A\sim \pi(A\vert S,\theta)$ ，$a_t$ 是策略 $\pi(a\vert s_t,\theta_{t})$ 的采样

由采样也可看出，REINFORCE 算法为同策略 on-policy 算法

REINFORCE是离线方法

基于蒙特卡洛方法，必须将所有的回合数据采集完后才能开始运行，所以策略 $\theta_{t+1}$ 更新后，并没有立即产生数据，即REINFORCE算法是一种离线算法

缺点：

  • 基于片段式数据的任务，任务需要终止状态，才能去计算回报

  • 低数据利用效率：需要大量的训练数据

  • 高训练方差

    从单个或多个片段中采样到的回报去估计动作价值有很高的方差

5.2.2 算法分析

由于 $\bigtriangledown_\theta\ln\pi(a_t\vert s_t,\theta_{t})=\frac{\bigtriangledown_\theta\pi(a_t\vert s_t,\theta_{t})}{\pi(a_t\vert s_t,\theta_{t})}$

其中，$\alpha\beta_t$ 作为梯度上升法的步长，必须足够小

  • 若 $\beta_t>0$ ，则在 $s_t$ 时选择 $a_t$ 的可能性被提高，即 $\pi(a_t\vert s_t,\theta_{t+1})>\pi(a_t\vert s_t,\theta_{t})$ ，且 $\beta_t$ 越大，增大程度越大
  • 若 $\beta_t<0$ ，则 $\pi(a_t\vert s_t,\theta_{t+1})<\pi(a_t\vert s_t,\theta_{t})$

对于任意的$\theta_{t}$ 与 $\theta_{t+1}$ ，当 $\theta_{t+1}-\theta_{t}$ 足够小时，

从微分角度看，随着 $\theta_{t+1}-\theta_{t}\rightarrow 0$ ，这个近似变为等式

其中，梯度上升法步长 $\alpha>0$ ，由此可见，当 $\beta_t>0$ 时，$\pi(a_t\vert s_t,\theta_{t+1})>\pi(a_t\vert s_t,\theta_{t})$ ；当 $\beta_t<0$ ，$\pi(a_t\vert s_t,\theta_{t+1})<pi(a_t\vert s_t,\theta_{t})$

$\beta_t=\frac{Q_{\pi}(s_t,a_t)}{\pi(a_t\vert s_t,\theta_{t})}$ 能很好平衡探索与利用

利用 ：若某个动作价值大， $Q_{\pi}(s_t,a_t)$ 越大，则策略更新后，在 $s_t$ 下选择 $a_t$ 的可能性越大

$\beta_t\propto Q_{\pi}(s_t,a_t)$ ，若 $Q_{\pi}(s_t,a_t)$ 增大，则 $\beta_t$ 会增大，引起 $\pi(a_{t}\vert s_t,\theta_{t+1})$ 增大

探索 ：若在状态 $s_t$ 下，选择动作 $a_t$ 的可能性很小，则策略更新后，会增大选择 $a_t$ 的可能性

$\pi(a_t\vert s_t,\theta_{t})$ 越小，则 $\beta_t$ 越大，从而 $\pi(a_{t}\vert s_t,\theta_{t+1})$ 会增大

5.3 AC方法

将价值近似函数引入到策略梯度中，得到了 Actor-Critic 方法

Actor：策略更新，策略会被应用于决策/动作选择

  • 生成使评论家满意的策略

Critic：策略评估/价值评估，用度量指标衡量策略的优劣

  • 学会准确估计演员策略所采取动作的价值函数
  • QAC
  • A2C：通过引入偏置量减少估计的方差
  • off-policy AC：将on-policy方法转换为 off-policy 方法
    • 重要性采样
  • DPG：随机策略变为确定性策略

策略梯度方法的步骤：

  1. 用于度量策略好坏的策略度量指标函数/目标函数 $J(\theta)$ ，如：$\overline{V}_{\pi},\overline{r}_{\pi}$

  2. Critic（策略评估）：最小化价值函数与价值的损失

  3. Actor（策略更新）

    通过梯度上升法最大化 $J(\theta)$

    为便于计算，使用随机梯度上升法

策略梯度的方法为 Actor ，其中 $Q_t(s_t,a_t)$ 作为价值评估/策略评估，对应 Critic

对于 $\hat{Q}_{w}(s,a)$ 的获取，若使用TD方法，这类算法统称为 AC 方法

5.3.1 QAC

  • 实质上，是 基于价值近似函数的Sarsa+策略梯度

QAC是同策略 on-policy 算法

在求最优化时，由于存在一个期望 $\bigtriangledown_\theta J(\theta_{t})=E_{S\sim \eta,A\sim\pi(A\vert S,\theta)}\left[\bigtriangledown_\theta\ln\pi(A\vert S,\theta)Q_{\pi}(S,A)\right]$ ，故将算法修改为随机梯度上升法

动作需要按照策略 $\pi^{(t)}$ 的分布采样，所以 $\pi^{(t)}$ 是探索策略，同时又是不断改进的策略，所以是目标策略，因此 QAC 是同策略算法

QAC是随机性策略

采取每个动作 $a_t\in \mathcal{A}(s_t)$ 的概率 $\pi(a_t\vert s_t,\theta_{t})>0$

所以，策略本身就具有一定的探索能力 $\pi(a\vert s,\theta)$ ，不需要 $\varepsilon-贪心$ 去探索

5.3.2 A2C

advantage actor-critic(A2C)：核心思想是通过引入一个偏置量 bias 减小方差，即

策略梯度对于额外的偏置量是不变的

额外的偏置量是关于状态变量 $S$ 的偏置量

  • 为什么引入偏置量不改变策略梯度

    相当于证明 $E_{S\sim \eta,A\sim\pi(A\vert S,\theta)}\left[\bigtriangledown_\theta\ln\pi(A\vert S,\theta)b(S)\right]=0$

  • 为什么引入偏置量能减小估计方差

    令 $\bigtriangledown_\theta J(\theta)=E[X]$ ，其中 $X(S,A)=\bigtriangledown_\theta\ln\pi(A\vert S,\theta)\cdot \left(Q_{\pi}(S,A)-b(S)\right)$

    $X$ 的期望 $E[X]$ 与 $b(S)$ 无关，方差 $var(X)$ 与 $b(S)$ 有关

    使用方差的迹评价方差大小，$tr[var(X)]=E[X^TX]-\overline{X}^T\overline{X}$

    已知 $\overline{X}^T\overline{X}=\left(E[X]\right)^TE[X]$ 与偏置量 $b(S)$ 无关

    可见偏置量 $b(S)$ 对策略度量函数梯度的方差有影响，

    为使 $var(X)$ 最小化，最优的偏差应使 $\bigtriangledown_bE[X^TX]=0$ ，即

    且 $b(S)=0$ 不是好的偏置

    • 对于 REINFORCE 与 QAC 算法，其偏置量 $b(S)=0$ ，并不是好的偏置

减小方差的意义：采样时会有更小的误差，在均值相同的情况下，采样时方差小的样本集，每个样本 $X$ 都接近平均值。即使用RM算法近似策略梯度时，随机采集到的每个样本都能接近期望，使策略梯度受随机采样的影响程度最小，进而使得最优化的结果受采样的影响程度最小

因此，在A2C中，算法目标为对 $\theta$ 最优化，使得 $J(\theta)$ 最大，同时，选择一个最优的偏置 $b(S)$ 最小化策略梯度方差 $var(X),X=\bigtriangledown_\theta\ln\pi(A\vert S,\theta)\cdot \left(Q_{\pi}(S,A)-b(S)\right)$

尽管存在最优的偏置量，但为了计算方便，移除权重 $\Vert\bigtriangledown_\theta \ln \pi(A\vert s,\theta_{t})\Vert^2$ ，仅使用次优偏置量

算法

令偏置量 $b(s)=V_{\pi}(s)$

$\delta_\pi(S,A)$ 称为优势函数，因为 $V_{\pi}(s)=\sum\limits_{a\in \mathcal{A}(s)}\pi(a\vert s,\theta_{t})Q_{\pi}(s,a)$ ，即状态价值为动作价值的加权平均，若某个动作价值比均值大，说明这个动作是比较好的，其 $Q(s,a)$ 比均值大，$\delta_{\pi}(s,a)>0$ ，这个动作具有一定优势

  • 使用 $\delta$ 代替动作价值 $Q$ ，因为我们在乎的不是动作价值的绝对大小，而是动作价值间的相对大小

将梯度上升法改为随机梯度上升法

另外，由动作价值定义：

优势函数可以用TD误差来近似：

因此，我们仅需要一个神经网络来近似 $V_{\pi}(S)$ 而不再需要动作价值网络 $Q_{\pi}(S,A)$

伪代码

A2C是同策略算法

在一步迭代后，$\theta_{t}$ 会更新为 $\theta_{t+1}$ ，同时，会基于更新后的策略 $\pi(a\vert s_t,\theta_{t})$ 生成下一步经验，因此策略 $\pi$ 既是目标策略又是探索策略

A2C是随机性策略

由于策略梯度算法需要经过 Softmax 层，所以每个动作的概率 $\pi(a\vert s)>0$ ，即随机性策略

$\mbox{step size}=\frac{\delta_t(s_t,a_t)}{\pi(a_t\vert s_t,\theta_{t})}$ 能很好平衡探索与利用

由于 $\bigtriangledown_\theta\ln\pi(a_t\vert s_t,\theta_{t})=\frac{\bigtriangledown_\theta\pi(a_t\vert s_t,\theta_{t})}{\pi(a_t\vert s_t,\theta_{t})}$

利用

step size 比较大，也就是优势函数 $\hat{\delta}_{t}(s_t,a_t)$ 比较大，即 $a_t$ 的动作价值 $Q_{\pi_{\theta_{t}}}(s_t,a_t)$ 明显大于 $s_t$ 下的平均动作价值 $V_{\pi}(s)$ ，则策略更新后，在 $s_t$ 下选择 $a_t$ 的可能性越大

$\mbox{step size}\propto \hat{\delta}_{t}(s_t,a_t)$ ，若 $\hat{\delta}_{t}(s_t,a_t)$ 增大，则 $\mbox{step size}$ 会增大，策略更新时会朝着 $\pi(a_{t}\vert s_t,\theta_{t+1})$ 增大的方向更新

探索 ：若在状态 $s_t$ 下，选择动作 $a_t$ 的可能性很小，则策略更新后，会增大选择 $a_t$ 的可能性

$\pi(a_t\vert s_t,\theta_{t})$ 越小，则 $\mbox{step size}$ 越大，从而 $\pi(a_{t}\vert s_t,\theta_{t+1})$ 会增大

5.3.3 异策略AC算法

REINFORCE ，QAC ，A2C 都是同策略算法，因为在计算策略度量指标梯度时，涉及到期望的计算

基于RM算法，改为随机梯度下降法，由于在采样过程中，由于动作 $A\sim \pi(A\vert S,\theta_{t})$ 策略 $\pi$ 作为探索策略同时也是目标策略，所以他们都是同策略算法

为复用通过其他方法得到的一些经验，通过 重要性采样 技巧，可将其改为异策略AC算法

  • 同理，重要性采样可用于任何估计期望的算法中

对于异策略算法，我们希望估计 $E_{A\sim \pi}[*],(A\sim p_0)$ ，其中 $\pi$ 是目标策略，而样本基于探索策略 $\mu,(\{a_i\}\sim p_1)$

异策略策略梯度

  1. 策略梯度表达式
  2. 使用梯度上升的方法优化
异策略梯度表达式

设 $\mu$ 为探索策略用于生成经验样本，目标是使用这些经验样本去更新目标策略 $\pi$ ，使得策略度量指标 $J(\theta)$ 最小化

其中，$d_{\mu}$ 是状态 $S$ 在策略 $\mu$ 下的稳态分布

异策略梯度

在折扣奖励情况下 $\gamma\in (0,1)$ ，目标函数 $J(\theta)$ 的梯度为

  • $\mu$ 为探索策略，$\eta$ 为状态服从的分布$Pr_{\pi}(s\vert s’)=\sum\limits_{k=0}^{\infty}\gamma^k\left[P_{\pi}^k\right]_{s’s}=[(I-\gamma P_{\pi})^{-1}]_{s’s}$ ，表示基于策略 $\pi$ 从状态 $s’$ 转移到 $s$ 的概率，其中 $[\cdot]_{s’s}$ 表示矩阵第 $s’$ 行，第 $s$ 列的值
异策略梯度优化

异策略梯度仍引入偏置量 $b(S)$ ，有

为减少估计方差，令偏置量 $b(S)=V_{\pi}(S)$

相应的随机梯度上升算法为

为了便于计算，将优势函数 $\delta_t(s_t,a_t)$ 用TD误差去近似

因此，异策略梯度优化为

充分利用的算法

在异策略梯度中

此时，$\mu(a\vert s_t)$ 可看做是固定值，若 $\hat{\delta}_t(s_t,a_t)$ 越大，则表明动作 $a_t$ 的优势越大，策略更新时要朝着 $a_t$ 增大的方向迭代，即充分利用

伪代码

5.3.4 Deterministic actor-critic(DPG)

策略梯度算法，为便于求解，将策略度量函数的梯度转换为期望形式，使用RM算法去近似估计。而这个转换设计 $\ln \pi$ ，因此，$\pi(a\vert s,\theta)>0,\forall a$ ，即每个动作的概率都不为0，也不会有动作的概率为1，所以 REINFORCE、QAC，A2C，异策略A2C 都是随机性策略

随机性策略的缺点是动作 $a_t$ 的个数必须有限，不能处理连续动作

若改用确定性策略，可以处理连续的动作，表示为 $a=\pi(s,\theta)$ ，相当于采取某个动作的概率为1，其余动作概率为0

  • $\pi$ 为从状态空间 $\mathcal{S}$ 到动作空间 $\mathcal{A}$ 的映射 $\pi:\mathcal{S}\mapsto \mathcal{A}$
  • $\pi$ 也可以是一个神经网络，其输入是状态 $s$ ，输出是一个动作 $a$ ，其参数为 $\theta$

image-20240512000149033

梯度的计算

之前的梯度仅是针对随机策略的梯度，若策略是确定性的，需要重新计算梯度

确定性策略梯度的统一形式

  • $\eta$ 为状态 $s$ 的分布，具体表达式由探索策略下状态的稳态分布与基于策略 $\pi$ 的状态转移确定
  • 对于策略 $\pi$ 下的动作价值 $Q_{\pi}(s,a)$ ，先对 $a$ 求梯度，然后将所有的动作替换为 $\pi(s)$ ——二者是等价的
DPG天然是异策略

首先，actor 是异策略的

  • 求策略度量梯度时并不涉及动作的分布，因为这个动作 $a$ 会被替换为 $\pi(s)$ ，所以不需要 $A$ 对应的分布

    之后使用随机梯度上升法相当于对真实的梯度进行随机采样，若在采样时，给定了一个 $s_t$ ，根据这个状态 $s_t$ 可以得到 $a_t$ ，并不需要关心这个 $a_t$ 是哪个策略得到的，因此可以使用任何的探索策略，即DPG天然是异策略的

其次，critic 也是异策略的

  • 对价值函数的近似需要的经验样本是 $(s_t,a_t,r_{t+1},s_{t+1},\tilde{a}_{t+1})$ ，$\tilde{a}_{t+1}=\pi(s_{t+1})$ ，这个经验样本的生成涉及两个策略

    第一个策略是对状态 $s_t$ 时生成 $a_t$ ，这个策略是探索策略，$a_{t}$ 用于与环境交互

    第二个策略是对状态 $s_{t+1}$ 生成 $\tilde{a}_{t+1}$ ，这个策略必须是 $\pi$ ，因为这是 critic 要去评价的策略 ，所以 $\pi$ 是目标策略，$\tilde{a}_{t+1}$ 在下一时刻并不会用于与环境实际交互

两种常用的度量指标梯度
平均状态价值

将平均状态价值的折扣情况作为策略度量指标

其中，$\sum\limits_{s\in \mathcal{S}}d_0(s)=1$ ，为了便于计算，状态服从与策略 $\pi$ 独立的稳态分布

关于状态分布的选择：

  • $d_0(s_0)=1$ 且 $d_0(s\neq s_0)=0$ ，其中状态 $s_0$ 是我们关注的起始状态

    策略优化的目标是最大化从 $s_0$ 开始的折扣奖励

  • $d_0$ 是另一个不同于 $\pi$ 的探索策略 $\mu$ 下的稳态分布

    与异策略有关，因为DPG算法天然是异策略的，不需要重要性采样进行转换

为计算目标函数的梯度，首先要计算 $\gamma\in (0,1)$ 时 $V_{\pi}(s),\forall s\in \mathcal{S}$ 的梯度

  • 其中，$Pr_{\pi}(s’\vert s)=\sum\limits_{k=0}^{\infty}\gamma^k\left[P^{k}_{\pi}\right]_{ss’}=\left[(I-\gamma P_{\pi})^{-1}\right]_{ss’}$ ，表示基于策略 $\pi$ 从状态 $s$ 转移到 $s’$ 的概率，其中 $[\cdot]_{ss’}$ 表示矩阵第 $s$ 行，第 $s’$ 列的值

策略度量指标的梯度 $\bigtriangledown_\theta J(\theta)$ 为

其中，$\eta_{\pi}(s)=\sum\limits_{s’\in \mathcal{S}}d_0(s’)Pr_{\pi}(s\vert s’)$

  • 其中，$Pr_{\pi}(s\vert s’)=\sum\limits_{k=0}^{\infty}\gamma^k\left[P^{k}_{\pi}\right]_{s’s}=\left[(I-\gamma P_{\pi})^{-1}\right]_{s’s}$ ，表示基于策略 $\pi$ 从状态 $s’$ 转移到 $s$ 的概率，其中 $[\cdot]_{s’s}$ 表示矩阵第 $s’$ 行，第 $s$ 列的值
平均单步立即奖励

将平均单步立即奖励作为策略度量指标

其中，$r_{\pi}(s)=E[R\vert s,a=\pi(s,\theta)]=\sum\limits_{r}rP(r\vert s,a=\pi(s,\theta))$

策略梯度为

  • 其中，$d_{\pi}$ 为状态 $S$ 基于策略 $\pi$ 的稳态分布

DPG算法

基于策略梯度，使用梯度上升法最大化策略度量函数

相应的使用随机梯度上升法去近似

伪代码

对于探索策略 $\mu$ ，也可以将其变为 $\pi+噪音$

每次得到一个 $\pi(s)$ 后，因为 $\pi$ 本身是确定性是，不能探索，所以加上一些噪音，可以有一定的随机性，下一个动作的生成就与目标策略 $\pi$ 有了关系

  • 实质上，$\pi+噪音$ 与 $\varepsilon-贪心$ 非常类似，但这里不能用贪心算法，因为此处应对的时动作空间连续的情况，不能给无限的连续动作赋予一定探索概率

此时，DPG可以变为同策略算法

DPG的进一步改进

使用不同的价值近似基函数去近似 $\hat{Q}(s,a,w)$ 会得到不同的DPG改进算法

  • 线性函数：$\hat{Q}(s_t,a_t,w_{t})=\phi^T(s,a)\cdot w$

    线性近似基函数的难点在于基函数(特征向量)的选择，由于函数结构的限制，逼近动作价值的能力有限

  • 神经网络 ：DDPG

-------------本文结束-------------