矩阵上的运算:特根特向求法,张量积,广义逆
4.1 特根特向求法
4.1.1 特根求法
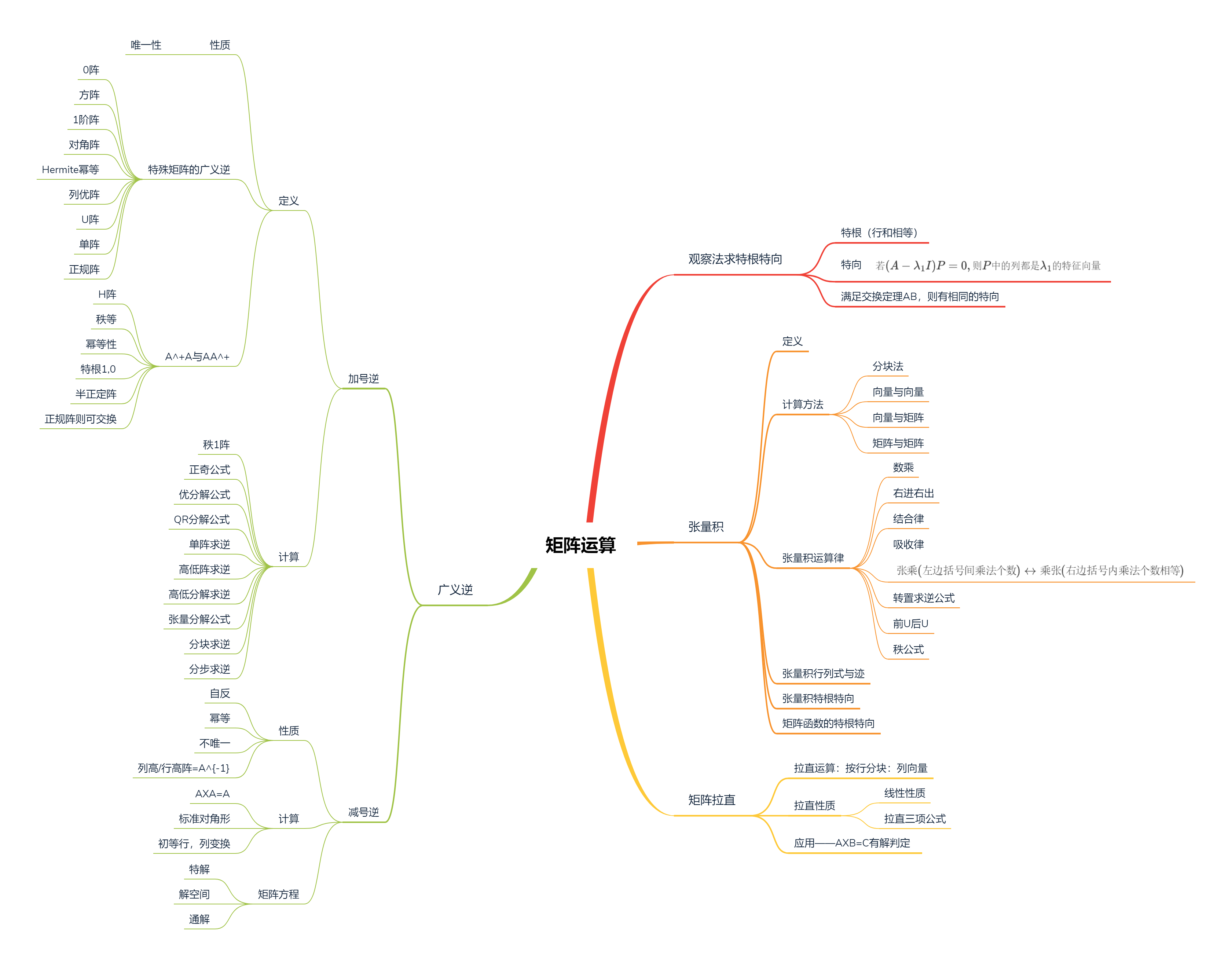
若 $n$ 阶方阵 $A=(a_{ij})$ 中 行和=常数k ,则常数 $k$ 为 $A$ 的一个特征根,全1向量 $X=\left(\begin{matrix}1\\\vdots\\1\end{matrix}\right)$ 为 $k$ 相应的特向
若 $n$ 阶方阵 $A=(a_{ij})$ 中 列和=常数k ,则常数 $k$ 为 $A^T$ 的一个特根,全1向量 $X=\left(\begin{matrix}1\\\vdots\\1\end{matrix}\right)$为 $A^T$ 的一个特向
eg
实对称阵特根为实数
4.1.2 特征向量
证明:
a. 两个互异特根的特向
eg:

b. 三个互异特根的特向
eg
c. 重根的特向
eg

4.1.3 交换定理与公共特征向量
a. Cayley定理
若方阵 $A$ 的特征多项式 $T(x)=\vert A-x I\vert=c_0+c_1x+c_2x^2+\cdots+c_nx^n$ ,则 $T(A)=c_0I+c_1A+c_2A^2+\cdots+c_nA^n=0$
- 方阵A的特征多项式可分解为 $T(x)=(x-\lambda_1)(x-\lambda_2)\cdots(x-\lambda_n)$ 满足 $T(A)=(A-\lambda_1I)(A-\lambda_2I)\cdots(A-\lambda_nI)=0$
b. 交换定理
若方阵 $AB=BA(可交换)$ ,任取 $A$ 的特根 $X$ ,满足 $AX=\lambda_1 X$ , $BX=t_1 X$ ,即 $X$ 是 $A$ 和 $B$ 的公共特征向量
- 若 $A,B$ 可交换,则存在公共特向 $X\neq 0$
证明:
c. 可交换的实对称阵为单阵
若 $A,B$ 为 $n$ 阶实对称阵,且可交换 $AB=BA$ ,则存在正交阵 $Q$ ,使 $Q^{-1}AQ,Q^{-1}BQ$ 为对角阵
4.2 张量积
4.2.1 定义
设 $A=(a_{ij})_{m\times n}$ ,$B=(b_{ij})_{p\times q}$ ,则称分块矩阵 $\left(\begin{matrix}a_{11}B&a_{12}B&\cdots&a_{1n}B\\a_{21}B&a_{22}B&\cdots&a_{2n}B\\\vdots&\vdots&\ddots&\vdots\\a_{n1}B&a_{n2}&\cdots&a_{nn}\end{matrix}\right)$ 为 $A$ 与 $B$ 的张量积,记作 $A\otimes B=(a_{ij}B)_{mp\times nq}$
eg
- 张量积不满足交换律 ,即 $A\otimes B\neq B\otimes A$
定理
两个上三角的张量积也是上三角
两个对角阵的张量积是对角阵
$I_n\otimes I_m=I_{m}\otimes I_n=I_{m\times n}$
4.2.2 计算
a. 分块法
右进右出
一般情况下:$F \otimes (A\quad B)\neq (F\otimes A\quad F\otimes B)$

b. 向量与向量张量积
c. 向量与矩阵张量积
4.2.3 运算律
数乘: $k(A\otimes B)=(kA)\otimes B=A\otimes (kB)$
分配律(右进右出):$(A+B)\otimes C=A\otimes C+B\otimes C$ ,$C\otimes(A+B)=C\otimes A+C\otimes B$
结合律:$(A\otimes B)\otimes C=A\otimes (B\otimes C)$
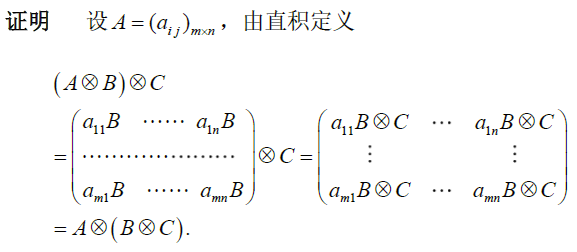
吸收律:$(A\otimes B)(C\otimes D)=(AC)\otimes (BD)$
$张乘(左边括号间乘法个数)\leftrightarrow 乘张(右边括号内乘法个数相等)$
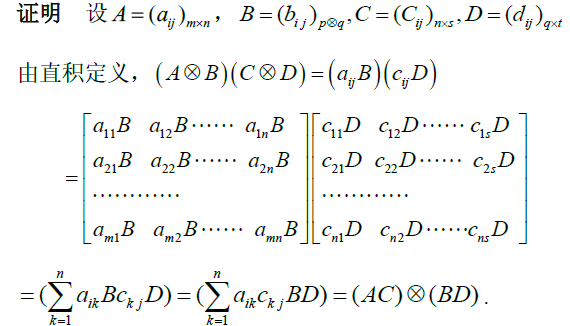
推论:
eg:
- 转置与求逆公式:
若A与B都是U阵,则 $A\otimes B$ 为U阵
秩公式:$r(A\otimes B)=r(A)r(B)$
推论:
由于 $r(\{X\otimes Y\})=r(\{X\})r(\{Y\})$ ,张量积的秩等于两个向量组的秩的乘积,所以张量积线性无关
4.2.4 张量积行列式
设 $A=(a_{ij}) \in C^{m\times m} ,B=(b_{ij})\in C^{n\times n}$ ,则
证明:
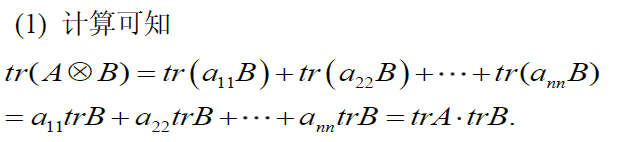
4.2.5 张量积特征值特征向量
a. 特征值
若 $A=A_{m\times m}$ 的特征根为 $\lambda_1,\lambda_2,\cdots,\lambda_m,B=B_{n\times n}$ 的特征根为 $t_1,t_2,\cdots,t_n$
$A\otimes B$ 的全体特征根为 $mn$ 个数 $\{\lambda_it_j\}$ ,有重根
$A\otimes I_n\pm I_m\otimes B$ 是的全体特根为 $mn$ 个数 $\{\lambda_i\pm t_j\}$
b. 特征向量
设 $\{X_1,\cdots,X_p\}$ 是 $A\in C^{m\times m}$ 关于 $\lambda$ 的线性无关的特征向量, $\{Y_1,\cdots,Y_q\}$ 是 $B\in C^{n\times n}$ 关于t的线性无关的特征向量
- $pq$ 个向量 $\{X_i\otimes Y_j\}$ 是 $A\otimes B$ 关于 $\lambda t$ 的特征向量
- $\{X\otimes Y\}$ 是 $A\otimes I_n\pm I_m\otimes B$ 关于 $\lambda+t$ 的一个特征向量

eg

c. 矩阵函数的特根特向
设 A 和 B 分别是 m 阶与 n 阶方阵, $f(x,y)$ 是二元多项式, $f(x,y)=\sum_{i,j=1}\limits^pc_{ij}x^iy^j$
定义 mn 阶矩阵 $f(A,B)$ 如下:

4.3 矩阵拉直
4.3.1 定义
按行拉直:设矩阵 $A=(a_{ij})_{m\times n}$ ,其按行拉直向量为一个列向量 $\vec{A}=\left(a_{11},\cdots,a_{1n},\cdots,a_{m1},\cdots,a_{mn}\right)^T$
引理:设 $A=(a_{ij})_{m\times n}$ ,记 $A$ 的 $m$ 个行分块为 $A_1,\cdots,A_m$ ,则有 $A=\left(\begin{matrix}A_1\\\vdots\\A_m\end{matrix}\right)$ ,则 $\vec{A}=\left(\begin{matrix}A_1^T\\\vdots\\A_m^T\end{matrix}\right)$
按行拉直:按行分块,列向量
eg
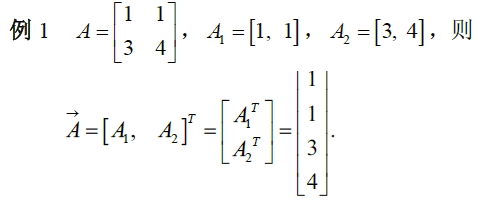
4.3.2 拉直性质
线性性质:
- $\overrightarrow{A+B}=\vec{A}+\vec{B}$
- $\overrightarrow{kA}=k\vec{A}$
$X=X(t)\in C^{m\times n}$ ,则 $\frac{\overrightarrow{dX}}{dt}=\frac{d}{dt}\vec{X}$
拉直三项公式
$\overrightarrow{ABC}=(A\otimes C^T)\vec{B}$

在方程组中为 $\overrightarrow{AXB}=(A\otimes B^T)\vec{X}$
乘积推广:两项拉直可以看做特殊三项拉直
设 $A=(a_{ij})_{m\times m},X=(x_{ij})_{m\times n},B=(b_{ij})_{n\times n}$
4.3.3 应用——矩阵方程AXB=C有解判定
见:6.2 矩阵方程求解
4.4 加号逆
4.4.1 定义
若 $m\times n$ 矩阵 $A=A_{m\times n}$ 与矩阵 $X=X_{n\times m}$ 满足四个条件
- $AXA=A$
- $XAX=X$
- $(AX)^H=AX$
- $(XA)^H=XA$
则 $X$ 为 $A$ 的加号逆(广义逆),记为 $X=A^+$
a. 性质
$A$ 与 $A^+$ 互为加号逆
$A^{+}$ 具有唯一性
$A^+$ 的H穿脱公式:$(A^H)^+=(A^+)^H$
乘积的加号逆无穿脱公式:$(AB)^+\neq B^+A^+$
b. 特殊矩阵的加号逆
$A=0$ ,则 $A^{+}=0$
若方阵 $A=A_{n\times n}$ 可逆 ($\vert A \vert\neq 0$) ,则 $A^+=A^{-1}$
若 $A=(a)$ 为1阶阵,即 $A=(复数a)$ ,则有 $(a)^+=a^+=\left\{\begin{aligned}a^{-1},&a\neq 0\\0,&a=0\end{aligned}\right.$
对角阵 $D=\left(\begin{matrix}a_1&&&\\&a_2&&\\&&\ddots\\&&&a_n\end{matrix}\right)$ ,则 $D^+=\left(\begin{matrix}a_1^+&&&\\&a_2^+&&\\&&\ddots\\&&&a_n^+\end{matrix}\right)$
eg:
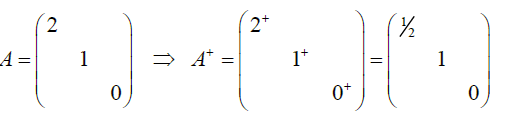
$D^+D=DD^+$ ,且 $(D^+)^k=(D^k)^+$ ,(k=1,2,…)
证明:

A为Hermite幂等阵,即 $A^H=A=A^2$ ,则 $A^+=A=A^H$
若A为列优阵($A^HA=I$) ,则 $A^+=A^H$
若 $A^H$ 为列优阵(A为行优阵)($AA^H=I$) ,则 $A^+=A^H$
若A为U阵(
单位正交阵),则 $A^+=A^H=A^{-1}$若A为U阵,则 $A^HA=AA^H=I,A^H=A^{-1}$
$A^HAA^H=A^H,AA^HA=A,(AA^H)^H=I=AA^H,(A^HA)^H=A^HA$ ,故 $A^+=A^H$
若A为单阵(
可相似对角化)且可逆 ,则有谱分解 $A=\lambda_1G_1+\cdots+\lambda_kG_k$ 且 $A^+=\lambda_1^{-1}G_1+\cdots+\lambda_k^{-1}G_k$若不满足可逆条件,则未必成立
若A为正规阵(
正规方阵),则 $A^+$ 也为正规阵有正规分解 $A=QDQ^H$ ,则 $A^+=QD^+Q^H$
有谱分解 $A=\lambda_1^+G_1+\cdots+\lambda_k^+G_k$
c. $AA^+$ 与 $A^+A$ 相关结论
$AA^+$ 与 $A^+A$ 都是Hermite阵
幂等性
$(A^+A)^2=A^+A,(AA^+)^2=AA^+$
$(I-A^+A)^2=I-A^+A$
$r(I-A^+A)=n-r(A^+A)=n-r(A)$
$r(I-AA^+)=r(A)$
$r(A^+A)=r(AA^+)=r(A)=tr(AA^+)=tr(A^+A)$
由于矩阵的秩越乘越小,则 $r(AA^+)\le r(A)$ 而 $A=AA^+A$ ,则 $r(A)\le r(AA^+)$ ,故有 $r(AA^+)\le r(A)\le r(AA^+)$
幂等性:$(AA^+)^2=AA^+$ ,$(A^+A)^2=A^+A$
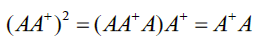
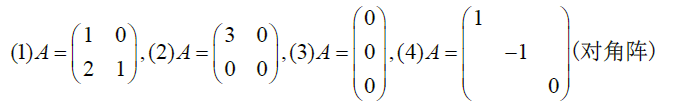
$\lambda(AA^+)$ 与 $\lambda(A^+A)$ 都有 $r(A)$ 个1
设 $A\in C^{m,n},A^+\in C^{n,m}$ 由于 $AA^+$ 与 $A^+A$ 都是 Hermite 阵,且 $A^+A$ 是幂等阵, $(AA^+)^2=AA^+,(A^+A)^2=A^+A$ ,由Cayley定理 $x^2=x$ 则其0化式为 $x^2-x=0$ ,$AA^+$ 有两个不同的根1和0
已知 $r(A^+A)=r(AA^+)=r(A)=r$ ,
则 $AA^+$ 有r个正根,m-r 个0根;$A^+A$ 有r个正根,n-r 个0根
$A^+A$ 与 $AA^+$ 都是半正定阵 ($AA^+ \ge 0,A^+A\ge 0$)
已知 $A^+A$ 为幂等阵,则 $(AA^+)^2=(AA^+)^H(AA^+)\xlongequal{P=AA^+}P^HP\ge 0$ ,故 $AA^+$ 为半正定阵,同理 $AA+$ 为半正定阵
由Cayley定理,$x^2=x$ ,则0化式 $x(x-1)=0$ ,故特根 $\ge$ 0 ,为半正定阵
一般有 $AA^+\neq I$ , $A^+A\neq I$ (列半U以上), 且 $AA^+\neq A^+A$ (正规阵)
若 A 为正规阵,则 $A^+A=AA^+$ ,且 $(A^+)^k=(A^k)^+,k=0,1,2,\cdots$
4.4.2 $A^+$ 计算
a. 秩1阵
$A^HA$ 的相关结论:
- $tr(A^HA)=t(AA^H)=\sum\vert a_{ij}\vert^2=\Vert A \Vert_F^2$
- $r(A^HA)=r(AA^H)=r(A)$
- $A^HA,AA^H$ 为半正定阵
证明:
eg:

b. 正奇分解求逆(第一公式)
由 $A^+$ 的正奇公式,可证 逆的H穿脱公式 $(A^H)^+=(A^+)^H$
- $A^+$ 的正奇值为 $\{s_1^{-1},s_2^{-1},\cdots,s_r^{-1}\}$ ,且有公式 $\Vert A^+\Vert_F=\sqrt{s_1^{-2},\cdots,s_r^{-2}}$ ,$\Vert A^+\Vert_2=s_r^{-1}$
证明:
eg
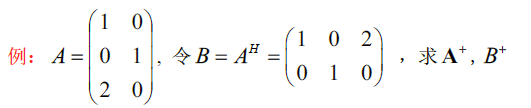
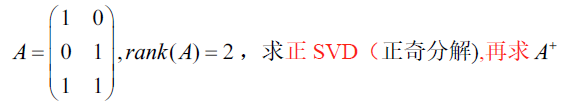
c. 优分解求逆公式
- 引理:若 $D=\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)$ 为对角阵,则 $D^+D=DD^+$ ,且 $(D^+)^k=(D^k)^+$ ,(k=1,2,…)
d. QR分解求逆公式
eg
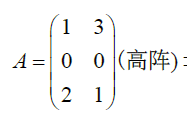
e. 单阵求逆
若A为单阵不可逆,则不能用谱分解方式求逆
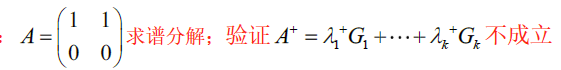
若A为单阵且可逆,则有谱分解 $A=\lambda_1G_1+\cdots+\lambda_kG_k$ 且 $A^+=\lambda_1^{-1}G_1+\cdots+\lambda_k^{-1}G_k$

正规阵谱分解
eg
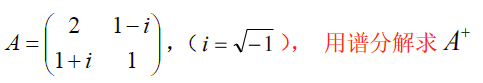
f. 高低阵求逆及高低分解求逆公式
引理
高低阵引理:

高低阵消去性质:

Hermite性质:


高低阵求逆
eg
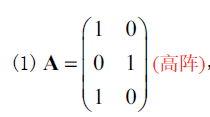
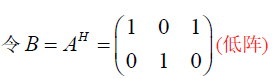
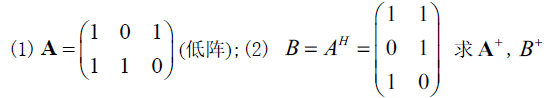
$A^+$ 第二公式(高低分解求逆公式)
注
$(BC)^+$ 一般不成立,只有在高低分解时才成立
eg
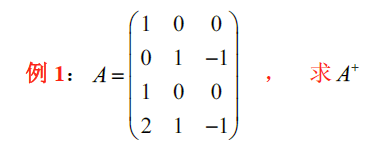
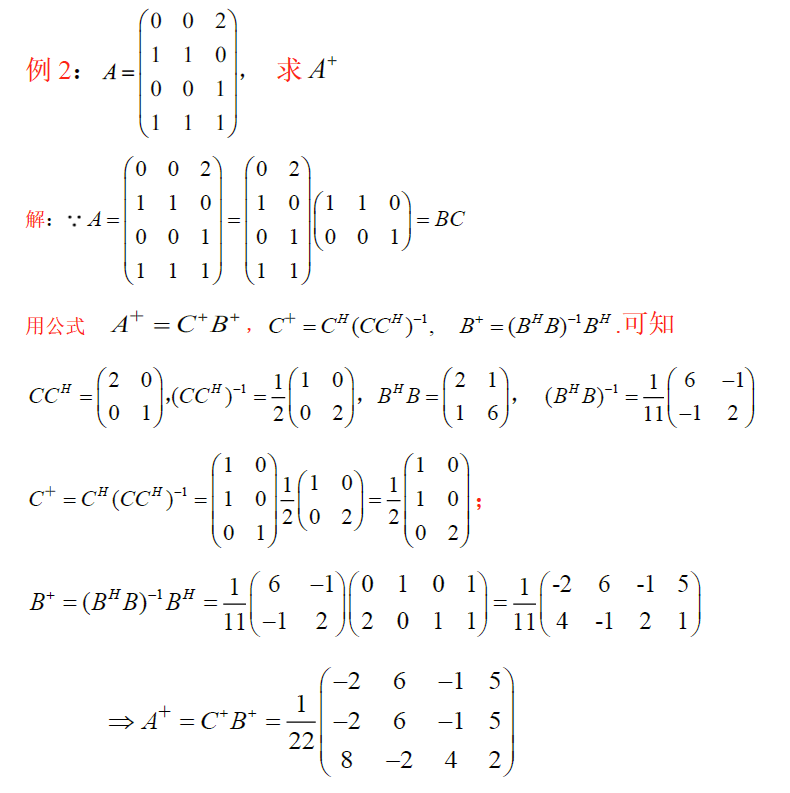
g. 张量分解公式

h. 分块求逆公式
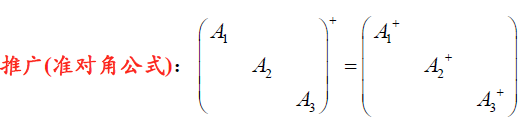
eg

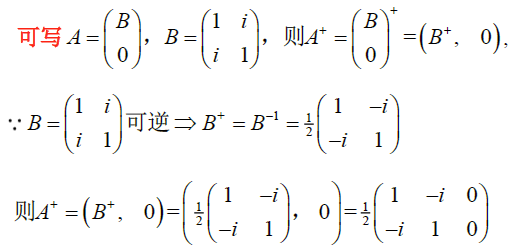


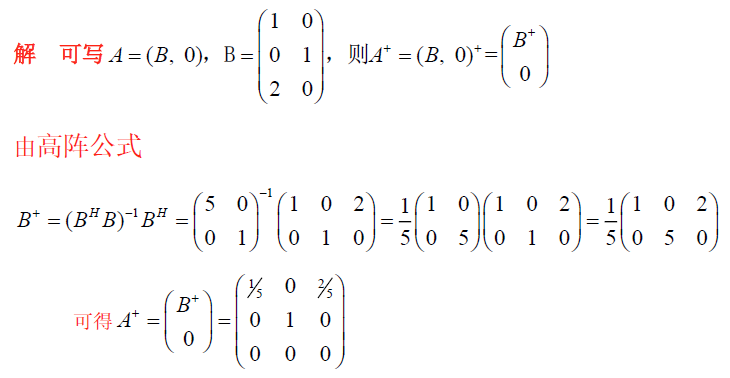
eg

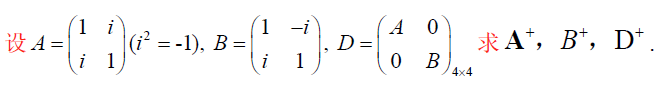
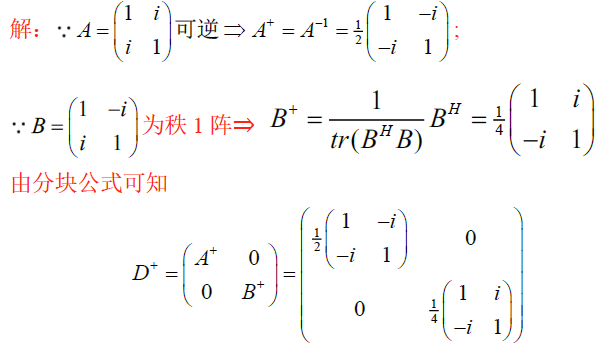
i. 第三公式(分步求逆)

应用

eg

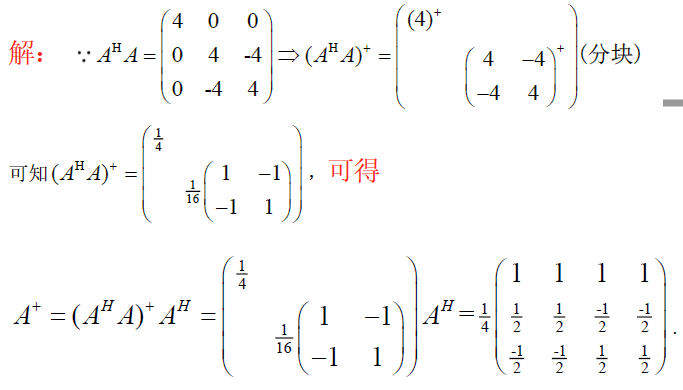
4.5 减号逆
若 $A=A_{m\times n}$ 与 $X=X_{n\times m}$ ,有 $AXA=A$ ,则称 $X=X_{n\times m}$ 为A的减号逆(一号逆),记为 $X=A^{-}=A^{(1)}$
全体 $A^{-}$ 的集合记为 $A^{\{1\}}=\{X\mid AXA=A\}$
- $A^{-}\in A^{\{1\}}$
4.5.1 性质
a. 自反性
$AA^{-}A=A$
b. $A^-A$ 为幂等阵
$(A^{-}A)^2=A^{-}A$ , $(AA^{-})^2=AA^{-}$
秩迹公式
$r(A)=r(A^-A)=r(AA^-)=tr(AA^-)=tr(A^-A)$
$(I-A^-A)^2=I-A^-A$
- $r(I-A^-A)=n-r(A^-A)=n-r(A)$
- $r(I-AA^-)=r(A)$
c. $A^{-}$ 不唯一
- 如 $A=\left(\begin{matrix}1\\0\end{matrix}\right)$ ,可取 X=(1 0) 或 Y=(1 1) 作为A的减号逆
- $A^{-}$ 唯一的阵:方阵$A_{n\times n}$可逆,则必有唯一 $A^{-1}=A^{+}=A^-$
d. 满秩乘积为单位阵
若 $A=A_{m\times n}$ 为列满秩(高阵),则 $A^-A=I_n$ ;若 $A$ 为行满秩(低阵),则 $AA^-=I_m$

4.5.2 计算
a. 求解$AXA=A$
求解减号逆 $A{-}$ 即求解 $AXA=A$ 的全体通解
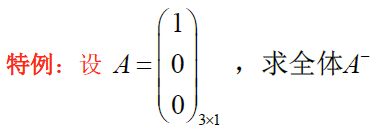
也可见 $A^-$ 不唯一
- 对于高阶阵 $A^-=A^++(Y-A^+AYAA^+)$ 的计算比较复杂
b. 标准对角形
若 $A=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}$ ,则全体 $A^-=\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}$ ,BCD为任一小块

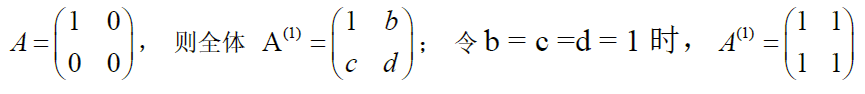
SP
若 $PAQ=\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}$ ,全体 $A^{-}=Q\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}P$ ,BCD为任一小块
c. 初等行,列变换(一般方法)
设 $A=A_{m\times n}$ ,令 $\left(\begin{array}{c:c}A&I_m\\\hdashline I_n&0\end{array}\right)\xrightarrow[列变换]{行变换}\left(\begin{array}{c:c}\left(\begin{matrix}I_r&0\\0&0\end{matrix}\right)_{m\times n}&P\\\hdashline Q&0\end{array}\right)$ ,则有 $A^-=Q\left(\begin{matrix}I_r&B\\C&D\end{matrix}\right)_{n\times m}P$
eg

4.5.3 矩阵方程求解
前置知识:正规方程求解
a. 特解

b. 解空间
$N(A)$ 或 $AY=0$ 的通解为 $Y=(I_n-A^-A)y$ ,$\forall y\in C^n$
$N(A)=\{Y\vert AY=0\}$ ,$X=(I_n-A^-A)y,y=\left(\begin{matrix}y_1\\\vdots\\y_n\end{matrix}\right)\in C^n$
设y的值域为 R,则 $N(A)=R(I_n-A^-A)$ ,维数 $dim N(A)=n-r(A^-A)$
c. 通解

