[TOC]

5. 深度计算

5.1 层和块

5.1.1 块的概念

整个深度模型包含一些参数（所有组成层的参数集合），接受原始输入，生成输出。同样，每个层包含该层的参数，接受上一层提供的输出作为输入，并生成该层输出，这些参数根据下一层反向传播的信息被更新（误差反向传播）

视觉领域，ResNet-152有数百层，这些层由层组(groups of layers) 堆叠组成
其他领域，也有层组堆叠排列的类似架构

因此将神经网络组成模块划分为块（Module），块可描述单个层、多个层组成的层组或深度模型本身。

5.1.2 pytorc中的块

从编程实现角度，块的概念就是类。块 nn.Module 的任何子类都必须定义 $输入\mapsto 输出$ 的前向传播函数 forward(self,X) ；对各层输入、输出参数的初始化（该层参数形状）

反向传播函数用于计算梯度，但由于自动微分的引入，不需要考虑

import torch
from torch import nn
# functional 库封装常用函数库
from torch.nn import functional as F

# 重点是这部分的理解
net = nn.Sequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))

X = torch.rand(2, 20)
net(X)
#	tensor([[ 0.0343,  0.0264,  0.2505, -0.0243,  0.0945,  
#	         0.0012, -0.0141,  0.0666,-0.0547, -0.0667],
#	        [ 0.0772, -0.0274,  0.2638, -0.0191,  0.0394, 
#	         -0.0324,  0.0102,  0.0707,-0.1481, -0.1031]], 
#	       grad_fn=<AddmmBackward0>)

nn.Sequential 构建了一个深度模型，层的顺序是参数传入的顺序

nn.Sequential ：是 nn.Module 的一个子类，维护块实例的有序列表（也是 nn.Module 的实例 / 子类实例）

1 2	>>> print(nn.Sequential.__mro__) (<class 'torch.nn.modules.container.Sequential'>, <class 'torch.nn.modules.module.Module'>, <class 'object'>)

net(参数) 调用深度模型：相当于 net.__call__(X) 的简写

自定义块

块提供的功能

存储和访问前向传播计算所需的参数
根据需要初始化模型参数
接收输入数据：作为前向传播函数的参数
通过前向传播函数生成输出
计算输出关于输入的梯度：反向传播函数访问；通常自动微分完成

class MLP(nn.Module):
    # 用模型参数声明层
    def __init__(self):
        # 调用MLP的父类Module的构造函数来执行必要的初始化。
        # 	子类实例化时也可以指定其他函数参数，例如模型参数params
        super().__init__()
        # 实例化两个全连接层
        self.hidden = nn.Linear(20, 256)  # 隐藏层
        self.out = nn.Linear(256, 10)  # 输出层

    # 定义模型的前向传播，即如何根据输入X返回所需的模型输出
    #	以X作为输入， 计算带有激活函数的隐藏表示，并输出其未规范化的输出值
    def forward(self, X):
        # 注意，这里我们使用ReLU的函数版本，其在nn.functional模块中定义。
        return self.out(F.relu(self.hidden(X)))
    
net = MLP()
net(X)
#	tensor([[ 0.0669,  0.2202, -0.0912, -0.0064,  0.1474, 
#	         -0.0577, -0.3006,  0.1256,-0.0280,  0.4040],
#	        [ 0.0545,  0.2591, -0.0297,  0.1141,  0.1887,
#	         0.0094, -0.2686,  0.0732,-0.0135,  0.3865]], 
#	       grad_fn=<AddmmBackward0>)

顺序块

Sequential的设计是为了把其他模块串起来

__init(self, *args)__ ：将块逐个追加到列表中
forward ：前向传播：将输入按追加块的顺序前向传播

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for idx, module in enumerate(args):
            # 这里，module是Module子类的一个实例。
            # _modules：保存module实例的有序字典实例；属于 OrderedDict 类
            self._modules[str(idx)] = module

    def forward(self, X):
        # OrderedDict保证了按照成员添加的顺序遍历它们
        for block in self._modules.values():
            # X是经过运算块后的返回值，相当于各层的输出
            X = block(X)
        # 这里返回的前向输出
        return X

自定义有序字典类 OrderedDict 作用：在模型初始化过程中，pytorch从其实例 _modules 中查找需要初始化参数的子块

net = MySequential(nn.Linear(20, 256), nn.ReLU(), nn.Linear(256, 10))
net(X)
#	tensor([[ 2.2759e-01, -4.7003e-02,  4.2846e-01, -1.2546e-01,  1.5296e-01,
#			1.8972e-01,  9.7048e-02,  4.5479e-04, 	-3.7986e-02,  6.4842e-02],
#	        [ 2.7825e-01, -9.7517e-02,  4.8541e-01, -2.4519e-01, -8.4580e-02,
#			2.8538e-01,  3.6861e-02,  2.9411e-02, 	-1.0612e-01,  1.2620e-01]], grad_fn=<AddmmBackward0>)

nn.ReLU() 内部调用了 F.rele() ，具有状态和可学习参数

块访问

nn.Sequential 实例可以理解为一个 nn.module 类实例的有序列表，可以通过索引来访问模型的任一层

# 访问顺序块，返回顺序块实例信息
print(net)
# MySequential(
#   (0): Linear(in_features=20, out_features=256, bias=True)
#   (1): ReLU()
#   (2): Linear(in_features=256, out_features=10, bias=True)
# )

# 返回OrderedDict类实例，封装了该顺序块关联的块字典列表
print(net._modules)
# OrderedDict([('0', Linear(in_features=20, out_features=256, bias=True)), 
#				('1', ReLU()), 
#				('2', Linear(in_features=256, out_features=10, bias=True))])

# 根据索引获取字典中的块实例
print(net[2])#nn.Sequential中实现了通过索引访问，与下列两种方式等价
print(net._modules['2'])
print(net._modules.get('2'))
#	Linear类继承Module类
#			Linear(in_features=256, out_features=10, bias=True)

自定义块的特殊用法

Sequential 类允许我们定制深度网络架构，并提供很大灵活性。如：可以在前向传播中引入控制流或自定义处理

层引入常数参数

若在某一层需要合并一些其他参数 常数参数(constant param) ：既不是上一层结果也不是可更新参数，如 $f(\mathbf{x};\mathbf{W})=c\mathbf{x}\mathbf{W}^T$ ，$c$ 就是常数参数，整个优化过程没有被更新

class FixedHiddenMLP(nn.Module):
    def __init__(self):
        super().__init__()
        # 不计算梯度的随机权重参数。因此其在训练期间保持不变
        self.rand_weight = torch.rand((20, 20), requires_grad=False)
        self.linear = nn.Linear(20, 20)
	
    # 1.计算线性层输出
    # 2.对第一次输出乘常量参数+1，再relu
    # 3.计算第二次输出的线性层输出
    # 4.控制流：若X每个元素绝对值的和>1，则除2直至小于1
    # 5.返回标量，X.sum()
    def forward(self, X):
        X = self.linear(X)
        # 使用创建的常量参数以及relu和mm函数
        X = F.relu(torch.mm(X, self.rand_weight) + 1)
        # 复用全连接层。这相当于两个全连接层共享参数
        X = self.linear(X)
        # 控制流
        while X.abs().sum() > 1:
            X /= 2
        return X.sum()

块组合

Sequential 类允许我们定制深度网络架构，并提供很大灵活性

class NestMLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(20, 64), nn.ReLU(),
                                 nn.Linear(64, 32), nn.ReLU())
        self.linear = nn.Linear(32, 16)

    def forward(self, X):
        return self.linear(self.net(X))

chimera = nn.Sequential(NestMLP(), nn.Linear(16, 20), FixedHiddenMLP())
chimera(X)

5.1.3 操作效率

在一个高性能的深度学习库中进行了大量的字典查找、代码执行和许多其他的Python代码。 Python的问题全局解释器锁是众所周知的。在深度学习环境中，我们担心速度极快的GPU可能要等到CPU运行Python代码后才能运行另一个作业。

5.2 参数管理

Paramater 类的实例是可优化的参数实例

在定义好模型架构并设置好超参数后，完成对 各层参数设置 后，就可以进行模型训练

访问参数
参数初始化
不同 块(module) 间共享参数

import torch
from torch import nn

net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
# 2个数据4维特征
X = torch.rand(size=(2, 4))
net(X)

5.2.1 参数访问

net.state_dict() 返回块的所有参数信息组成的字典 OrderedDict

权重就是神经网络的状态，权重的一轮迭代就是网络状态的一次变化

# 使用nn.Sequential，该类封装了一些按索引访问方法，支持列表式访问各层
print(net[2])
# net[2] 返回Linear类的块实例，即本层信息
#	Linear(in_features=8, out_features=1, bias=True)

# Module有state_dict()：返回 a dictionary containing a whole state of the module
print(net.state_dict())
#OrderedDict([
#    ('0.weight', tensor([[-0.3076, -0.4758,  0.1081, -0.2304],
#        [ 0.4211,  0.4465, -0.3960, -0.1722],
#        [ 0.2387,  0.3205,  0.2718,  0.2265],
#        [ 0.2729,  0.1801, -0.1720, -0.0440],
#        [-0.1461, -0.1271,  0.1468,  0.3713],
#        [-0.4266,  0.4993,  0.1876, -0.3648],
#        [-0.3004,  0.0743, -0.3056,  0.0593],
#        [ 0.0245, -0.1389, -0.1488, -0.4814]])), 
#    ('0.bias', tensor([-0.2036, -0.0883,  0.4036, -0.3335, -0.4430,  0.2864, -0.1805, -0.1634])), 
#    ('2.weight', tensor([[ 0.2721,  0.2518,  0.3448,  0.2209,  0.1964, -0.1971,  0.0200,  0.2595]])), 
#    ('2.bias', tensor([0.1401]))])

net.state_dict()['0.bias']
# tensor([-0.0771, -0.1678, -0.3164, -0.3792,  0.1848, -0.2182,  0.3182, -0.1454])

# Linear类继承了Module类
print(net[2].state_dict())
# 	OrderedDict([('weight', tensor([[-0.2372, -0.2587, -0.2270, -0.1828, -0.1542, -0.2847,  0.1730, -0.1300]])), ('bias', tensor([-0.1647]))])

Linear类实例的输出是一个字典，键包括：权重，偏置

键唯一标识每个参数

参数类

每个参数都被表示为一个参数类实例（<class 'torch.nn.parameter.Parameter'>），属性有：

值：data
梯度：grad
其他额外信息

这些参数信息可以被统一管理和更新，所以需要 Parameter 类

print(type(net[2].bias))
# <class 'torch.nn.parameter.Parameter'>

# 返回的是参数类实例 参数名为bias的实例
print(net[2].bias)
# 	Parameter containing:
# 	tensor([-0.1647], requires_grad=True)

# 只返回bias属性的值
print(net[2].bias.data)
#	tensor([-0.1647])
print(net[2].bias.grad)

一次性访问所有参数`net.named_parameters()`

# *[...]参数解包
#	接收元组的list，并将其作为两个单独的参数分别输出
print(*[(name, param.shape) for name, param in net[0].named_parameters()])
#('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
# param是Parameter类的实例

print(*[(name, param.shape) for name, param in net.named_parameters()])
#('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight',torch.Size([1, 8])) ('2.bias', torch.Size([1]))

从嵌套块收集参数

深度模型中，层之间存在嵌套关系，也可以通过嵌套列表索引分层访问块参数

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                         nn.Linear(8, 4), nn.ReLU())

def block2():
    net = nn.Sequential()
    for i in range(4):
        # f'{i}' 格式化字符串，将{i}中的变量值替换
        net.add_module(f'block {i}', block1())
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

print(rgnet)

# rgnet[0]=block2()
# rgnet[0][1]=block2()[1]=(block 1)
# rgnet[0][1][0]=block2()[1][0]=(block 1)[0]=Linear(in_features=4,out_feartures=8,bias=True)
# rgnet[0][1][0].bias=tensor(8)
rgnet[0][1][0].bias.data

5.2.2 参数初始化

pytorch提供默认随机初始化，也允许通过重写自定义初始化方法

默认情况下，PyTorch会根据一个范围均匀地初始化权重和偏置矩阵，这个范围是根据输入和输出维度计算出的——Xavier初始化

预置初始化

nn.init 模块提供类很多预置的初始化方法

正态分布
全0，全1
常量
Xavier初始化

正态分布、全0/全1

def init_normal(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, mean=0, std=0.01)
        nn.init.zeros_(m.bias)
        
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0]

net.apply(fn) 递归地将一个函数应用到神经网络中的每个子模块上，包括其本身

需要定义一个函数，该函数接收一个模块作为参数，并对该模块执行自定义操作

常量

def init_constant(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 1)
        nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0]
# (tensor([1., 1., 1., 1.]), tensor(0.))

Xavier初始化

xavier_normal
xavier_normal_ ：这个是更新后的版本，在计算时会考虑到ReLU激活函数的特性，以确保网络在初始化时的激活值分布更加合理
xavier_uniform
xavier_uniform_

def init_xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
def init_42(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)

自定义初始化

$\begin{aligned} w \sim \begin{cases} U(5, 10) & \text{ 可能性 } \frac{1}{4} \\ 0 & \text{ 可能性 } \frac{1}{2} \\ U(-10, -5) & \text{ 可能性 } \frac{1}{4} \end{cases} \end{aligned}$

def my_init(m):
    if type(m) == nn.Linear:
        print("Init", *[(name, param.shape)
                        for name, param in m.named_parameters()][0])
        nn.init.uniform_(m.weight, -10, 10)
        m.weight.data *= m.weight.data.abs() >= 5

net.apply(my_init)
net[0].weight[:2]

也可以在任意位置直接修改参数

net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42

net[0].weight.data[0]
# tensor([42.0000, -5.2469,  9.0045,  1.0000])

5.2.3 参数共享

在层之间共享权重，实质上共享层引用是同一个参数矩阵的值

# 我们需要给共享层一个名称，以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象，而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])
# tensor([True, True, True, True, True, True, True, True])
# tensor([True, True, True, True, True, True, True, True])

net有4个隐藏层，第二个隐藏层和第三个隐藏层都由shared定义

作用：由于模型参数包含梯度，因此在反向传播期间参数共享层的梯度会加在一起

5.3 自定义层

与自定义块类似，只需要继承 nn.module ，并实现 __init__(self) 和 forward(self,X) 即可

5.3.1 不带参数的层

import torch
import torch.nn.functional as F
from torch import nn

class CenteredLayer(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, X):
        return X - X.mean()
    
layer = CenteredLayer()
# 将数据 X=[1,2,3,4,5] 传入该层，会输出前向传播的值
layer(torch.FloatTensor([1, 2, 3, 4, 5]))
#	tensor([-2., -1.,  0.,  1.,  2.])

只要继承了 nn.Module 类的块都可以应用到更复杂的模型中

net = nn.Sequential(nn.Linear(8, 128), CenteredLayer())

Y = net(torch.rand(4, 8))
Y.mean()
#	tensor(7.4506e-09, grad_fn=<MeanBackward0>)

不管第1隐藏层输出是什么，$\overline{h_1-\overline{h}_1}=\frac{\sum\limits (h_1-\overline{h}_1)}{\vert h_1\vert}=\frac{\sum h_1-\vert h_1\vert\overline{h_1}}{\vert h_1\vert}=0$ ，即 Y.mean() 应该为0 ，在计算机中表示为一个非常小的数

5.3.2 带参数的层

接受层的输入与输出形状

由于参数在torch中以 Paramater 类封装便于计算，所以在 __init__() 中将参数定义为该类

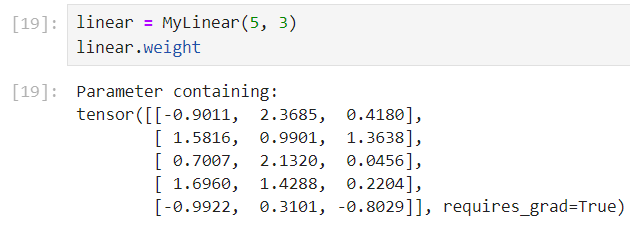
class MyLinear(nn.Module):
    def __init__(self, in_units, units):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(in_units, units))
        self.bias = nn.Parameter(torch.randn(units))
    def forward(self, X):
        linear = torch.matmul(X, self.weight.data) + self.bias.data
        return F.relu(linear)
    
linear = MyLinear(5, 3)
linear.weight

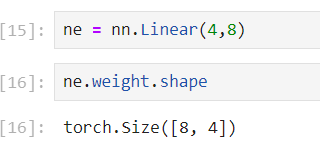
通过 nn.Paramater 实例化自定义参数的形状与定义时相同，即 p=nn.Parameter(torch.randn(5, 3)) ，则 p.shape=torch.Size([5,3])

通过 net=nn.Linear(5,3) 实例化块，其参数 ne.weight.shape=torch.Size([3, 5])

1
2
3

linear(torch.rand(2, 5))
#tensor([[0., 0., 0.],
#        [0., 0., 0.]])

也可以将自定义应用于网络模型构建

net = nn.Sequential(MyLinear(64, 8), MyLinear(8, 1))
net(torch.rand(2, 64))
#tensor([[0.],
#        [0.]])

5.3.3 自定义添加层—net.add()

net.add_module([key],[块声明]) ：向神经网络中添加模块

net.add_module('layer1', nn.Linear(10, 20))

5.4 读写文件

有时我们希望保存训练的模型，以备将来在各种环境中使用（比如在部署中进行预测）。此外，当运行一个耗时较长的训练过程时，最佳的做法是定期保存中间结果，以确保在服务器电源被不小心断掉时，我们不会损失几天的计算结果

5.4.1 加载和保存

对于基本类型：tensor ，tensor[] ，mydict={'a':a,'b':b} 直接调用 torch.load() 和 torch.save() 进行读写，参数为要保存的变量

import torch
from torch import nn
from torch.nn import functional as F

# 张量从内存保存到文件
x = torch.arange(4)
torch.save(x, 'x-file')
# 张量从文件取到内存
x2 = torch.load('x-file')
x2

# 张量列表保存与取回
y = torch.zeros(4)
torch.save([x, y],'x-files')
x2, y2 = torch.load('x-files')

# 张量字典的保存与取回
mydict = {'x': x, 'y': y}
torch.save(mydict, 'mydict')
mydict2 = torch.load('mydict')

5.4.2 保存和加载模型参数

深度学习框架提供了内置函数来保存和加载整个网络

但并不保存整个模型架构，为了恢复模型，我们需要用代码生成架构，然后从磁盘加载参数

class MLP(nn.Module):
    def __init__(self):
        super().__init__()
        self.hidden = nn.Linear(20, 256)
        self.output = nn.Linear(256, 10)

    def forward(self, x):
        return self.output(F.relu(self.hidden(x)))

net = MLP()
X = torch.randn(size=(2, 20))
Y = net(X)

保存参数 ：将模型 state_dict() 输出的参数字典 OrderedDict 实例，保存在 mlp.params 的文件中

1	torch.save(net.state_dict(), 'mlp.params')

恢复模型 ：读取文件，并转换为 OrderedDict 类的实例作为参数

clone = MLP()
clone.load_state_dict(torch.load('mlp.params'))
clone.eval()
#	MLP(
#	  (hidden): Linear(in_features=20, out_features=256, bias=True)
#	  (output): Linear(in_features=256, out_features=10, bias=True)
#	)

5.5 GPU

使用GPU来进行机器学习，因为单个GPU相对运行速度快

1 2	# 查看nvidia驱动程序及CUDA nvidia-smi

在torch中，每个数据都归属于一个设备 (device)，称其为环境（context）。默认情况，所有的变量和计算都分配给CPU

设备间进行数据传输非常不划算 ，在设备（CPU、GPU和其他机器）之间传输数据比计算慢得多。这也使得并行化变得更加困难，因为我们必须等待数据被发送（或者接收），然后才能继续进行更多的操作。

根据经验，多个小操作比一个大操作糟糕得多。此外，一次执行几个操作比代码中散布的许多单个操作要好得多。如果一个设备必须等待另一个设备才能执行其他操作，那么这样的操作可能会阻塞。
当我们打印张量或将张量转换为NumPy格式时，如果数据不在内存中，框架会首先将其复制到内存中，这会导致额外的传输开销。更糟糕的是，它现在受制于全局解释器锁，使得一切都得等待Python完成。

在创建、使用变量是要合理分配环境，最大限度地减少设备间的数据传输时间

5.5.1 设备查看

GPU设备仅代表一个卡和相应的显存，如果有多个 GPU，使用 'cuda:0'，'cuda:1' 分别表示第1块和第2块GPU，'cuda' 默认返回第1块GPU

import torch
from torch import nn

torch.device('cpu'), torch.device('cuda'), torch.device('cuda:1')
#	(device(type='cpu'), device(type='cuda'), device(type='cuda', index=1))

在torch中，通过 torch.device([设备字符串]) 查看在运算时可使用的设备

1 2	# 查看设备数量 torch.cuda.device_count()

5.5.2 设备获取

# 尝试将第i块gpu拿出来返回
def try_gpu(i=0):  #@save
    """如果存在，则返回gpu(i)，否则返回cpu()"""
    if torch.cuda.device_count() >= i + 1:
        return torch.device(f'cuda:{i}')
    return torch.device('cpu')

def try_all_gpus():  #@save
    """返回所有可用的GPU，如果没有GPU，则返回[cpu(),]"""
    devices = [torch.device(f'cuda:{i}') for i in range(torch.cuda.device_count())]
    return devices if devices else [torch.device('cpu')]

try_gpu(), try_gpu(10), try_all_gpus()
#	(device(type='cuda', index=0),
#	 device(type='cpu'),
#	 [device(type='cuda', index=0)])

5.5.3 使用GPU存储变量

1
2
3

x = torch.tensor([1, 2, 3])
x.device
#	device(type='cpu')

可见，不指定设备的前提下，变量默认存储在CPU上

将变量存储在GPU

若对两个张量运算，首先要确定两个张量存储在同一个设备上

创建时指定设备

X = torch.ones(2, 3, device=try_gpu())
X = torch.ones(2, 3, device=try_gpu())
X
#	tensor([[1., 1., 1.],
#	        [1., 1., 1.]], device='cuda:0')

设备间复制

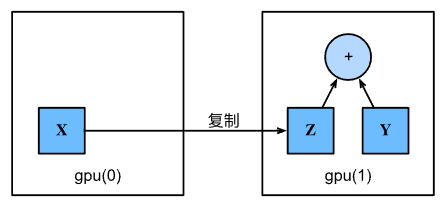
X与Y需要再同一个设备上才可以计算，否则由于在同一设备上找不到数据导致异常。若不在同一GPU上，需要将变量复制到同一GPU上

# 将X移动到GPU 1上作为变量Z
Z = X.cuda(1)
print(X)
print(Z)
#tensor([[1., 1., 1.],
#        [1., 1., 1.]], device='cuda:0')
#tensor([[1., 1., 1.],
#        [1., 1., 1.]], device='cuda:1')

#在GPU1上进行加法
Y + Z

假设变量 Z 已经在第2个GPU上，仍会返回 Z ，并不会复制并分配新内存

神经网络与GPU

神经网络模型也可以指定设备

net = nn.Sequential(nn.Linear(3, 1))
net = net.to(device=try_gpu())

net[0].weight.data.device
# device(type='cuda', index=0)

AmosTian

5.动手学深度学习-pytorch深度计算

5. 深度计算

5.1 层和块

5.1.1 块的概念

5.1.2 pytorc中的块

自定义块

顺序块

块访问

自定义块的特殊用法

层引入常数参数

块组合

5.1.3 操作效率

5.2 参数管理

5.2.1 参数访问

参数类

一次性访问所有参数`net.named_parameters()`

从嵌套块收集参数

5.2.2 参数初始化

预置初始化

自定义初始化

5.2.3 参数共享

5.3 自定义层

5.3.1 不带参数的层

5.3.2 带参数的层

5.3.3 自定义添加层—net.add()

5.4 读写文件

5.4.1 加载和保存

5.4.2 保存和加载模型参数

5.5 GPU

5.5.1 设备查看

5.5.2 设备获取

5.5.3 使用GPU存储变量

将变量存储在GPU

创建时指定设备

设备间复制

神经网络与GPU

5. 深度计算

5.1 层和块

5.1.1 块的概念

5.1.2 pytorc中的块

自定义块

顺序块

块访问

自定义块的特殊用法

层引入常数参数

块组合

5.1.3 操作效率

5.2 参数管理

5.2.1 参数访问

参数类

一次性访问所有参数net.named_parameters()

从嵌套块收集参数

5.2.2 参数初始化

预置初始化

自定义初始化

5.2.3 参数共享

5.3 自定义层

5.3.1 不带参数的层

5.3.2 带参数的层

5.3.3 自定义添加层—net.add()

5.4 读写文件

5.4.1 加载和保存

5.4.2 保存和加载模型参数

5.5 GPU

5.5.1 设备查看

5.5.2 设备获取

5.5.3 使用GPU存储变量

将变量存储在GPU

创建时指定设备

设备间复制

神经网络与GPU

一次性访问所有参数`net.named_parameters()`